PSEB 11th Class Maths Solutions Chapter 16 Probability Ex 16.3

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 16 Probability Ex 16.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 16 Probability Ex 16.3

Question 1.
Which of the following can not be valid assignment of probabilities for outcomes of sample space
S = {ω₁, ω₂, ω₃, ω₄, ω₅, ω₆, ω₇}

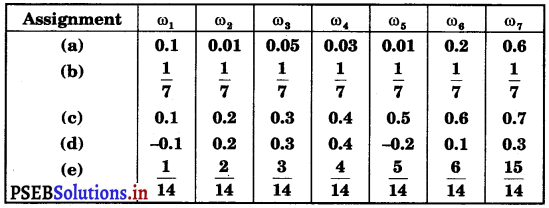
Answer.
(a)

Here, each of the numbers pω₁, is positive and less than 1.
Sum of probabilities = p (ω₁ ) + p (ω₂) + p (ω₃) + p(ω₄) + p (ω₅) + p (ω₆) + p (ω₇)
= 0.1 + 0.01 + 0.05 + 0.03 + 0.01 + 0.2 + 0.6 = 1
Thus, the assignment is valid.

(b)

Here, each of the numbers pea f is positive and less than 1.
Sum of probabilities = p (ω₁ ) + p (ω₂) + p (ω₃) + p(ω₄) + p (ω₅) + p (ω₆) + p (ω₇)
= \(\frac{1}{7}+\frac{1}{7}+\frac{1}{7}+\frac{1}{7}+\frac{1}{7}+\frac{1}{7}+\frac{1}{7}=7 \times \frac{1}{7}\) = 1
Thus, the assignment is valid.

(c)

Sum of probabilities = p (ω₁) + p (ω₂) + p (ω₃) + p(ω₄) + p (ω₅) + p (ω₆) + p (ω₇)
= 0.1 + 0.2 + 0.3 + 0.4 + 0.5 + 0.6 + 0.7 = 2.8 ≠ 1
Thus, the assignment is not valid.

(d)

Here, p(ω₁) and p(ω₂) are negative.
Hence, the assignment is not valid.

(e)

Hence, the assignment is not valid.
p(ω₇) = \(\frac{15}{14}\) > 1.

Question 2.
A coin is tossed twice, what is the probability that atleast one tail occurs?
Answer.
When a coin is tossed twice, the sample space is given by S = (HH, HT, TH, TT}
Let A be the event of the occurrence of atleast one tail.
Accordingly, A – {HT, TH, TT}
∴ P(A) = \(\frac{\text Number of outcomes favourable}{\text { Total number of possible outcomes }}=\frac{n(A)}{n(S)}\)

= \(\frac{3}{4}\)

Question 3.
A die is thrown, find the probability of following events :
(i) A prime number will appear,
(ii) A number greater than or equal to 3 will appear,
(iii) A number less than or equal to one will appear,
(iv) A number more than 6 will appear,
(v) A number less than 6 will appear.
Answer.
The sample space of the given experiment is given by S = {1, 2, 3, 4, 5, 6}
(i) Let A be the event of the occurrence of a prime number. Accordingly, A = {2, 3, 5}
∴ P(A) = \(\frac{\text { Number of outcomes favourable to } A}{\text { Total number of possible outcomes }}=\frac{n(A)}{n(S)}\)

= \(\frac{3}{6}=\frac{1}{2}\)

Let B be the event of the occurrence of a number greater than or equal to 3. Accordingly, B = {3, 4, 5, 6}
∴ P(B) = \(\frac{\text { Number of outcomes favourable to } B}{\text { Total number of possible outcomes }}=\frac{n(A)}{n(S)}\)

= \(\frac{4}{6}=\frac{2}{3}\)

Let C be the event of the occurrence of a number les than or equal to one. Acordingly, C ={1}
∴ P(C) = \(\frac{\text { Number of outcomes favourable to } C}{\text { Total number of possible outcomes }}=\frac{n(C)}{n(S)}\)

= \(\frac{1}{6}\)

Let D be the event of the occurrence of a number greater than 6. Accordingly, D = {} = Φ
∴ P[D) = \(\frac{\text { Number of outcomes favourable to } D}{\text { Total number of possible outcomes }}=\frac{n(D)}{n(S)}\)

= \(\frac{0}{6}\) = 0

Let E be the event of the occurrence of a number less than 6. Accordingly, E = {1, 2, 3, 4, 5}
∴ P(E) = \(\frac{\text { Number of outcomes favourable to } E}{\text { Total number of possible outcomes }}=\frac{n(E)}{n(S)}\)

= \(\frac{5}{6}\).

Question 4.
A card is selected from a pack of 52 cards.
(a) How many points are there in the sample space?
(b) Calculate the probability that the card is an ace of spades.
(c) Calculate the probability that the card is
(i) an ace
(ii) black card.
Answer.
(a) when a card is selected from a pack of 52 cards, the number of possible outcomes is 52 i.e., the sample space contains 52 elements. Therefore there are 52 points in the sample space.

(b) Let A be the event in which the card drawn is an ace of spades. Accordingly, (n)A = 1
∴ P(A) = \(\frac{\text { Number of outcomes favourable to } A}{\text { Total number of possible outcomes }}=\frac{n(A)}{n(S)}\)

= \(\frac{1}{52}\)

(c) (i) Let E be the event in which the card drawn is an ace.
Since there are 4 aces in a pack of 52 cards,
Number of outcomes favourable to E n(E) = 4
∴ P(E) = \(\frac{\text { Number of outcomes favourable to } E}{\text { Total number of possible outcomes }}=\frac{n(E)}{n(S)}\)

= \(\frac{4}{52}=\frac{1}{13}\)

(ii) Let F be the event in which the card drawn is black.
Since there are 26 black cards in a pack of 52 cards, n(F) = 26

∴ P(F) = \(\frac{\text { Number of outcomes favourable to } F}{\text { Total number of possible outcomes }}=\frac{n(F)}{n(S)}\)

= \(\frac{26}{52}=\frac{1}{2}\).

Question 5.
A fair coin wIth 1 marked on one face and 6 on the other and a fair die are both tos,ed. Find the probability that the sum of numbers that turm up is
(i) 3
(ii) 12.
Answer.
Since the fair coin has 1 marked on one face and 6 on the other, and the die has six faces that are numbered 1,2, 3,4, 5, and 6, the sample space is given by
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
Accordingly, n(S) = 12

(i) Let A be the event in which the sum of number that turn up is 3. Accordingly, A = {(1, 2)}
∴ P(A) = \(\frac{\text { Number of outcomes favourable to } A}{\text { Total number of possible outcomes }}=\frac{n(A)}{n(S)}\)

= \(\frac{1}{12}\)

(ii) Let B be the event in which the sum of numbers that turn up is 12. Accordingly, B = {(6, 6)}
∴ P(B) = \(\frac{\text { Number of outcomes favourable to } B}{\text { Total number of possible outcomes }}=\frac{n(B)}{n(S)}\)

= \(\frac{1}{12}\).

Question 6.
There are four men and six women on the city council. If one council member is selected for a committee at random, how likely is it that it is a woman?
Answer.
There are four men and six women on the city council.
As one council member is to be selected for a committee at random, the sample space contains 10 (4 + 6) elements.
Let A be the event in which the selected council member is a woman.
Accordingly, n(A) = 6
∴ P(A) = \(\frac{\text { Number of outcomes favourable to } A}{\text { Total number of possible outcomes }}=\frac{n(A)}{n(S)}\)

= \(\frac{6}{10}=\frac{3}{5}\)

Question 7.
A fair coin is tossed four times, and a person win Re 1 for each head and lose Rs 1.50 for each tail that turns up. From the sample space calculate how many different amounts of money you can have after four tosses and the probability of have each of these amounts.
Answer.
There are five ways in which heads and tails appear.

(i) No head and 4 tail, appear
Money lost = Rs. 4 × 1.50 = Rs. 6.00
There is only 1 way when TTTT occurs.
No. of exhaustive cases = 2⁴ = 16
∴ Probaility of getting no head or 4 tails = \(\frac{1}{16}\).

(ii) When 1 head and 3 tail, appear
Money lost = Rs. (- 1 × 1 + 3 × 1.50) = Rs. 3.50
There are 4 ways when 1 head and 3 tails occur i.e., HTTT, THTT, TTHT, TTTH.
∴ Probaility of getting 1 head and 3 tails = \(\frac{4}{16}=\frac{1}{4}\).

(iii) When 2 head and 2 tail, appear
Money lost = Rs. (2 × 1.5 – 1 × 2) = Rs. (3 – 2) = Re. 1
2 heads and 2 tail may occur as HHTT, HTHT, HTTH, THHT, THTH, TTHH
Thus 2 head and 2 tails may appear in 6 ways
∴ Probability of getting 2 heads and 2 tails = \(\frac{6}{16}=\frac{3}{8}\)

(iv) When 3 head and 1 tail, appear
Money gained Rs. (3 × 1 – 1 × 1.5) = Rs. 1.50
3 heads and 1 tail may occurs as HHHT, HHTH, HTHH, THHH
∴ 3 heads and 1 tail appear in 4 ways
∴ Probability of getting 3 heads and 1 tail = \(\frac{4}{16}=\frac{1}{4}\).

(v) When all the heads appear
Money gained Rs. 4 × 1 = Rs. 4
4 heads occur as HHHH i.e., in one way.
Probability of getting 3 heads = \(\frac{1}{16}\).

Question 8.
Three coins are tossed once. Find the probability of getting
(i) 3 heads
(ii) 2 heads
(iii) at least 2 heads
(iv) at most 2 heads
(v) no head
(vi) 3 tails
(vii) exactly two tails
(viii) no tail
(ix) at most two tails.
Answer.
When three coins are tossed once, the sample space is given by
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
∴ Accordingly, n(S) = 8
It is known that the probability of an event A is given by,
P(A) = \(\frac{\text { Number of outcomes favourable to } A}{\text { Total number of possible outcomes }}=\frac{n(A)}{n(S)}\)

(i) Let B be the event of the occurrence of 3 heads. Accordingly, B={HHH}
∴ P(B) = \(\frac{n(B)}{n(S)}\)

= \(\frac{1}{8}\)

(ii) Let C be the event of the occurrence of 2 heads.
Accordingly, C = {HHT, HTH, THH}
∴ P(C) = \(\frac{n(C)}{n(S)}\)

= \(\frac{3}{8}\)

(iii) Let D be the event of the occurrence of at least 2 heads.
Accordingly, D = {HHH, HHT, HTH, THH}
∴ P(D) = \(\frac{n(D)}{n(S)}\)

= \(\frac{4}{8}=\frac{1}{2}\)

(iv) Let E be the event of the occurrence of almost 2 heads.
Accordingly, E = {HHT, HTH, THH, HTT, THT, TTH, TTT}
∴ P(E) = \(\frac{n(E)}{n(S)}\)

= \(\frac{7}{8}\)

(v) Let F be the event of the occurrence of no head.
Accordingly, F = {TTT}
∴ P(F) = \(\frac{n(F)}{n(S)}\)

= \(\frac{1}{8}\)

(vi) Let G be the event of the occurrence of 3 tails.
Accordingly, G = {TTT}
∴ P(G) = \(\frac{n(G)}{n(S)}\)

= \(\frac{1}{8}\)

(vii) Let H be the event of the occurrence of exacdy 2 tails.
Accordingly, H = {HTT, THT, TTH}
∴ P(H) = \(\frac{n(H)}{n(S)}\)

= \(\frac{3}{8}\)

(viii) Let I be the event of the occurrence of no tail.
Accordingly, I = {HHH}
∴ P(I) = \(\frac{n(I)}{n(S)}\)

= \(\frac{1}{8}\)

(ix) Let J be the event of the occurrence of atmost 2 tails.
Accordingly, J = {HHH, HHT, HTH, THH, HTT, THT, TTH}
∴ P(G) = \(\frac{n(J)}{n(S)}\)

= \(\frac{7}{8}\)

Question 9.
If \(\frac{2}{11}\) is the probability of an event, what is the probability of the event ‘not A’.
Answer.
It is given that P(A) = \(\frac{2}{11}\)
Accordingly, P (not A) = 1 – P(A)
= 1 – \(\frac{2}{11}\) = \(\frac{9}{11}\).

Question 10.
A letter is chosen at random from the word ‘ASSASSINATION’.
Find the probability that letter is (i) a vowel (ii) a consonant.
Answer. There are 13 letters in the word ASSASSINATION.
∴ Hence, n(S) = 13

(i) There are 6 vowels in the given word.
∴ Probability (vowel) = \(\frac{6}{13}\).

(ii) There are 7 consonants in the given word.
∴ Probability (consonant) = \(\frac{7}{13}\).

Question 11.
In a lottery, person choses six different natural numbers at random from 1 to 20, and if these six numbers match with the six numbers airedy fixed by the lottery committee, he wins the prize. What is the probability of winning the prize in the game?
[Hint: order of the numbers is not important.]
Answer.
Total number of ways in which one can choose six different numbers from 1 to 20

= \({ }^{20} C_{6}=\frac{20 !}{6 !(20 !-6 !)}\)

= \(\frac{20 !}{6 ! 14 !}=\frac{20 \times 19 \times 18 \times 17 \times 16 \times 15}{1.2 .3 .4 .5 .6}\)

= 38760

Hence, there are 38760 combinations of 6 numbers.
Out of these combinations, one combination is already fixed by the lottery committee.
Required probability of winning the prize in the game = \(\frac{1}{38760}\).

Question 12.
Check whether the following probabilities P( A) and P(B) are consistently defined
(i) P(A) = 0.5, P(B) = 0.7, P(A ∩ B) = 0.6
(ii) P(A) = 0.5, P(B) = 0.4, P(A ∪ B) = 0.8 ;
Answer.
(i) Here, P(A ∩ B) > P(A)
So, given data is not consistent.

(ii) Here, P(A) = 05, P(B) = 0.4, P(A ∪ B) = 0.8
⇒ P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
⇒ 0.8 = 0.5 + 0.4 – P(A ∩ B)
⇒ P(A ∩ B) = 0.9 – 0.8 = 0.1 < P(A) and P(B)
⇒ P(A) and P(B) are consistent.

Question 13.
Fill in the blanks in following table :

Answer.
(i) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{1}{3}+\frac{1}{5}-\frac{1}{15}\)

= \(\frac{5+3-1}{15}=\frac{7}{15}\)

(ii) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
0.6 = 0.35 + P(B) – 0.25
P(B) = 0.6 – 0.35 + 0.25 = 0.5

(iii) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
0.7 = 0.5 + 0.35 – P(A ∩ B)
P(A ∩ B) = 0.5 + 0.35 – 0.7 = 0.15

Question 14.
Given P(A) = \(\frac{3}{5}\) and P(B) = \(\frac{1}{5}\). Find P(A or B), if A and B are mutually exclusive events.
Answer.
Here, P(A) = \(\frac{3}{5}\), P(B) = \(\frac{1}{5}\)
For mutually exclusive events A and B,
P(A or B) = P(A) + P(B)
∴ P(A or B) = \(\frac{3}{5}\) + \(\frac{1}{5}\) = \(\frac{4}{5}\).

Question 15.
If E and F are events such that P(E) = \(\frac{1}{4}\), P(F) = \(\frac{1}{2}\) and P(E and F) = \(\frac{1}{8}\) find:
(i) P(E or F),
(ii) P (not E and not F).
Answer.
(i) P(E or F) = P(E ∪ F) = P(E) + P(F) – P(E ∩ F)
= \(\frac{1}{4}+\frac{1}{2}-\frac{1}{8}\)

= \(\frac{2+4-1}{8}=\frac{5}{8}\)

(ii) not E and not F = E ∩ F’ = (E ∪ F)’ (De Morgan’s Law)
P(not E and not F) = P(E ∪ F)’
= 1 – P(E ∪ F)
= 1 – \(\frac{5}{8}\) = \(\frac{3}{8}\).

Question 16.
Events E and F are such that P(not E or not F) = 0.25. State whether E and F are mutually exclusive.
Answer.
It is given that P (not E or not F) = 0.25 i.e., P(E ∪ F) = 0.25
⇒ P(E ∪ F)’ = 0.25
[∵ E ∪ F = (E ∩ F)’, De Morgan’s law]
Now, P(E ∩ F) = 1 – P(E ∩ F)’
⇒ P(E ∩ F) = 1 – 0.25
⇒ P(E ∩ F) = 0.75 ≠ 0
⇒ E ∩ F ≠ 0
Thus, E and F are not mutually exclusive.

Question 17.
A and Bare events such that P(A) = 0.42, P(B) = 0.48 and P(A and B) = 0.16. Determine
(i) P(not A),
(ii) P (not B)
(iii) P(A or B).
Answer.
It is given that P(A) = 0.42, P(B) = 0.48, P(A and B) = 0.16
(i) P(not A) = 1 – P(A) = 1 – 0.42 = 0.58
(ii) P(not B) = 1 – P(B) = 1 – 0.48 = 0.52
(iii) We know that P(A or B) = P(A) + P(B) – P(A and B)
P(A or B) = 0.42 + 0.48 – 0.16 = 0.74

Question 18.
In Class XI of a school 40% of the students study Mathematics and 30% study Biology. 10% of the class study both Mathematics and Biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology.
Answer.
Let A be the event in which the selected student studies Mathematics and B be the event in which the selected student studies Biology.
Accordingly, P(A) = 40% = \(\frac{40}{100}=\frac{2}{5}\);

P(B) = 30% = \(\frac{30}{100}=\frac{3}{10}\)

P(A and B) = 10% = \(\frac{10}{100}=\frac{1}{10}\)

We know that P(A or B) = P(A) + P(B) – P(A and B)

∴ P(A or B) = \(\frac{2}{5}+\frac{3}{10}-\frac{1}{10}=\frac{6}{10}\) = 0.6

Thus, the probability that the selected student will be studying mathematics or Biology is 0.6.

Question 19.
In an entrance test that is graded on the basis of two examinations, the probability of a randomly chosen student passing the first examination is 0.8 and the probability of passing the second examination is 0.7. The probability of passing at least one of them is 0.95. What is the probability of passing both?
Answer.
Let A and B be the events of passing the first and second examinations respectively. .
P(A) = 0.8, P(B) = 0.7
Probability of passing at least one examination
= 1 – P(A’ ∩ B’) = 0.95 ……………….(i)
Now A’ ∩ B’ = (A ∪ B)’ (De Morgan’s law)
P(A’ ∩ B) = P(A ∪ B)’= 1 – (A ∪ B)
Putting the value in eQuestion (ii)
1 – [1 – P(A ∪ B)] = 0.95 or P(A ∪ B) = 0.95
Further P(A ∩ B) = P(A) + P(B) – P(A ∪ B)
= 0.8 + 0.7 – 0.95 = 1.5 – 0.95 = 0.55
Thus, probability that the student will pass in both the examinations = 0.55.

Question 20.
The probability that a student will pass the final examination in both English and Hindi is 0.5 and the probability of passing neither is 0.1. If the probability of passing the English examination is 0.75, what is the probability of passing the Hindi examination?
Answer.
Let A and B be the events of passing English and Hindi examinations respectively.
Accordingly, P(A and B) = 0.5, P(not A and not B) = 0.1 i.e.,
P(A’ ∩ B’) = 0.1
P(A)= 0.75
Now, (A ∪ B)’= (A’ ∩ BO [De Morgan’s law]
∴ P(A ∪ B)’ = P(A’ ∩ B’) = 0.1
P(A ∪ B) = 1 – P(A ∪ B)’= 1 – 0.1 = 0.9
We know that P(A or B) = P(A) + P(B) – P(A and B)
∴ 0.9 = 0.75 + P(B) – 0.5
⇒ P(B) = 0.9 – 0.75 + 0.5
⇒ P(B) = 0.65
Thus, the probability of passing the Hindi examination is 0.65.

Question 21.
In a class of 60 students, 30 opted for NCC, 32 opted for NSS and 24 opted for both NCC and NSS. If one of these students is selected at random, find the probability that
(i) The student opted for NCC or NSS.
(ii) The student has opted neither NCC nor NSS.
(iii) The student has opted NSS but not NCC.
Answer.
Let A and B denote the students in NCC and NSS, respectively.
Given, n(A) = 30,
n(B) = 32
n(A ∩ B) = 24,
n(S) = 60 [∵ 24 students opted for both NCC and NSS i.e., they are common in both]

P(A) = \(\frac{30}{60}\) P(B) = \(\frac{32}{60}\) and P(A ∩ B) = \(\frac{24}{60}\)

Then, P(A ∩ B) = \(\frac{2}{12}\)

Now, required probability,
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{6}{12}+\frac{4}{12}-\frac{2}{12}\)

= \(\frac{8}{12}=\frac{2}{3}\)