PSEB 11th Class Maths Solutions Chapter 16 Probability Miscellaneous Exercise

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 16 Probability Ex 16.3 Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 16 Probability Miscellaneous Exercise

Question 1.
A box contains 10 red marbles, 20 blue marbles and 30 green marbles. 5 marbles are drawn from the box, what is the probability that
(i) all will be blue?
(ii) atleast one will be green?
Answer.
The box contains 10 (red) + 20 (blue) + 30 (green)
= 60 marbles of which 5 marbles are drawn.
∴ Total number of outcomes, n(S) = \({ }^{60} C_{5}\)

(i) 5 blue marbles can be drawn from 20 blue marbles in \({ }^{20} C_{5}\) ways.
i.e., n(E₁) = \({ }^{20} C_{5}\)
∴ P (all marbles blue) = \(\frac{n\left(E_{1}\right)}{n(S)}=\frac{{ }^{20} C_{5}}{{ }^{60} C_{5}}\)

= \(\frac{20 \times 19 \times 18 \times 17 \times 16}{60 \times 59 \times 58 \times 57 \times 56}=\frac{34}{11977}\)

(ii) 5 green marbles can be drawn from 30 green marbles in \({ }^{30} C_{5}\) ways i. e.,
n(E₂) = \({ }^{20} C_{5}\)

∴ P (all marbles blue) = \(\frac{n\left(E_{2}\right)}{n(S)}=\frac{{ }^{30} C_{5}}{{ }^{60} C_{5}}\)

P(ar.least one will be green) = 1 – P (5 balls other than green)

= 1 – \(\frac{{ }^{30} C_{5}}{{ }^{60} C_{5}}\)

= 1 – \(\frac{30 \times 29 \times 28 \times 27 \times 26}{60 \times 59 \times 58 \times 57 \times 56}\)

= 1 – \(\frac{117}{4484}\) = \(\frac{4367}{4484}\)

Question 2.
4 cards are drawn from a well-shuffled deck of 52 cards. What is the probability of obtaining 3 diamonds and one spade?
Answer.
Number of ways of drawing 4 cards from 52 cards = \({ }^{52} C_{4}\)
In a deck of 52 cards, there are 13 diamonds and 13 spades.
Number of ways of drawing 3 diamonds and one spade = \({ }^{13} C_{3} \times{ }^{13} C_{1}\)

Thus, the probability of obtaining 3 diamonds and one spade = \(\frac{{ }^{13} C_{3} \times{ }^{13} C_{1}}{{ }^{52} C_{4}}\)

Question 3.
A die has two faces each with number ‘1’, three faces each with number ‘2’ and one face with number ‘3’. If die is rolled once, determine
(i) P(2)
(ii) P(1 or 3)
(iii) P(not 3).
Answer.
Total number of faces = 6
(i) Number faces with number ‘2’ = 3
∴ P(2) = \(\frac{3}{6}=\frac{1}{2}\)

(ii) P (1 or 3) = P (not 2)
= 1 – P(2)
= 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)

(iii) Number of faces with number ‘3’ = 1
∴ P(3) = \(\frac{1}{6}\)
Thus, P(not3) = 1 – P(3)
= 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\).

Question 4.
In a certain lottery, 10,000 tickets are sold and ten equal prizes are awarded. What is the probability of not getting prize if you buy
(a) one ticket
(b) two tickets
(c) 10 tickets?
Answer.
Total number of tickets sold = 10,000
Number of prizes awarded = 10
(i) If we buy one ticket, then
∴ P(getting a prize) = \(\frac{10}{10000}=\frac{1}{1000}\)
∴ P(not getting a prize) = 1 – \(\frac{1}{1000}\)
= \(\frac{999}{1000}\)

(ii) If we buy two tickets, then
Number of tickets, not awarded = 10,000 – 10 = 9990
P(not getting a prize) = \(\frac{{ }^{9990} C_{2}}{{ }^{10000} C_{2}}\)

(iii) If we buy 10 tickets, then
P(not getting a prize) = \(\frac{{ }^{9990} C_{10}}{{ }^{10000} C_{10}}\)

Question 5.
Out of 100 students, two sections of 40 and 60 are formed If you and your friend are among the 100 students, what is the probability that
(a) you both enter the same section?
(b) you both enter the different sections?
Answer.

(a) Let there be two sections A and B of 40 and 60 students, respectively.
∴ 38 students are to selected out of 98, since two particular students are already in section A.
∴ Number of ways of selecting 38 students out of 98 = \({ }^{98} C_{38}\) ways
Number of exhaustive cases of selecting 40 students out of 100 = \({ }^{100} C_{40}\) ways
∴ P(both studensts enter section A) = \(\frac{{ }^{98} C_{38}}{{ }^{100} C_{40}}=\frac{98 !}{38 ! 60 !} \div \frac{100 !}{40 ! 60 !}\)

= \(\frac{98 !}{38 ! 60 !} \times \frac{40 ! 60 !}{100 !}=\frac{40 \times 39}{100 \times 99}=\frac{26}{165}\)

If both students enter the section B. Then, the number of ways of selecting
58 students out of 98 = \({ }^{98} C_{58}\) ways.
Total number of ways of selecting 60 students out of 100 = \({ }^{100} C_{60}\) ways.
∴ Probability that two students enter section
B = \(\frac{{ }^{98} C_{58}}{{ }^{100} C_{60}}=\frac{98 !}{58 ! 40 !} \div \frac{100 !}{60 ! 40 !}\)

= \(\frac{98 !}{58 ! 40 !} \times \frac{60 ! 40 !}{100 !}=\frac{60 \times 59}{100 \times 99}=\frac{59}{165}\)

[∵ \({ }^{n} C_{r}=\frac{n !}{r !(n-r) !}\)]

∴ P (that two particular students enter either section A or B) = \(\frac{26}{165}+\frac{59}{165}=\frac{85}{165}=\frac{17}{33}\)

(b) The probability that they enter different sections
= 1 – P (that two particular students enter either section A or B)

= \(\frac{1}{1}-\frac{17}{33}=\frac{16}{33}\)

Question 6.
Three letters are dictated to three persons and an envelope is addressed to each of them, the letters are inserted into the envelopes at random so that each envelope contains exactly one letter. Find the probability that at least one letter is in its proper envelope
Answer..
Let L₁, L₂, L₃ be three letters and E₁, E₂ and E₃ be their corresponding envelopes respectively.
1 letter in correct envelope and 2 in wrong envelope may be put as

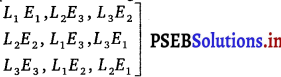
Two lettes or consequently all the letters are in correct envelope may be put in one way.
i.e., (E₁L₁, E₂L₂, E₃L₃)
∴ Number of cases = 3! = 6
Number of favourable cases = 4
Thus, the required probability is \(\frac{4}{6}=\frac{2}{3}\).

Question 7.
A andB are two events such that P(A) = 0.54, P(B) = 0.69 and P (A ∩ B) = 0.35.
Find (i) P (A uP)
(ii) P (A nB)
(iii) P(A nffj
(iv) P (B ∩ A)
Answer.
(i) P(A ∪ B) = P(A) + P(B) – P(A nB)
= 0.54 + 0.69 – 0.35
= 1.23 – 0.35 = 0.88

(ii) A’ ∩ B’ = (A ∪ B)’ By Demorgan’s law.
P(A’ ∩ B’) = P(A ∪ B)’ = 1 – P(A ∪ B)
= 1 – 0.88 = 0.12

(iii) A ∩ B’ = A – A ∩ B
P(A ∩ B’) = P(A) – P(A ∩ B )
= 0.54 – 0.35 = 0.19

(iv) P(B ∩ A’) = P(B) – P (A ∩ B)
= 0.69 – 0.35 = 0.34.

Question 8.
From the employees of a company, 5 persons are selected to represent them in the managing committee of the company. Particulars of five persons are as follows:

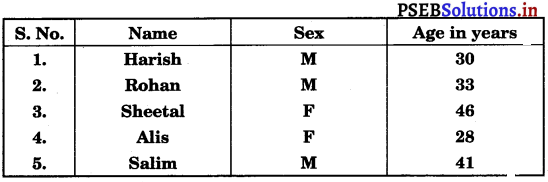
A person is selected at random from this group to act as a spokesperson. What is the probability that the spokesperson will he either male or over 35 years?
Answer.
Let E be the event in which the spokesperson will be a male and F be the event in which the spokesperson will be over 35 years of age.
Accordingly, P(E) = \(\frac{3}{5}\) and P(F) = \(\frac{2}{5}\)
Since there is only one male who is over 35 years of age, P(E ∩ F) = \(\frac{1}{5}\)
We know that P(E ∪ F) = P(E) + P(F) – P(E ∩ F)
∴ P(E ∪ F) = \(\frac{3}{5}+\frac{2}{5}-\frac{1}{5}=\frac{4}{5}\)
Thus, the probability that the spokesperson will either be a male or over 4 35 years of age is \(\frac{4}{5}\).

Question 9.
If 4-digit numbers greater than 5,000 are randomly formed from the digits 0, 1, 3, 5 and 7, what is the probability of forming a number divisible by 5 when,
(i) the digits are repeated?
(ii) the repetition of digits is not allowed?
Answer.
(i) When the digits are repeated Since four-digit numbers greater than 5000 are formed, the leftmost digit is either 7 or 5.
The remaining 3 places can be filled by any of the digits 0, 1, 3, 5 or 7 as repetition of digits is allowed.
∴ Total number of 4-digit numbers greater than 5000 = 2 × 5 × 5 × 5 – 1.
= 250 – 1 = 249.

[In this case, 5000 can not be counted; so 1 is subtracted]
A number is divisible by 5 if the digit at its units place is either O orS.
∴ Total number of 4-digit numbers greater than 5000 that are divisible by 5 = 2 × 5 × 5 × 2 – 1 = 100 – 1 = 99.
Thus, the probability of forming a number divisible by 5 when the digits are repeated is = \(\frac{99}{249}=\frac{33}{83}\).

(ii) When repetition of digits is not allowed
The thousands place can be filled with either of the two digits 5 or 7.
The remaining 3 places can be filled with any of the remaining 4 digits.
∴ Total numbers of 4-digit numbers greater than 5000 = 2 × 4 × 3 × 2 = 48
When the digit at the thousands place is 5, the units place can be filled only with 0 and the tens and hundreds places can be filled with any two of the remaining 3 digits.

∴ Here, number of 4-digit numbers starting with 5 and divisible by 5 = 3 × 2 = 6
When the digit at the thousands place is 7, the units place can be filled in two ways (0 or 5) and the tens and hundreds places can be filled with any two of the remaining 3 digits.
∴ Here, number of 4-digit numbers starting with 7 and divisible by 5 = 1 × 2 × 3 × 2 = 12.
∴ Total number of 4-digit numbers greater than 5000 that are divisible by 5 = 6 + 12 = 18.
Thus, the probability of forming a number divisible by 5 when the repetition of digits is not allowed is \(\frac{18}{48}=\frac{3}{8}\).

Question 10.
The number lock of a suitcase has 4 wheels, each labelled with ten digits i.e., from 0 to 9. The lock opens with a sequence of four digits with no repeats. What is the probability of a person getting the right sequence to open the suitcase?
Answer. When the digits are not repeated, then first place may have one of 10 digits, the second 9, third 8 and fourth 7.
Number of 4-digit numbers, n(S) = 10 × 9 × 8 × 7 = 5040
Now, lock may be opened only in 1 way.
∴ n(E) = 1
∴ Probability of opening the lock = \(\frac{n(E)}{n(S)}=\frac{1}{5040}\).