PSEB 11th Class Maths Solutions Chapter 2 Relations and Functions Miscellaneous Exercise

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 2 Relations and Functions Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 2 Relations and Functions Miscellaneous Exercise

Question 1.
The relation f is defined by f (x) =

The relation g isdefined by g(x) =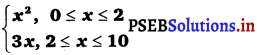
Show that f is a function and g is not a function.
Answer.
The relation f is defined as f (x) =
It is observed that for
0 ≤ x < 3, f(x) = x²
3 ≤ x ≤ 10, f(x) = 3x
Also, at x = 3, f(x) = 3² = 9 or f(x) = 3 × 3 = 9
i.e., at x = 3, f(x) = 9
Therefore, for 0 ≤ x ≤ 10, the images of f(x) are unique.
Thus, the given relation is a function.
The relation g is defined as g (x) =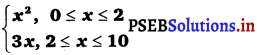
It can be observed that for x = 2, g(x) = 2² = 4 and g(x) = 3 × 2 = 6
Hence, element 2 of the domain of the relation g corresponds to two different images te., 4 and 6. Hence, this relation is not a function.

Question 2.
If f(x) = x², find \(\frac{f(1.1)-f(1)}{(1.1-1)}\).
Ans.
f(x) = x²
∴ \(\frac{f(1.1)-f(1)}{(1.1-1)}\) = \(\frac{(1.1)^{2}-(1)^{2}}{(1.1-1)}=\frac{1.21-1}{0.1}=\frac{0.21}{0.1}\)= 2.1

Question 3.
Find the domain of the function f(x) = \(\frac{x^{2}+2 x+1}{x^{2}-8 x+12}\).
Answer.
The given function is f(x) = \(\frac{x^{2}+2 x+1}{x^{2}-8 x+12}\)

f(x) = \(\frac{x^{2}+2 x+1}{x^{2}-8 x+12}=\frac{x^{2}+2 x+1}{(x-6)(x-2)}\)

It can be seen that function f is defined for all real numbers except at x = 6 and x = 2.
Hence, the domain off is R – {2, 6}.

Question 4.
Find the domain and the renie of the real function f defined by f(x) = \(\sqrt{(x-1)}\).
Answer.
The given real function is f (x) = \(\sqrt{(x-1)}\).
It can be seen that \(\sqrt{(x-1)}\) is defined for (x – 1) ≥ 0.
i.e., f(x) = \(\sqrt{(x-1)}\) is defined for x ≥ 1.
Therefore, the domain off is the set of all real numbers greater than or equal to 1 i.e., the domain of f = [1, ∞).
As x ≥ 1
⇒ (x – 1) ≥ 0
⇒ \(\sqrt{(x-1)}\) ≥ 0
Therefore, the range off is the set of all real numbers greater than or equal to 0 i.e., the range of f = [0, ∞).

Question 5.
Find the domnin and the range of the real function f defined by f(x) = |x – 1|.
Answer.
The given real function isf (x) = |x – 1|.
It is clear that |x – 1| is defined for all real numbers.
∴ Domain of f = R
Also, for x ∈ R, |x – 1| assumes all real numbers.
Hence, the range of f is the set of all non-negative real numbers.

Question 6.
Let f = {(x, \(\frac{x^{2}}{1+x^{2}}\))} : x ∈ R be a function from R into R. Determine the range of f.
Answer.
f = {(x, \(\frac{x^{2}}{1+x^{2}}\))} : x ∈ R

= {(0, 0), (±0.5, \(\frac{1}{5}\)), (±1, \(\frac{1}{2}\)), (±1.5, \(\frac{9}{13}\)), (±2, \(\frac{4}{5}\)), (3, \(\frac{9}{10}\)), (4, \(\frac{16}{17}\))}

The range of f is the set of all second elements. It can be observed that all these elements are greater than or equal to 0 but less than 1, [∵ Denominator is greater than numerator]
Thus, range of f = [0,1).

Question 7.
Let f, g : R → R be defined, respectively by f(x) = x + 1, g(x) = 2x – 3. Find f + g, f – g and \(\frac{f}{g}\).
Answer.
f, g : R → R is defined as f(x) = x + 1, g(x) = 2x – 3
(i) (f + g) (x) = f(x) + g(x)
= (x + 1) + (2x – 3) = 3x – 2
∴ (f + g) (x) = 3x – 2

(ii) (f – g) (x) = f(x) – g(x)
= (x + 1) – (2x – 3)
= x + 1 – 2x + 3 = – x + 4
∴ (f – g) (x) = – x + 4

(iii) \(\frac{f}{g}\) (x) = \(\frac{f(x)}{g(x)}\), g(x) ≠ 0, x ∈ R.

∴ \(\left(\frac{f}{g}\right)(x)=\frac{x+1}{2 x-3}\), 2x – 3 ≠ 0 or 2x ≠ 3

∴ \(\left(\frac{f}{g}\right)(x)=\frac{x+1}{2 x-3}\), x ≠ \(\frac{3}{2}\).

Question 8.
Let f ={(1, 1), (2, 3), (0, – 1), (- 1, – 3)} be a function from Z to Z defined by f(x) = ax + b, for some integers a, b. Determine a, b.
Solution.
f = {(1, 1), (2, 3), (0, – 1), (- 1, – 3)}
f(x) = ax + b
(1, 1) ∈ f
⇒ f (1) = 1
⇒ a × 1 + b = 1
⇒ a + b = 1
(0, – 1) ∈ f
⇒ f (0) = – 1
⇒ a × 0 + b = – 1
⇒ b = – 1
On substituting b= – 1 in a + b = 1, we obtain a + (- 1) = 1
⇒ a = 1 + 1 = 2.
Thus, the respective values of a and b are 2 and – 1.

Question 9.
Let R be a relation from N to N defined by R = {(a, b) : a, b ∈ N and a = b²}. Are the following true?
(i) (a, a) ∈ R, for all a ∈ N
(ii) (a, b) ∈ R, implies (b, a) ∈ R
(iii) (a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R.
Justify your answer in each case.
Answer.
R = {(a, b) : a, b ∈ N and a = b²}
(i) It can be seen that 2 ∈ N; however, 2 ≠ 2² = 4.
Therefore, the statement “(a, a) ∈ R, for all a ∈ N” is not true.

(ii) It can be seen that (9, 3) ∈ N because 9, 3 ∈ N and 9 = 3².
Now, 3 ≠ 9² = 81; therefore, (3, 9) ∈ N
Therefore, the statement “(a, b) ∈ R, implies (b, a) ∈ R is not true.

(iii) It can be seen that (16, 4) ∈ R, (4, 2) ∈ R because 16, 4, 2 e∈ N and 16 = 4² and 4 = 2².
Now, 16 ≠ 2² = 4; therefore, (16, 2) ∈ N
Therefore, the statement “(a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R” is not true.

Question 10.
Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. Are the following true?
(i) f is a relation from A to B
(ii) fis a function from A to B.
Justify your answer in each case.
Answer.
A = {1, 2, 3, 4} and B = {1, 5, 9,11, 15, 16}
∴ A × B = {(1, 1), (1, 5), (1, 9), (1, 11), (1, 15), (1, 16), (2, 1), (2, 5), (2, 9), (2, 11), (2, 15), (2,16), (3, 1), (3, 5), (3, 9),(3, 11),
(3, 15), (3, 16), (4, 1), (4, 5), (4, 9), (4, 11), (4, 15), (4, 16)}
It is given that f = {( 1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}.

(i) A relation from a non-empty set A to a non-empty set B is a subset of the Cartesian product A × B.
It is observed that f is a subset of A × B.
Thus, f is a relation from A to B.
(ii) Since the same first element i.e., 2 corresponds to two different images
i.e., 9 and 11, relation f is not a function.

Question 11.
Let f be the subset of Z × Z defined by f = {(ab, a + b) : a,b ∈ Z}. Is f a function from Z to Z ? Justify your answer.
Answer.
The relation f is defined as f = {(ab, a + b) : a, b ∈ Z}
We know that a relation f from a set A to a set B is said to be a function if every element of set A has unique images in set B.
Since 2, 6, – 2, – 6 ∈ Z, (2 × 6, 2 + 6), (- 2 × – 6, – 2 + (- 6)) ∈ f.
i.e., (12, 8), (12, – 8)
It can be seen that the same first element i.e., 12 corresponds to two different images i.e., 8 and – 8.
Thus, relation f is not a function.

Question 12.
Let A = {9, 10, 11, 12, 13} and let f: A→ N be defined by f(n) = the highest prime factor of n. Find the range of f.
Answer.
A = {9, 10,11, 12, 13}
f : A → N is defined as f(n) = The highest prime factor of n
Prime factor of 9 = 3;
Prime factors of 10 = 2, 5;
Prime factor of 11 = 11;
Prime factors of 12 = 2, 3;
Prime factor of 13 = 13
f(9) = The highest prime factor of 9 = 3
f(10) = The highest prime factor of 10 = 5 .
f(11) = The highest prime factor of 11 = 11
f(12) = The highest prime factor of 12 = 3
f(13) = The highest prime factor of 13 = 13
The range of f is the set of all f(n), where n ∈ A.
∴ Range of f = {3, 5, 11, 13}.