PSEB 11th Class Maths Solutions Chapter 5 Complex Numbers and Quadratic Equations Ex 5.1

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 5 Complex Numbers and Quadratic Equations Ex 5.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations Ex 5.1

Question 1.
Express the given complex number in the form a + ib : (5i) (- \(\frac{3}{5}\) i)
Answer.
(5i) (- \(\frac{3}{5}\) i) = – 5 × \(\frac{3}{5}\) × i × i
= – 3i²
= – 3 (- 1) [∵ i² = – 1]
= 3 + 0 i.

Question 2.
Express the given complex number in the form a + ib : i⁹ + i¹⁹
Answer.
i⁹ + i¹⁹ = i^{4 × 2 + 1} + i^{4 × 4 + 3}
= (i⁴)² . i + (i⁴)⁴ . i³
= 1 × i + 1 × (- i) [∵ i⁴ = i, i³ = – i]
= i + (- i)
= 0 = 0 + 0i.

Question 3.
Express the given complex number in the form a + ib : i³⁹
Answer.

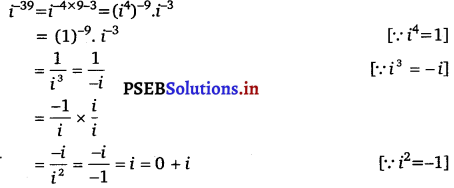
Question 4.
Express the given complex number in the form a + ib : 3 (7 + i7) + i (7 + i7)
Answer.
3 (7 + i7) + i (7 + i7) = 21 + 21i + 7i + 7i²
= 21 + 28i + 7 × (- 1) [∵ i² = – 1]
= 14 + 28i

Question 5.
Express the given complex number in the form
a + ib: (\(\frac{1}{5}+i \frac{2}{5}\)) – (4 + i\(\frac{5}{2}\))
Answer.
(1 – i) – (- 1 + i6) = 1 – i + 1 – 6i
= 2 – 7i.

Question 6.
Express the given complex number in the form \(\left[\left(\frac{1}{3}+i \frac{7}{3}\right)+\left(4+i \frac{1}{3}\right)\right]-\left(-\frac{4}{3}+i\right)\).
Answer.
\(\left(\frac{1}{5}+i \frac{2}{5}\right)-\left(4+i \frac{5}{2}\right)\) = \(\frac{1}{5}+\frac{2}{5} i-4-\frac{5}{2} i\)

= \(\left(\frac{1}{5}-4\right)+i\left(\frac{2}{5}-\frac{5}{2}\right)=\frac{-19}{5}+i\left(\frac{-21}{10}\right)\)

= \(\frac{-19}{5}-\frac{21}{10} i\)

Question 7.
Express the given complex number in the form a + ib : \(\)
Answer.

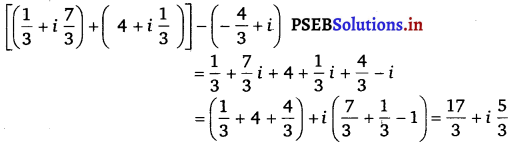
Question 8.
Express the given complex number in the form a + ib : (1 – i)⁴
Answer.
(1 – i)⁴ = [ (1 – i)²]²
= [1² + i² – 2i]²
= [1 -1 – 2i]²
= (- 2i)²
= (- 2i) x (- 2i)
= 4i²  [∵ i² = -1]’
= – 4 = – 4 + 0i.

Question 9.
Express the given complex number in the form a + ib: \(\left(\frac{1}{3}+3 i\right)^{3}[latex].
Answer.

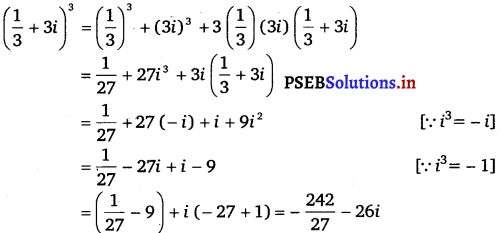
Question 10.
Express the given complex number in the form a + ib = \)\left(-2-\frac{1}{3} i\right)^{3}[/latex]
Answer.
\(\left(-2-\frac{1}{3} i\right)^{3}\) = (- 1)³ \(\left(2+\frac{1}{3} i\right)^{3}\)

= – \(\left[2^{3}+\left(\frac{i}{3}\right)^{3}+3(2)\left(\frac{i}{3}\right)\left(2+\frac{i}{3}\right)\right]\)

Question 11.
Find the multiplicative inverse of the complex number 4 – 3i.
Answer.
Let z = 4 – 3 i,
Then, |z|= \(\sqrt{4^{2}+3^{2}}=\sqrt{16+9}=\sqrt{25}\) = 5
We know that, multiplicative inverse of z
= \(\frac{1}{z}=\frac{\bar{z}}{|z|^{2}}\) [∵ \(\frac{1}{z}=\frac{\bar{z}}{|z|^{2}}\)]

= \(\frac{4+3 i}{(5)^{2}}\) [∵ z = 4 – 3i, \(\overline{\boldsymbol{z}}\) = 4 + 3i]

= \(\frac{4+3 i}{25}=\frac{4}{25}+\frac{3}{25} i\)

Question 12.
Find the multiplicative inverse of the complex number √5 + 3i
Answer.
Let z = √5 + 3i
Then z = √5 – 3i and
|Z|² = (√5)² + 3²
= 5 + 9 = 14
Therefore, the multiplicative inverse of √5 + 3i is given by
z^-1 = \(=\frac{\bar{z}}{|z|^{2}}=\frac{\sqrt{5}-3 i}{14}\)

= \(\frac{\sqrt{5}}{14}-\frac{3 i}{14}\).

Question 13.
Find the multiplicative inverse of the complex number – i.
Answer.
Let z = – i, then, z = i and |z|² = 1² = 1
Therefore, the multiplicative inverse of – i is given by
z^-1 = \(\frac{\bar{z}}{|z|^{2}}=\frac{i}{1}\) = i.

Question 14.
Express the following expression in the form of a + ib = \(\frac{(3+i \sqrt{5})(3-i \sqrt{5})}{(\sqrt{3}+\sqrt{2 i})-(\sqrt{3}-i \sqrt{2})}\).
Answer.