Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 6 Linear Inequalities Miscellaneous Exercise Questions and Answers.
PSEB Solutions for Class 11 Maths Chapter 6 Linear Inequalities Miscellaneous Exercise
Question 1.
Solve the inequality 2 ≤ 3x – 4 < 5.
2 ≤ 3x – 4 < 5
⇒ 2x + 4 < 3x – 4 + 4< 5 + 4
⇒ 6 ≤ 3x ≤ 9
⇒ 2 ≤ x ≤ 3
Thus, all the real numbers x, which are greater than or equal to 2 but less than or equal to 3, are the solutions of the given inequality. The solution set for the given inequality is [2, 3].
Question 2.
Solve the inequality 6 ≤ – 3 (2x – 4) < 12.
Ans.
6 ≤ – 3 (2x – 4) < 12
or \(\frac{6}{3}\) ≤ – 1 (2x – 4) ≤ \(\frac{12}{3}\) [divide by 3]
or 2 ≤ – 1 (2x – 4) ≤ 4
or 2 ≤ (- 2x + 4) ≤ 4
or 2 – 4 ≤ – 2x + 4 – 4 ≤ 4 – 4
or – 2 ≤ – 2x ≤ 0
or \(\frac{-2}{-2} \geq \frac{-2 x}{-2}\) ≥ 0
or 1 ≥ x ≥ 0
Hence, x is less than or equal to 1 and is greater than 0 i.e., x ∈ [0, 1].
![]()
Question 3.
Solve the inequality – 3 ≤ 4 – \(\frac{7 x}{2}\) ≤ 18.
Answer.
– 3 ≤ 4 – \(\frac{7 x}{2}\) ≤ 18
⇒ – 3 – 4 ≤ – \(\frac{7 x}{2}\) ≤ 18 – 4
⇒ – 7 ≤ – \(\frac{7 x}{2}\) ≤ 14
⇒ 7 ≥ \(\frac{7 x}{2}\) ≥ – 14
⇒ 1 ≥ \(\frac{x}{2}\) ≥ – 2
⇒ 2 ≥ x ≥ – 4
Question 4.
Solve the inequality – 15 < \(\frac{3(x-2)}{5}\) ≤ 0.
Answer.
– 15 < \(\frac{3(x-2)}{5}\) ≤ 0
⇒ – 75 < 3 (x – 2) ≤ 0
⇒ – 25 < x – 2 ≤ 0
⇒ – 25 + 2 < x – 2 + 2 ≤ 0 + 2
⇒ – 23 < x ≤ 2
Thus, the solution set for the given inequality is (- 23, 2].
![]()
Question 5.
Solve the inequality – 12 < 4 – \(\frac{3 x}{-5}\) ≤ 2.
Answer.
We have, – 12 < 4 – \(\frac{3 x}{-5}\) ≤ 2

Question 6.
Solve the inequality 7 ≤ \(\frac{(3 x+11)}{2}\) ≤ 11.
Answer.
7 ≤ \(\frac{(3 x+11)}{2}\) ≤ 11
⇒ 14 ≤ 3x + 11 ≤ 22
⇒ 14 – 11 ≤ 3x ≤ 22 – 11
⇒ 3 ≤ 3x ≤ 11
⇒ 1 ≤ x ≤ \(\frac{11}{3}\).
Thus, the solution set for the given inequality is [1, \(\frac{11}{3}\)].
![]()
Question 7.
Solve the inequalities and represent the solution graphically on number line : 5x + 1 > – 24, 5x – 1 < 24.
Answer.
5x + 1 > – 24
5x > – 25
x > -5 …………..(i)
5x – 1 < 24
5x < 25
⇒ x < 5 ……………….(ii)
From inequalities (i) and (ii), it can be concluded that the solution set for the given system of inequalities is (- 5, 5).
The solution of the given system of inequalities can be represented on number line as
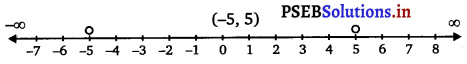
Question 8.
Solve the inequalities and represent the solution graphically on number line:
2(x – 1) < x + 5, 3 (x + 2) > 2x.
Solution.
2(x-l) < x+5
⇒ 2x – 2 < x + 5
⇒ 2x – x < 5 + 2
⇒ x< 7 …………(i) 3(x + 2) > 2 – x
⇒ 3x +6 > 2 – x
⇒ 3x + x > 2 – 6
⇒ 4x > – 4
⇒ x > – 1 ……………..(ii)
From inequalities (i) and (ii), it can be concluded that the solution set for the given system of inequalities is (- 1, 7).
The solution of the given system of inequalities can be represented on number line as
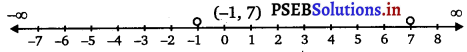
![]()
Question 9.
Solve the following inequalities and represent the solution graphically on number line : 3x – 7 > 2(x – 6), 6 – x > 11 – 2x.
Answer.
3x – 7 > 2 (x – 6)
⇒ 3x – 7 > 2x – 12
⇒ 3x – 2x > – 12 + 7
⇒ x > – 5
6 – x > 11 – 2x
⇒ – x + 2x > 11 – 6
⇒ x > 5 …………….(ii)
From inequalities (i) and (ii), it can be concluded that the solution set for the given system of inequalities is (5, ∞).
The solution of the given system of inequalities can be represented on number line as
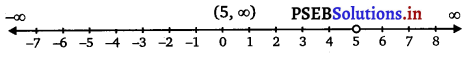
Question 10.
Solve the inequalities and represent the solution graphically on number line : 5 (2x – 7) – 3(2x + 3) < 0, 2x + 19 < 6x + 47.
Answer.
5 (2x – 7) – 3(2x + 3) ≤ 0
⇒ 10x – 35 – 6x – 9 ≤ 0
⇒ 4x – 44 ≤ 0
⇒ 4x ≤ 44
⇒ x ≤ 11 …………….(i)
2x + 19 ≤ 6x + 47
19 – 47 ≤ 6x – 2x
⇒ – 28 < 4x
⇒ – 7 < x …………….(ii)
From inequalities (i) and (ii), it can be concluded that the solution set for the given system of inequalities is [- 7, 11]. The solution of the given system of inequalities can be represented on number line as
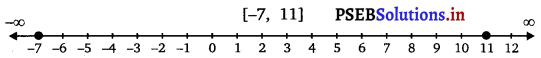
![]()
Question 11.
A solution is to be kept between 68°F and 77°F. What is the range in temperature in degree Celsius (C) if the Celsius/ Fahrenheit (F) conversion formula is given by F = \(\frac{9}{8}\) C + 32 ?
Answer.
Since the solution is to be kept between 68°F and 77°F,
68 < F < 77
Putting F = \(\frac{9}{5}\) C + 32 , we obtain
68 < \(\frac{9}{5}\) C + 32 < 77
⇒ 68 – 32 < \(\frac{9}{5}\) C < 77 – 32
⇒ 36 < \(\frac{9}{5}\) C < 45
⇒ 36 × \(\frac{5}{9}\) < C < 45 × \(\frac{5}{9}\)
⇒ 20 < C < 25
Thus, the required range of temperature in degree Celsius is between 20°C and 25°C.
Question 12.
A solution of 8% boric acid is to be diluted by adding a 2% boric acid solution to it. The resulting mixture is to be more than 4% but less than 6% boric acid. If we have 640 litres of the 8% solution, how many litres of the 2% solution will have to be added?
Answer.
Let x be the number of litres of 2% boric acid solution.
Total mixture = (640 + x) L
∴ According to the question, 2% of x + 8% of 640 > 4% of (640 + x)
⇒ \(\frac{2 x}{100}\) + \(\frac{8}{100}\) × 640 > \(\frac{4}{100}\) (640 + x)
⇒ 2x + 5120 > 2560 + 4x [multiplying both sides by 100]
⇒ 2x + 5120 – 2x > 2560 + 4x – 2x [subtracting 2x from both sides]
⇒ 5120 > 2560 + 2x
⇒ 5120 – 2560 > 2560 + 2x – 2560
⇒ 2560 > 2x
⇒ 2x < 2560
⇒ x < 1280 ………………….(i)
[dividing bothsides by 2]
Also, 2% of x + 8% of 640 < 6% of (640 + x)
⇒ \(\frac{2}{100} \times x+\frac{8}{100} \times 640<\frac{6}{100} \times(640+x)\)
⇒ 2x + 5120 < 3840 + 6x [multiplying both sides by 100]
⇒ 2x + 5120 – 2x < 3840 + 6x – 2x . [subtracting 2x from both sides]
⇒ 5120 < 3840 + 4x
⇒ 5120 – 3840 < 3840 + 4x – 3840 [subtracting 3840 from both sides]
⇒1280 < 4x or 4x > 1280
⇒ \(\frac{4 x}{4}>\frac{1280}{4}\)
⇒ x > 320 ………….(ii)
On combining eqs. (i) and (ii), we get 320 < x < 1280 Thus, the number of litres to be added should be greater than 320 L and less than 1280 L.
![]()
Question 13.
How many litres of water will have to be added to 1125 litres of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content?
Answer.
Let x litres of water is required to be added.
Then,total mixture = (x + 1125) litres.
It is evident that the amount of acid contained in the resulting mixture is 45% of 1125 litres.
This resulting mixture will contain more than 25% but less than 30% acid content.
∴ 30% of (1125 + x) > 45% of 1125
and, 25% of (1125 + x) < 45% of 1125
30% of (1125 + x) > 45% of 1125
\(\frac{30}{100}\) (1125 + x) < \(\frac{45}{100}\) × 1125 ⇒ 30 (1125 + x) > 45 × 1125
⇒ 30 × 1125 + 30x > 45 × 1125
⇒ 30x > 45 × 1125 – 30 × 1125
⇒ 30x > (45 – 30) × 1125
⇒ 30x > 15 × 1125
⇒ x > \(\frac{15 \times 1125}{30}\) = 5625
25% of (1125 + x) < 45% of 1125
⇒ \(\frac{25}{100}\) (1125 + x) < \(\frac{45}{100}\) × 1125
⇒ 25 (1125 + x) < 45 × 1125
⇒ 25 × 1125 + 25x < 45 × 1125
⇒ 25x < 45 × 1125 – 25 × 1125
⇒ 25x < (45 – 25) × 1125
⇒ x < \(\frac{20 \times 1125}{25}\) = 900
∴ 562.5 < x < 900
Thus, the required number of litres of water that is to be added will have to be more than 562.5 litres but less than 900 litres.
![]()
Question 14.
IQ of a person is given by the formula IQ = \(\frac{M A}{C A}\) × 100, where MA is mental age and CA is chronological age. If 80 ≤ IQ ≤ 140 for a group of 12 years old children, find the range of their mental Age.
Ans.
Given, CA = 12 and 80 ≤ IQ ≤ 140 ………………..(i)
Also, IQ = \(\frac{M A}{C A}\) × 100
On putting this value in eq. (i), we get
80 ≤ \(\frac{M A}{C A}\) × 100 ≤ 140
⇒ 80 ≤ \(\frac{M A}{12}\) × 100 ≤ 140 [∵ CA = 12]
⇒ \(\frac{80 \times 12}{100}\) ≤ MA ≤ \(\frac{12}{100}\)
[multiplying bothsides by (\(\frac{12}{100}\))]
⇒ \(\frac{960}{100}\) ≤ MA ≤ \(\frac{1680}{100}\)
⇒ 9.6 ≤ MA ≤ 16.8.
