PSEB 11th Class Maths Solutions Chapter 8 Binomial Theorem Ex 8.1

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 8 Binomial Theorem Ex 8.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 8 Binomial Theorem Ex 8.1

Question 1.
Expand the expression (1 – 2x)⁵.
Answer.
Here, (1 – 2x)⁵ = [1 + (- 2x)]⁵
= \({ }^{5} C_{0}\) + \({ }^{5} C_{1}\) (-2X) + \({ }^{5} C_{2}\) (-2x)2 + \({ }^{5} C_{3}\) (-2x)3 + \({ }^{5} C_{4}\) (-2x)4 + \({ }^{5} C_{5}\) (-2x)s
= 1 + 5 (- 2x) + 10 (4x²) + 10 (- 8x³) + 5(16x⁴) + 1 (- 32x⁵)
= 1 – 10x + 40x² – 80x³ + 80x⁴ – 32x⁵
which is the required expansion.

Question 2.
Expand the expression \(\left(\frac{2}{x}-\frac{x}{2}\right)^{5}\).
Answer.
By using Binomial Theorem, the expression \(\left(\frac{2}{x}-\frac{x}{2}\right)^{5}\) can be expanded as

Question 3.
Expand the expression (2x – 3)⁶.
Answer.
By using Binomial Theorem, the expression (2x – 3)⁶ can be expanded as
(2x – 3) = \({ }^{6} C_{0}\) (2x)⁶ – \({ }^{6} C_{1}\) (2x)⁵ (3) + \({ }^{6} C_{2}\) (2x)⁴ (3)² – \({ }^{6} C_{3}\) (2x)³ (3)³ + \({ }^{6} C_{4}\) (2x)² (3)⁴ – \({ }^{6} C_{5}\) (2x) (3)⁵ + \({ }^{6} C_{6}\) (3)⁶
= 64x⁶ – 6(32x⁵) (3) + (15) (16x⁴) (9) – 20(8x³) (27) + 15(4x²) (81) – 6 (2x) (243) + 729
= 64x⁶ – 576x⁵ + 2160x⁴ – 4320x³ + 4860x² – 2916x + 729

Question 4.
Expand the expression \(\left(\frac{x}{3}+\frac{1}{x}\right)^{5}\).
Answer.
Using Binomial Theorem,

\((a+b)^{n}={ }^{n} C_{0} a^{n}+{ }^{n} C_{1} a^{n-1} b+{ }^{n} C_{2} a^{n-2} b^{2}+\ldots+{ }^{n} C_{n} b^{n}\)

Question 5.
Expand: \(\left(x+\frac{1}{x}\right)^{6}\).
Answer.

Question 6.
Using Binomial Theorem, evaluate (96)³.
Answer.
96 can be expressed as the sum or difference of two numbers whose powers are easier to calculate and then, Binomial Theorem can be applied.
It can be written that, 96 = 100 – 4
∴ (96)³ = (100 – 4)³
= \({ }^{3} C_{0}\) (100)³ – \({ }^{3} C_{1}\) (100)² (4) + \({ }^{3} C_{2}\) (100) (4)² – 3C\({ }^{3} C_{0}\) (4)³
= (100)³ – 3(100)² (4) + 3(100) (4)² – (4)³
= 1000000 – 120000 + 4800 – 64 = 884736.

Question 7.
Using Binomial Theorem, evaluate (102)⁵.
Answer.
102 can be expressed as the sum or difference of two numbers whose powers are easier to calculate and then, Binomial Theorem can be applied.
It can be written that, 102 = 100 + 2
∴ (102)⁵ = (100 + 2)⁵

= \({ }^{5} C_{0}\) (100)⁵ + \({ }^{5} C_{1}\) (100)⁴ (2) + \({ }^{5} C_{2}\) (100)³ (2)² + \({ }^{5} C_{3}\) (100)² (2)³ + \({ }^{5} C_{4}\) (100) (2)⁴ + \({ }^{5} C_{5}\) (2)⁵

= (100)⁵ + 5(100)⁴ (2) + 10 (100)³ (2)² + 10 (100)² (2)³ + 5(100) (2)⁴ + (2)⁵
= 10000000000 + 1000000000 + 40000000 + 800000 + 8000 + 32 = 11040808032

Question 8.
Using Binomial Theorem, evaluate (101)⁴.
Answer.
101 can be expressed as the sum or difference of two numbers whose powers are easier to calculate and then,
Binomial Theorem can be applied.
If can be written that, 101 = 100 + 1
∴ (101)⁴ =(100 + 1)⁴
= \({ }^{4} C_{0}\) (100)⁴ + \({ }^{4} C_{1}\)(100)³ (1) + \({ }^{4} C_{2}\) (100)² (1)² + \({ }^{4} C_{3}\) (100)(1)³ + \({ }^{4} C_{4}\) (1)⁴.

= (100)⁴ + 4(100)³ + 6(100)² + 4(100) + (1)⁴
= 100000000 + 4000000 + 60000 + 400 +1 =104060401.

Question 9.
Using Binomial Theorem, evaluate (99)⁵.
Answer.
99 can be written as the sum or difference of two numbers whose powers are easier to calculate and then, Binomial Theorem can be applied.
It can be written that, 99 = 100 – 1
(99)⁵ =(100 – 1)⁵
= \({ }^{5} C_{0}\) (1oo)⁵ – \({ }^{5} C_{1}\) (100)⁴ (1) + \({ }^{5} C_{2}\) (100)³ (1)² – \({ }^{5} C_{3}\) (100)² (1)³ + \({ }^{5} C_{4}\) (100) (1)⁴ – \({ }^{5} C_{5}\) (1)⁵

= (100)⁵ – 5(100)⁴ + 10(100)³ – 10 (100)² + 5 (100) – 1
= 10000000000 – 500000000 + 10000000 – 100000 + 500 – 1
= 10010000500 – 500100001 = 9509900499.

Question 10.
Using Binomial Theorem, indicate which number is larger (1.1)10000 or 1000.
Answer.
By splitting 1.1 and then applying Binomial Theorem, the first few terms of (1.1)¹⁰⁰⁰⁰ can be obtained as (1.1)¹⁰⁰⁰⁰ = (1 + 0.1)¹⁰⁰⁰⁰
= \({ }^{10000} C_{0}\)+ \({ }^{10000} C_{1}\) (1.1) + Other positive terms
= 1 + 10000 × 1.1 + Other positive terms
= 1 + 11000 + Other positive terms > 1000
Hence, (1.1)¹⁰⁰⁰⁰ > 1000.

Question 11.
Find (a + b)⁴ – (a – b)⁴.
Hence, evaluate (√3 + √2)⁴ – (√3 – √2)⁴.
Answer.
Using Binomial Theorem, the expression, (a + b)⁴ and (a – b)⁴, can be expanded as
(a + b)⁴ = \({ }^{4} C_{0}\) a⁴ + \({ }^{4} C_{1}\)a³b + \({ }^{4} C_{2}\) a²b² + \({ }^{4} C_{3}\) ab³ + \({ }^{4} C_{4}\) b⁴

(a – b)⁴ = \({ }^{4} C_{0}\) a⁴ – \({ }^{4} C_{1}\)a³b + \({ }^{4} C_{2}\) a²b² – \({ }^{4} C_{3}\) ab³ + \({ }^{4} C_{4}\) b⁴

∴ (a + b)⁴ – (a + b)⁴ =
= \({ }^{4} C_{0}\) a⁴ + \({ }^{4} C_{1}\) a³b + \({ }^{4} C_{2}\) a²b² + \({ }^{4} C_{3}\) ab³ + \({ }^{4} C_{4}\) b⁴ – [ \({ }^{4} C_{0}\) a⁴ – \({ }^{4} C_{1}\) a³b + \({ }^{4} C_{2}\) a²b² – \({ }^{4} C_{3}\) ab³ + \({ }^{4} C_{4}\) b⁴]

= 2 (\({ }^{4} C_{1}\) a³b + \({ }^{4} C_{1}\) ab³)
= 2(4a³b + 4ab³)
= 8ab(a² + b²)
By putting a = √3 and b = √2 , we obtain ,
(√3 + √2)⁴ – (√3 – √2)⁴ = 8(√3) (√2) {(√3)² + ((√2)²)
= 8(√6) {3 + 2} = 40√6.

Question 12.
Find (x + 1)⁶ + (x – 1)⁶. Hence or otherwise evaluate (√2 + 1)⁶ + (√2 – 1)⁶.
Answer.
We have,

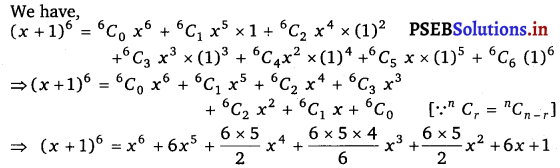
(x + 1)⁶ = x⁶ – 6x⁵ + 15x⁴ + 20x³ + 15x² + 6x + 1 ……………..(i)
Similarly, (x – 1)⁶ = x⁶ – 6x⁵ + 15x⁴ – 20x³ + 15x² – 6x + 1 ………….(ii)
Now, adding eqs. (i) and (ii), we get
(x + 1)⁶ + (x – 1)⁶ = 2 [x⁶ + 15x⁴ + 15x² + 1]
Now, putting x = V2, we get
(√2 + 1)⁶ + (√2 – 1)⁶ = 2[(V2)⁶ +15(V2)⁴ + 15(V2)² + 1]
= 2 [2³ + 15 × 2² + 15 × 2 + 1]
= 2(8 + 15 × 4 + 30 + 1]
= 2 [8 + 60 + 30 + 1]
= 2 [99] = 198.

Question 13.
Show that 9^{N + 1} – 8n – 9 is divisible by 64, whenever n is a positive integer.
Answer.
In order to show that 9^{n + 1} – 8n – 9 is divisible by 64, it has to be proved that,
9^{n + 1} – 8n – 9 = 64k, where k is some natural number.
By Binomial Theorem,

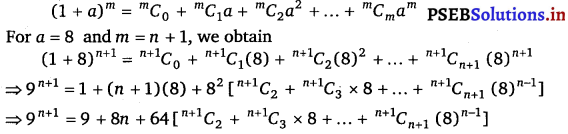
⇒ 9^{n + 1} – 8n – 9 = 64k, where k
= \({ }^{n+1} C_{2}+{ }^{n+1} C_{3} \times 8+\ldots+{ }^{n+1} C_{n+1}(8)^{n-1}\) is a natural number.
Thus, 9^{n + 1} – 8n – 9,is divisible by 64, wherever n is a positive integer.

Question 14.
Prove that \(\sum_{r=0}^{n} \mathbf{3}^{r}{ }^{n} C_{r}\) = 4ⁿ.
Answer.
By Binomial Theorem, \(\sum_{r=0}^{n}{ }^{n} C_{r} a^{n-r} b^{r}\) = (a + b)ⁿ
By putting b = 3^and a = 1 in the above equation, we obtain
\(\sum_{r=0}^{n}{ }^{n} C_{r}(1)^{n-r}(3)^{r}\) = (1 + 3)ⁿ
⇒ \(\sum_{r=0}^{n} 3^{r}{ }^{n} C_{r}\) = 4ⁿ
Hence, proved.