Punjab State Board PSEB 11th Class Physics Important Questions Chapter 6 Work, Energy and Power Important Questions and Answers.
PSEB 11th Class Physics Important Questions Chapter 6 Work, Energy and Powere
Very short answer type questions
Question 1.
Under what condition is the work done by a force inspite of displacement being taking place?
Answer:
Work done by a force is zero inspite of displacement being taking place, if displacement is in a direction perpendicular to that of force applied.
Question 2.
Can acceleration be produced without doing any work? Give example.
Answer:
Yes, for uniform circular motion, no work done but a centripetal acceleration is present.
Question 3.
Does the amount of work done depend upon the fact that how fast is a load raised or moved in the direction of force?
Answer:
The amount of work does not depend upon the fact that how fast is a load raised or moved in the direction of force.
![]()
Question 4.
A body is moving along a circular path. How much work is done by the centripetal force?
Answer:
For a body moving along a circular path, the centripetal force acts along the radius while the displacement is tangential, i. e., θ = 90 °, therefore,
W = Fscos90° = 0.
Question 5.
What is the source of kinetic energy of the bulelt coming out of a rifle?
Answer:
The source of kinetic energy of bullet is the potential energy of the compressed spring in the loaded rifle.
Question 6.
A spring is cut into two equal halves. How is the spring constant of each half affected?
Answer:
Spring constant of each half becomes twice the spring constant of the original spring.
Question 7.
Is collision between two particles possible even without any physical contact between them?
Answer:
Yes, in atomic and subatomic particles collision without any physical contact between the colliding particles is taking place e. g., Rutherford’s alpha particles scattering.
Question 8.
Why is electrical power required at all when the elevator is descending? Why should there be a limit on the number of passengers in this case? (NCERT Exemplar)
Answer:
When the elevator is descending, then electric power is required to prevent it from falling freely under gravity.
Also, as the weight inside the elevator increases, its speed of descending – increases, therefore, there should be a limit on the number of passengers in the elevator to prevent the elevator from descending with large velocity.
![]()
Short answer type questions
Question 1.
A block of mass M is pulled along a horizontal surface by applying a force at an angle θ with horizontal. Coefficient of friction between block and surface is μ. If the block travels with uniform velocity, find the work done by this applied force during a displacement d of the block.
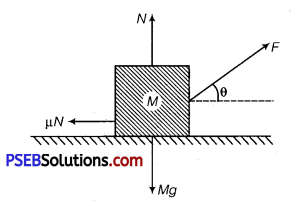
Solution:
The forces acting on the block are shown in figure. As the block moves with uniform velocity the forces add up to zero.
∴ Fcosθ = μN ………….. (i)
Fsinθ + N = Mg ……………. (ii)
Eliminating N from equations (i) and (ii)
F cosθ = μ(Mg – F sinθ)
F = [Latex]\frac{\mu M g}{\cos \theta+\mu \sin \theta}[/Latex]
Work done by this force during a displacement d
W = F. d cosθ = [Latex]\frac{\mu M g d \cos \theta}{\cos \theta+\mu \sin \theta}[/Latex]
Question 2.
Two springs have force constants K2 and K2 (K1 > K2 )• On which spring is more work done when they are stretched by the same force?
Solution:

As x1 < x2
∴ W1 < W2 or W2 > W1
Question 3.
A particle is moving in a circular path of radius r with constant speed. Due to change in the direction of motion of the particle continuously, the velocity of the particle is changing. But the kinetic energy of the particle remains the same. Explain why ?
Solution:
Kinetic energy is given by
E = \(\frac{1}{2}\) mυ2 = \(\frac{1}{2}\) m(\(\vec{v} \cdot \vec{v}\))
Since \(\vec{v} \cdot \vec{v}\) – υ2, a scalar quantity, so it is the speed which is taken into account while calculating the kinetic energy of the particle. As the speed is constant, so kinetic energy of the particle will also remain constant.
![]()
Question 4.
Can a body have energy without momentum? If yes, then explain how they are related with each other?
Solution:
Yes, when p = 0,
Then, K = \(\frac{p^{2}}{2 m}\) = 0
But E = K + U = U (potential energy), which may or may not be zero.
Question 5.
Two bodies A and B having masses mA and mB respectively have equal kinetic energies. If pA and pB are their respective momenta, then prove that the ratio of momenta is equal to the square root of ratio of respective masses.
Solution:
Let υA and υB be the velocities of A and B respectively.
Since their kinetic energies are equal,

Question 6.
Two ball bearings of mass m each, moving in opposite directions with equal speed υ, collide head on with each other. Predict the outcome of the collision, assuming it to be perfectly elastic.
Solution:
Here, m1 = m2 = m
u1 = υ,u2 = -υ
Velocities of two balls after perfectly elastic collision between them are

After collision, the two ball bearings will move with same speeds, but their direction of motion will be reversed.
![]()
Question 7.
An engine is attached to a wagon through a shock absorber of length 1.5 m. The system with a total mass of 50,000 kg is moving with a speed of 36 kmh-1 when the brakes are applied to bring it to rest. In the process of the system being brought to rest, the spring of the shock absorber gets compressed by 1.0 m. If 90% of
energy of the wagon is lost due to friction, calculate the spring constant. (NCERT Exemplar)
Solution:
Given, mass of the system (m) = 50,000 kg
Speed of the system (υ) = 36 km/h
= \(\frac{36 \times 1000}{60 \times 60}\) = 10 m/s
Compression of the spring (x) = 1.0 m
KE of the system = \(\frac{1}{2}\) mυ2 = \(\frac{1}{2}\) × 50000 × (10)2
= 25000 × 100 J = 2.5 × 106J
Since, 90% of KE qf the system is lost due to friction, therefore, energy transferred to shock absorber, is given by
ΔE = \(\frac{1}{2}\)kx2 = 10% of total KE of the system
= \(\frac{10}{100}\) × 2.5 × 106 J or k = \(\frac{2 \times 2.5 \times 10^{6}}{10 \times(1)^{2}}\)
= 5.0 × 106 N/m
Question 8.
An adult weighting 600 N raises the centre of gravity of his body by 0.25 m while taking each step of 1 m length in jogging. If he jogs for 6 km, calculate the energy utilised by him is jogging assuming that there is no energy loss due to friction of ground and air. Assuming that the body of the adult is capable of converting 10% of energy intake in the form of food, calculate the energy equivalents of food that would be required to compensate energy utilised for jogging. (NCERT Exemplar)
Solution:
Given, weight of the adult (w) = mg = 600 N
Height of each step = h = 0.25m
Length of each step = 1 m
Total distance travelled = 6 km = 6000 m
∴ Total number of steps = \(\frac{6000}{1}\) = 6000
Total energy utilised in jogging = n × mgh
= 6000 × 600 × 0.25J = 9 × 105 J
Since, 10% of intake energy is utilised in jogging.
∴ Total intake energy = 10 × 9 × 105J = 9 × 106J
![]()
Long answer type questions
Question 1.
A body of mass 0.3 kg is taken up an inclined plane length 10 m and height 5 m, and then allowed to slide down the bottom again. The coefficient of friction between the body and the plane is 0.15. What is the
(i) work done by gravitational force over the round trip?
(ii) work done by the applied force over the upward journey?
(iii) work done by the frictional force over the round trip?
(iv) kinetic energy of the body at the end of trip? (Take g = 10 ms-2)
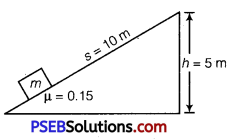
Solution:
Upward journey
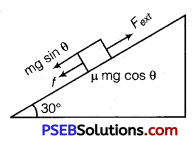
Let us calculate work done by different forces over upward joume Work done by gravitational force
Wi = (mg sinθ)s cos 180°
W 1= 0.3 × 10 sin30° × 10 (-1)
W1 =-15J
Work donp by force of friction
W2 = (μ mg cosθ)s cos180°
W2 = 0.15 × 0.3 × 10 cos30° × 10 (-1)
W2 =-3.879 J
Work done by external force
W3 = Fext × s × cos0°
W3 = [mg sinθ + μ mg cosθ] × 10 × 1
W3 = 18.897 J
Downward journey
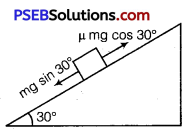
mg sin30°> μ mg cos30°
Work done by the gravitational force
W4 = mg sin 30° × scos0°
W4 = 0.3 × 10 × \(\frac{1}{2}\) × 10 = +15J
Work done by the frictional force
W5 = μmg cos30° × s cos180°
= 0.15 × 0.3 × \(\frac{10 \sqrt{3}}{2}\) × 10 × (-1) = – 3.897 J
(i) Work done by gravitational force over the round trip
= W1 + W4 = 0J
(ii) Work done by applied force over upward journey
= W3 = 18.897J
(iii) Work done by frictional force over the round trip
W2 + W5 = – 3.897 + (-3.897) = – 7.794 J
(iv) Kinetic energy of the body at the end of the trip
W4 + W5 = 11.103 J
![]()
Question 2.
Prove that when a particle suffers an oblique elastic collision with another particle of equal mass anil initially at rest, the two particles would move in mutually perpendicular directions after collisions.
Solution:
Let a particle A of mass m and having velocity u collides with particle B of equal mass but at rest. Let the collision be oblique elastic collision and after collision the particles A and B move with velocities υ1 and υ2 respectively inclined at an angle 0 from each other.
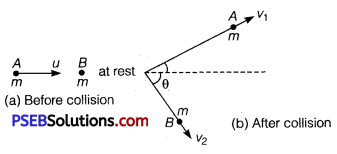
Applying principle of conservation of linear momentum, we get
mu = mυ1 +mυ2 or u = υ1+ υ2
or u2 = (υ1 + υ2) – (υ1 + υ2)
= υ12 + υ22 + 2υ1υ2cos0 ………….. (i)
Again as total KE before collision = Total KE after collision
∴ \(\frac{1}{2}\) mu2 = \(\frac{1}{2}\)mυ12 + \(\frac{1}{2}\)mυ22
⇒ u2 = υ12 + υ22 ……………. (ii)
Comparing eqs. (i) and (ii), we get 2υ1υ2 cosθ = 0
As in an oblique collision both υ1 and υ2 are finite, hence cos0 = 0
⇒ θ = cos-1(0) = \(\frac{\pi}{2}\)
Thus, particles A and B are moving in mutually perpendicular directions after the collision.
