PSEB 12th Class Maths Solutions Chapter 10 Vector Algebra Ex 10.2

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 10 Vector Algebra Ex 10.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 10 Vector Algebra Ex 10.2

Question 1.
Compute the magnitude of the following vectors
\(\overrightarrow{\boldsymbol{a}}=\hat{\boldsymbol{i}}+\hat{\boldsymbol{j}}+\hat{\boldsymbol{k}}\); \(\overrightarrow{\boldsymbol{b}}=\mathbf{2} \hat{\boldsymbol{i}}-\mathbf{7} \hat{j}-\mathbf{3} \hat{\boldsymbol{k}}\); \(\vec{c}=\frac{1}{\sqrt{3}} \hat{i}+\frac{1}{\sqrt{3}} \hat{j}-\frac{1}{\sqrt{3}} \hat{k}\)
Solution.
The given vectors are

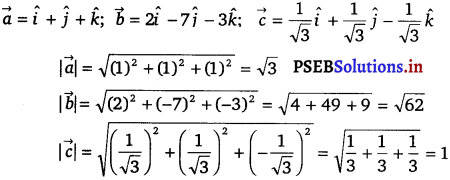
Question 2.
Write two different vectors having same magnitude.
Solution.
Consider the vectors \(\vec{a}=\hat{i}+2 \hat{j}+\hat{k}\) and \(\vec{b}=\hat{i}+\hat{j}+2 \hat{k}\)
\(|\vec{a}|=\sqrt{1^{2}+2^{2}+1^{2}}=\sqrt{6}\),
\([|\vec{b}|=\sqrt{1^{2}+1^{2}+2^{2}}=\sqrt{6}/latex]
Thus, vectors [latex]\vec{a}\) and \(\vec{a}\) have the same magnitude.

Question 3.
Write two different vectors having same direction.
Solution.

The direction cosines of \(\vec{p}\) and \(\vec{q}\) are the same.
Hence, the two vectors have the same direction.

Question 4.
Find the values of x and y so that the vectors \(2 \hat{i}+\mathbf{3} \hat{j}\) and \(x \hat{i}+y \hat{j}\) are equal.
Solution.
The two vectors \(2 \hat{i}+\mathbf{3} \hat{j}\) and \(x \hat{i}+y \hat{j}\) will be equal if their corresponding components are equal.
Hence, the required values of x and y are 2 and 3 respectively.

Question 5.
Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (- 5, 7).
Solution.
The vector with the initial point P(2,1) and terminal point Q(- 5, 7) can be given by,
\(\overline{P Q}=(-5-2) \hat{i}+(7-1) \hat{j}\)

⇒ \(\overline{P Q}=7 \hat{i}+6 \hat{j}\)
Hence, the required scalar components are -7 and 6 while the vector components are – 7î and 6ĵ.

Question 6.
Find the sum of the vectors a = î – 2ĵ + k̂, b = – 2î + 4ĵ + 5k̂ and c = î – 6ĵ – 7k̂.
Solution.
The given vectors are a = î – 2ĵ + k̂, b = – 2î + 4ĵ + 5k̂ and c = î – 6ĵ – 7k̂.
∴ \(\vec{a}+\vec{b}+\vec{c}\) = (1 – 2 + 1) î + (- 2 + 4 – 6) ĵ + (1 + 5 – 7) k̂.
0 . î – 4 ĵ – 1 . k̂ = – 4 ĵ – k̂ .

Question 7.
Find the unit vector in the direction of the vector \(\vec{a}\) = î + ĵ + 2k̂.
Solution.
The unit vector â in the direction of vector \(\vec{a}\) = î + ĵ + 2k̂ is given by

Question 8.
Find the unit vector in the direction of vector \(\overrightarrow{P Q}\), where P and Q are the points (1, 2, 3) and (4, 5, 6), respectively.
Solution.
The given points are P (1, 2, 3) and Q (4, 5 6).

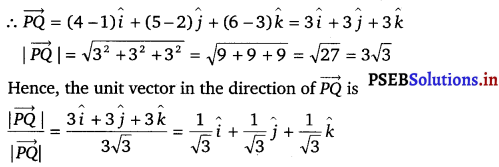
Question 9.
For given vectors, \(\vec{a}\) = 2i – j + 2 k and \(\vec{b}\) = – i + j k, find the unit vector in the direction of the vector \(\vec{a}\) + \(\vec{b}\).
Solution.
The given vectors are \(\vec{a}\) = 2 î – ĵ + 2 k̂ and \(\vec{b}\) = – î + ĵ – k̂
\(\vec{a}\) = 2 î – ĵ + 2 k̂
\(\vec{b}\) = – î + ĵ – k̂
.-. \(\vec{a}\) + \(\vec{a}\) = (2 – 1) î +(- 1 + 1) ĵ + (2 – 1) k̂
= 1 î + 0 ĵ + 1 k̂
|\(\vec{a}\) + \(\vec{b}\)| = \(\sqrt{1^{2}+1^{2}}=\sqrt{2}\)
Hence, the unit vector in the direction of (\(\vec{a}\) + \(\vec{b}\)) is \(\frac{(\vec{a}+\vec{b})}{|\vec{a}-\vec{b}|}=\frac{\hat{i}+\hat{k}}{\sqrt{2}}=\frac{1}{\sqrt{2}} \hat{i}+\frac{1}{\sqrt{2}} \hat{k}\).

Question 10.
Find a vector in the direction of vector 5î – ĵ + 2k̂ which has magnitude 8 units.
Solution.
Let \(\vec{a}\) = – 5î – ĵ + 2k̂
∴ |\(\vec{a}\)| = \(\sqrt{5^{2}+(-1)^{2}+2^{2}}=\sqrt{25+1+4}=\sqrt{30}\)

⇒ \(\hat{a}=\frac{\vec{a}}{|\vec{a}|}=\frac{5 \hat{i}-\hat{j}+2 \hat{k}}{\sqrt{30}}\)

Hence, the vector in the direction of vector 5î – ĵ + 2k̂ which has magnitude 8 units is given by,

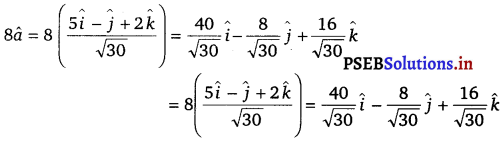
Question 11.
Show that the vectors 2î – 3ĵ + 4k̂ and – 4î + 6ĵ – 8k̂ are collinear.
Solution.
Let \(\vec{a}\) = 2î – 3ĵ + 4k̂ and \(\vec{b}\) = – 4î + 6ĵ – 8k̂.

It is observed that \(\vec{b}\) = – 4î + 6ĵ – 8k̂
= -2 (2î – 3ĵ + 4k̂) = – 2 \(\vec{a}\)
\(\vec{b}\) = λ \(\vec{a}\), where λ = – 2.
Hence, the given vectors are collinear.

Question 12.
Find the direction cosines of the vector î + 2 ĵ + 3 k̂.
Solution.
Let |\(\vec{a}\)| = î + 2 ĵ + 3 k̂
|\(\vec{a}\)| = \(\sqrt{1^{2}+2^{2}+3^{2}}=\sqrt{1+4+9}=\sqrt{14}\)
Hence the direction cosines of \(\vec{a}\) are \(\left(\frac{1}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}}\right)\).

Question 13.
Find the direction cosines of the vector, joining the points A(1, 2,- 3) and B(- 1, – 2, 1) directed from A to B.
Solution.
The given points are A(1, 2, – 3) and B(- 1, – 2, 1).

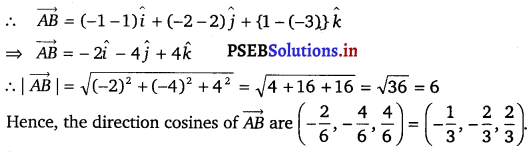
Question 14.
Show that the vector î + ĵ + k̂ is equally inclined to the axes OX, OY and OZ.
Solution.
Let \(\vec{a}\) = î + ĵ + k̂
Then, |\(\vec{a}\)| = \(\sqrt{1^{2}+1^{2}+1^{2}}=\sqrt{3}\)

Therefore, the direction cosines of \(\vec{a}\) are \(\left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right)\).
Now, let α, β and γ be the angles formed by \(\vec{a}\) with the positive directions of x, y and z axes.

Then, we have cos α = \(\frac{1}{\sqrt{3}}\), cos β = \(\frac{1}{\sqrt{3}}\), cos γ = \(\frac{1}{\sqrt{3}}\).

Hence, the given vector is equally inclined to axes OX, OY and OZ.

Question 15.
Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are î + 2ĵ – k̂ and – î + ĵ + k̂ respectively, in the ratio 2 : 1
(i) internally
(ii) externally
Solution.
The position vector of point R dividing the line segment joining two points P and Q in the ratio m : n is given by
Case I:
Internally \(\frac{m \vec{b}+n \vec{a}}{m+n}\)

Case II:
Externally \(\frac{m \vec{b}-n \vec{a}}{m-n}\)
Position vectors of P and Q are given as \(\overrightarrow{O P}\) = î + 2 ĵ – k̂ and \(\overrightarrow{O Q}\) = – î + ĵ + k̂

(i) The position vector of point R which divides the line joining two points P and Q internally in the ratio 2 : 1 is given by
\(\overrightarrow{O R}\) = \(\frac{2(-\hat{i}+\hat{j}+\hat{k})+1(\hat{i}+2 \hat{j}-\hat{k})}{2+1}=\frac{(-2 \hat{i}+2 \hat{j}+2 \hat{k})+(\hat{i}+\hat{j}-\hat{k})}{3}\)

= \(\frac{-\hat{i}+4 \hat{j}+\hat{k}}{3}=-\frac{1}{3} \hat{i}+\frac{4}{3} \hat{j}+\frac{1}{3} \hat{k}\)

The position vector of point R which divides the line joining two points P and Q externally in the ratio 2 : 1 is given by
\(\overrightarrow{O R}\) = \(\frac{2(-\hat{i}+\hat{j}+\hat{k})-1(\hat{i}+2 \hat{j}-\hat{k})}{2-1}\)
= (- 2î + 2ĵ + 2k̂) – (î + 2 ĵ – k̂)
= – 3 î + 3 k̂.

Question 16.
Find the position vector of the mid point of the vector joining the points P( 2, 3, 4) and Q( 4, 1, – 2).
Solution.
The position vector of mid-point R of the vector joining points P(2, 3, 4) and Q(4, 1, – 2) given by
\(\overrightarrow{O R}\) = \(\frac{(2 \hat{i}+3 \hat{j}+4 \hat{k})+(4 \hat{i}+\hat{j}-2 \hat{k})}{2}\)

= \(\frac{(2+4) \hat{i}+(3+1) \hat{j}+(4-2) \hat{k}}{2}\)

= \(\frac{6 \hat{i}+4 \hat{j}+2 \hat{k}}{2}\)

= 3î + 3ĵ + k̂

Question 17.
Show that the points A, B and C with position vectors, a = 3î – 4ĵ – 4k̂, b = 2î – j + k̂ and c = î – 3ĵ – 5k̂, respectively form the vertices of a right angled triangle.
Solution.
Position vectors of points A,B and C are respectively given as

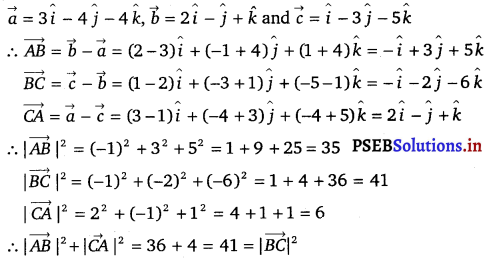
Hence, ABC is a right angled triangle.

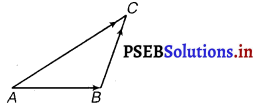
Question 18.
In triangle ABC which of the following is not true

(A) \(\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C A}=\overrightarrow{0}\)
(B) \(\overrightarrow{\boldsymbol{A B}}+\overrightarrow{\boldsymbol{B C}}-\overrightarrow{\boldsymbol{A C}}=\overrightarrow{\mathbf{0}}\)
(C) \(\overrightarrow{\boldsymbol{A B}}+\overrightarrow{B C}-\overrightarrow{C A}=\overrightarrow{0}\)
(D) \(\overrightarrow{\mathbf{A B}}-\overrightarrow{C B}+\overrightarrow{C A}=\overrightarrow{0}\)
Solution.
On applying the triangle law of addition in the given triangle, we have
\(\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}\) ………….(i)

⇒ \(\overrightarrow{A B}+\overrightarrow{B C}=-\overrightarrow{C A}\)

⇒ \(\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C A}=\overrightarrow{0}\) …………(ii)

∴ The equation given in alternative A is true.
\(\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}\)

⇒ \(\overrightarrow{A B}+\overrightarrow{B C}-\overrightarrow{A C}=\overrightarrow{0}\)
∴ The equation given in alternative B is true.
From equation (ii), we have
\(\overrightarrow{A B}-\overrightarrow{C B}+\overrightarrow{C A}=\overrightarrow{0}\)
∴ The equation given in alternative D is true.
Now, consider the equation given in alternative C.
\(\overrightarrow{A B}+\overrightarrow{B C}-\overrightarrow{C A}=\overrightarrow{0}\)

⇒ \(\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{C A}\)………………..(iii)
From equations (i) and (iii), we have AC – CA
⇒ \(\overrightarrow{A C}=\overrightarrow{C A}\)

⇒ \(\overrightarrow{A C}=-\overrightarrow{A C}\)

⇒ \(\overrightarrow{A C}+\overrightarrow{A C}=\overrightarrow{0}\)

⇒ \(2 \overrightarrow{A C}=\overrightarrow{0}\)

⇒ \(\overrightarrow{A C}=\overrightarrow{0}\) which is not true.
Hence, the equation given in alternative C is incorrect.
The correct answer is (C).

Question 19.
If a and B are two collinear vectors, then which of the following are incorrect
(A) \(\overrightarrow{\boldsymbol{b}}\) = X \(\overrightarrow{\boldsymbol{a}}\), for some scalar X
(B) \(\overrightarrow{\boldsymbol{a}}\) = ± \(\overrightarrow{\boldsymbol{b}}\)
(C) The respective components of a and B are proportional
(D) Both the vectors \(\overrightarrow{\boldsymbol{a}}\) and \(\overrightarrow{\boldsymbol{b}}\) have same direction, but different magnitudes.
Solution.

Thus, the respective components of \(\overrightarrow{\boldsymbol{a}}\) and \(\overrightarrow{\boldsymbol{b}}\) are proportional.
However, vector \(\overrightarrow{\boldsymbol{a}}\) and \(\overrightarrow{\boldsymbol{b}}\) can have different directions.
Hence, the statement given in D is incorrect.
The correct answer is (D).