PSEB 12th Class Maths Solutions Chapter 10 Vector Algebra Miscellaneous Exercise

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 10 Vector Algebra Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 10 Vector Algebra Miscellaneous Exercise

Question 1.
Write down a unit vector in XY-plane, making an angle of 30° with the positive direction of tf-axis.
Solution.
Let OP make 30 ° with x-axis, 60 ° with y-axis and 90 ° with z-axis and it lies in XY-plane.
∴ Direction cosines of \(\overrightarrow{O P}\) are cos 30°, cos 60° and cos 90°.

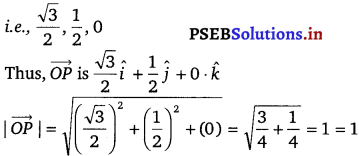
which is required unit vector in XY-plane.

Question 2.
Find the scalar components and magnitude of the vector joining the points P (x₁, y₁, z₁) and Q (x₂, y₂, z₂).
Solution.
The vector joining the points P (x₁, y₁, z₁) and Q (x₂, y₂, z₂) can be obtained by
\(\overrightarrow{P Q}\) = Position vector of Q – Position vector of P
= (x₂ – x₁) î + (y₂ – y₁) ĵ + (z₂ – z₂) k̂

\(|\overrightarrow{P Q}|=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\)

Hence, the scalar components and the magnitude of the vector joining the given points are respectively {(x₂ – x₁), (y₂ – y₁), (z₂ – z₁)} and \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\).

Question 3.
A girl walks 4 km towards west, then she walks 3 km in a direction 30° east of north and stops. Determine the girl’s displacement from her initial point of departure.
Solution.
Let O and B be the initial and final position of the girl respectively.
Then, the girl’s position can be shown as

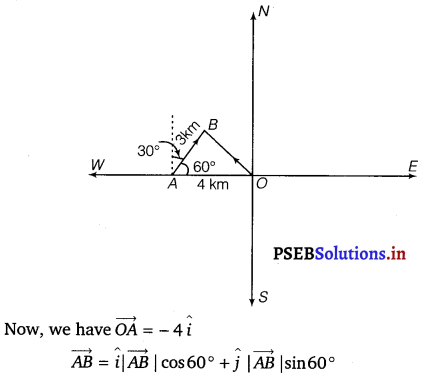
Question 4.
If \(\overrightarrow{\boldsymbol{a}}=\overrightarrow{\boldsymbol{b}}+\overrightarrow{\boldsymbol{c}}\), then is it true that \(|\overrightarrow{\boldsymbol{a}}|=|\overrightarrow{\boldsymbol{b}}|+|\overrightarrow{\boldsymbol{c}}|\)? Justify your answer.
Solution.

Question 5.
Find the value of x for which x (î + ĵ + k̂) is a unit vector.
Solution.

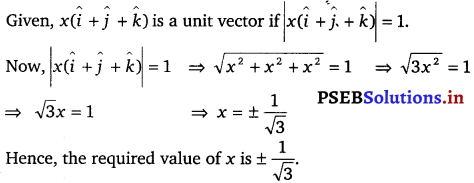
Question 6.
Find a vector of magnitude 5 units and parallel to the resultant of the vectors \(\vec{a}\) = 2 î + 3 ĵ – k̂ and \(\vec{b}\) = î – 2 ĵ + k̂.
Solution.
Given, \(\vec{a}\) = 2 î + 3 ĵ – k̂ and \(\vec{b}\) = î – 2 ĵ + k̂.
Let \(\vec{c}\) be the resultant of \(\vec{a}\) and \(\vec{b}\)
Then, \(\vec{c}\) = \(\vec{a}\) + \(\vec{b}\)
= (2 + 1) î + (3 – 2) ĵ + (- 1 + 1) k̂
= 3 î + ĵ

Question 7.
If \(\vec{a}\) = î + ĵ + k̂, \(\vec{b}\) = 2î – ĵ + 3k̂ and c = î – 2 ĵ + k̂, find a unit vector parallel to the vector 2\(\vec{b}\) – \(\vec{b}\) + 3\(\vec{c}\).
Solution.

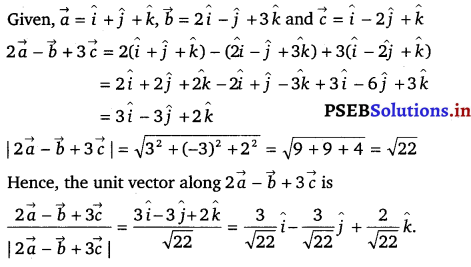
Question 8.
Show that the points A(1, – 2, – 8), B (5, 0, – 2) and C(1, 3, 7) are collinear, and find the ratio in which B divides AC.
Solution.

⇒ 5 (λ + 1)î – 2 (λ + 1)k̂ = (11λ + 1) î + (3λ -2) ĵ + (7λ – 8) k̂
On equating the corresponding components, we get
5(λ + 1) = 11λ + 1
⇒ 5λ + 5 = 11λ +1
⇒ 6λ = 4
⇒ λ = \(\frac{4}{6}=\frac{2}{3}\)
Hence, point B divides AC in the ratio 2 : 3.

Question 9.
Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are (\(2 \vec{a}+\vec{b}\)) and (\(\overrightarrow{\boldsymbol{a}}-\mathbf{3} \vec{b}\)) externally in the ratio 1 : 2. Also, show that P is the mid point of the line segment RQ.
Solution.

Question 10.
The two adjacent sides of a parallelogram are 2î – 4ĵ + 5k̂ and î – 2ĵ – 3k̂. Find the unit vector parallel to its diagonal. Also, find its area.
Solution.

= 22î + 11ĵ
∴ Area of parallelogram = \(\sqrt{(22)^{2}+(11)^{2}}\)
= \(11 \sqrt{4+1}=11 \sqrt{5}\) sq. unit

Thus, the unit vector parallel to its diagonal is \(\frac{1}{7}\) (3î – 6ĵ + 21k̂) and area of parallellogram = 11√5 sq. units.

Question 11.
Show that the direction cosines of a vector equally inclined to the axes, OX, OY and OZ are \(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\).
V3 V3 V3
Let a vector be equally inclined to OX, OY and OZ and let it makes an angle α with each of these three, then, the direction cosines of the vector are cos α, cos α and cos α
Now, cos² α + cos² α + cos² α = 1
⇒ 3 cos² α = 1
⇒ cos α = ± \(\frac{1}{\sqrt{3}}\)
Hence, the direction cosines of the vector which are equally inclined to the axes are either \(\frac{1}{\sqrt{3}}\), \(\frac{1}{\sqrt{3}}\), \(\frac{1}{\sqrt{3}}\) or – \(\frac{1}{\sqrt{3}}\), – \(\frac{1}{\sqrt{3}}\), – \(\frac{1}{\sqrt{3}}\).

Question 12.
Let \(\vec{a}\) = î + 4ĵ + 2k̂, \(\vec{b}\) = 3î – 2ĵ + 7k̂ and \(\vec{c}\) = 2î – ĵ + 4k̂. Find a vector \(\vec{d}\) which is perpendicular to both \(\vec{a}\) and \(\vec{b}\), and \(\overrightarrow{\boldsymbol{c}} \cdot \overrightarrow{\boldsymbol{d}}\) = 15.
Solution.

Question 13.
The scalar product of the vector î + ĵ + k̂ with a unit vector along the sum of vectors 2î + 4ĵ – 5k̂ and λî + 2ĵ + 3k̂ is equal to one. Find the value of λ.
Solution.
(2î + 4ĵ – 5k̂) + (λî + 2ĵ + 3k̂) = (2 + λ)î + 6ĵ – 2k̂

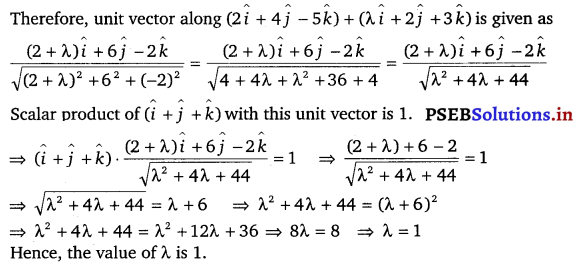
Question 14.
If \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) are mutually perpendicular vectors of equal magnitudes, show that the vector \(\overrightarrow{\boldsymbol{a}}+\overrightarrow{\boldsymbol{b}}+\overrightarrow{\boldsymbol{c}}\) is equally inclined to \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\).
Solution.

Question 15.
Prove that \((\vec{a}+\vec{b}) \cdot(\vec{a}+\vec{b})=|\vec{a}|^{2}+|\vec{b}|^{2}\), if and only if \(\overrightarrow{\boldsymbol{a}}\), \(\overrightarrow{\boldsymbol{b}}\) are perpendicular, given \(\vec{a} \neq \overrightarrow{\mathbf{0}}\), \(\vec{b} \neq \overrightarrow{\mathbf{0}}\).
Solution.

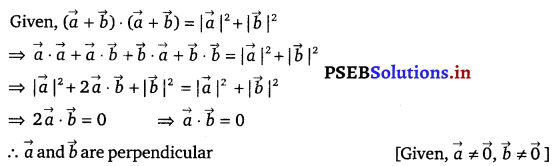
Direction (16 – 19): Choose the correct answer.

Question 16.
If θ is the angle between two vectors \(\vec{a}\) and \(\vec{b}\), then \(\vec{a}\) . \(\vec{b}\) ≥ 0 only when
(A) 0 < θ < \(\frac{\pi}{2}\)
(B) 0 ≤ θ ≤ \(\frac{\pi}{2}\)
(C) 0 < θ < π
(D) 0 ≤ θ ≤ π
Solution.
Let θ be the angle between two vectors \(\vec{a}\) and \(\vec{b}\).
Then, without loss of generality, \(\vec{a}\) and \(\vec{b}\) are non-zero vector so that |\(\vec{a}\)| and |\(\vec{b}\)| are positive.

 

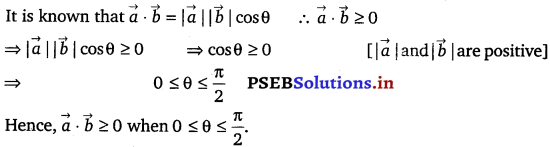
The correct answer is (B).

Question 17.
Let \(\vec{a}\) and \(\vec{b}\) be two unit vectors and 0 is the angle between them. Then \(\vec{a}\) + \(\vec{b}\) is a unit vector if
(A) θ = \(\frac{\pi}{4}\)

(B) θ = \(\frac{\pi}{3}\)

(C) θ = \(\frac{\pi}{2}\)

(D) θ = \(\frac{2 \pi}{3}\)
Solution.
Let \(\vec{a}\) and \(\vec{b}\) be two unit vectors and θ be the angle between them.
Then, |\(\vec{a}\)| = |\(\vec{b}\)| = 1
Now, \(\vec{a}\) + \(\vec{b}\) is a unit vector if |\(\vec{a}\) + \(\vec{b}\)| = 1.

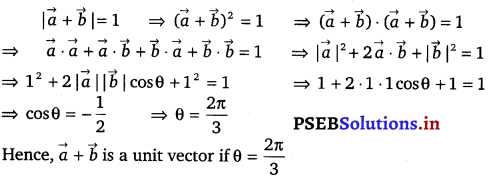
The correct answer is (D).

Question 18.
The value of î (ĵ × k̂) + ĵ . (î × k̂) + k̂. (î × ĵ) is
(A) 0
(B) – 1
(C) 1
(D) 3
Solution.
We have, î (ĵ × k̂) + ĵ . (î × k̂) + k̂. (î × ĵ) = î . î + ĵ . (- ĵ) + k̂ . k̂
= 1 – ĵ . ĵ + 1
= 1 – 1 + 1 = 1
The correct answer is (C).

Question 19.
If θ is the angle between any two vectors \(\overrightarrow{\boldsymbol{a}}\) and \(\overrightarrow{\boldsymbol{b}}\), then |\(\vec{a} \cdot \vec{b}\)| = |\(\overrightarrow{\boldsymbol{a}} \times \overrightarrow{\boldsymbol{b}}\)|, when θ is equal to
(A) 0
(B) \(\frac{\pi}{4}\)
(C) \(\frac{\pi}{2}\)
(D) π
Solution.
Let θ be the angle between two vectors \(\overrightarrow{\boldsymbol{a}}\) and \(\overrightarrow{\boldsymbol{b}}\).
Then, without loss of generality, \(\overrightarrow{\boldsymbol{a}}\) and \(\overrightarrow{\boldsymbol{b}}\) are non-zero vectors, so that |\(\overrightarrow{\boldsymbol{a}}\)| and |\(\overrightarrow{\boldsymbol{b}}\)| are positive.

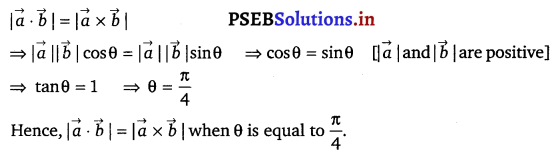
The correct answer is (B).