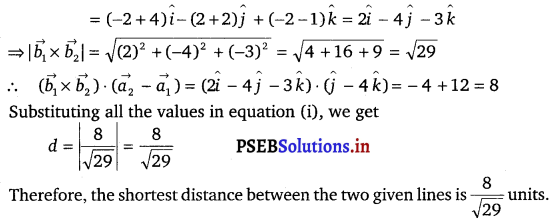PSEB 12th Class Maths Solutions Chapter 11 Three Dimensional Geometry Ex 11.2

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 11 Three Dimensional Geometry Ex 11.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry Ex 11.2

Question 1.
Show that the three lines with direction cosines \(\frac{12}{13}\), \(\frac{-3}{13}\), \(\frac{-4}{13}\); \(\frac{4}{13}\), \(\frac{12}{13}\), \(\frac{3}{13}\); \(\frac{3}{13}\), \(\frac{-4}{13}\), \(\frac{12}{13}\) are mutually perpendicular.
Solution.
Two lines with direction cosines, l₁, m₁, n₁ and l₂ m₂, n₂ are perpendicular to each other, if l₁l₂ + m₁m₂ + n₁n₂ = 0

(i)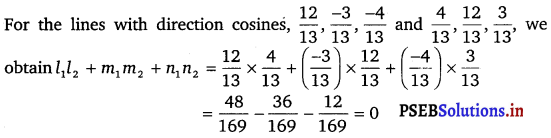

Therefore, the lines are perpendicular.

(ii)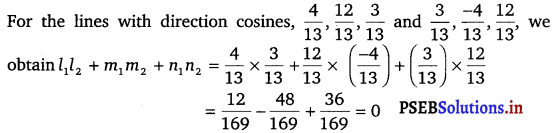

Therefore, the lines are perpendicular.

(iii)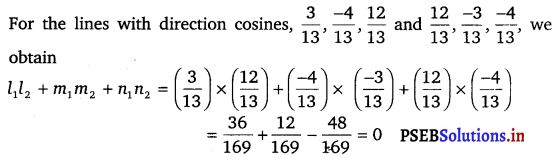
Therefore, the lines are perpendicular.
Thus, all the lines are mutually perpendicular.

Question 2.
Show that the line through the points (1, – 1, 2) (3, 4, – 2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).
Solution.
Let AB be the linejoining the points, (1, – 1, 2)and(3, 4, – 2) and CD be the line joining the points, (0, 3, 2) and (3, 5, 6).
The direction ratios, a₁, b₁, c₁ of AB are (3 – 1), (4 – (- 1)) and (- 2 – 2) i.e., 2, 5 and – 4.
The direction ratios, a₂, b₂, c₂ of CD are (3 – 0), (5 – 3) and (6 – 2 ) i.e., 3, 2 and 4.
AB and CD will be perpendicular to each other, if a₁a₂ + b₁b₂ + c₁c₂ = 0
a₁a₂ + b₁b₂ + c₁c₂ = 2 × 3 + 5 × 2 + (- 4) × 4
= 6 + 10 – 16 = 0
Therefore, AB and CD are perpendicular to each other.

Question 3.
Show that the line through the points (4, 7, 8) (2, 3, 4) is parallel to the line through the points (- 1, – 2, 1), (1, 2, 5).
Solution.
Let AB be the line through the points, (4, 7, 8) and (2, 3, 4) and CD be the line through the points (- 1, – 2, 1) and (1, 2, 5).
The direction ratios a₁, b₁, c₁ of AB are (2 – 4), (3 – 7) and (4 – 8) i.e., – 2, – 4 and – 4.
The direction ratios a₂, b₂, c₂ of CD are (1 – (- 1)), (2 – (- 2)) and (5 – 1) i.e., 2, 4 and 4. .
AB will be parallel to CD, if \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
\(\frac{a_{1}}{a_{2}}=\frac{-2}{2}\) = – 1;

\(\frac{b_{1}}{b_{2}}=\frac{-4}{4}\) = – 1;

\(\frac{c_{1}}{c_{2}}=\frac{-4}{4}\) = – 1

∴ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
Thus, AB is parallel to CD.

Question 4.
Find the equation of the line which passes through the point (1, 2, 3) and is parallel to the vector 3î + 2ĵ – 2k̂.
Solution.
It is given that the line passes through the point A(1, 2, 3).
Therefore, the position vector through A is \(\vec{a}\) = î + 2ĵ + 3k̂, \(\vec{b}\) = 3î + 2ĵ – 2k̂
It is known that the line which passes through point A and parallel to \(\vec{b}\) is given by
\(\vec{r}\) = \(\vec{a}\) + λ \(\vec{b}\), where λ is a constant.
⇒ \(\vec{r}\) = î + 2ĵ + 3k̂ + λ (3î + 2ĵ – 2k̂)
This is the required equation of the line.

Question 5.
Find the equation of the line in vector and in Cartesian form that passes through the point with position vector 2î – ĵ + 4k̂ and is in the direction î + 2ĵ – k̂.
Solution.
It is given that the line passes through the point with position vector
\(\vec{a}\) = 2î – ĵ + 4k̂ ………………….(i)
\(\vec{b}\) = î + 2ĵ – k̂ ………………..(ii)
It is known that a line through a point with position vector a and parallel to b is given by the equation,
\(\vec{r}\) = \(\vec{a}\) + λ \(\vec{b}\)
⇒ \(\vec{r}\) = 2î – ĵ + 4k̂ + λ (î + 2ĵ – k̂)
This is the required equation of the line is vector form.
\(\vec{r}\) = xî – yĵ + zk̂
\(\vec{r}\) = xî – yĵ + zk̂ = (λ + 2)î + (2λ – 1)ĵ + (- λ + 4) k̂
Eliminating λ, we obtain the Cartesian form equation as
\(\frac{x-2}{1}=\frac{y+1}{2}=\frac{z-4}{-1}\)
This is the required equation of the given line in Cartesian form.

Question 6.
Find the Cartesian equation of the line which passes through the point (- 2, 4, – 5) and parallel to the line given by
\(\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}\).
Solution.
It is given that the line passes through the point (- 2, 4, – 5) and is parallel to \(\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}\)

The direction ratios of the line, \(\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}\), are 3, 5 and 6.

The required line is parallel to \(\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}\)

Therefore, its direction ratios are 3k, 5k and 6k where k ≠ 0.

It is known that the equation of the line through the point (x₁, y₁, z₁) and with direction ratios, a, b, c is given by \(\frac{x-x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}\).

Therefore, the equation of the required line is \(\frac{x+2}{3 k}=\frac{y-4}{5 k}=\frac{z+5}{6 k}\)

\(\frac{x+2}{3}=\frac{y-4}{5}=\frac{z+5}{6}\) = k

Question 7.
The Cartesian equation of a line is \(\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}\). Write its vector form.
Solution.
The Cartesian equation of a line is \(\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}\) …………..(i)
The given line passes through the point (5, – 4, 6).
The position vector of this point is \(\vec{a}\) = 5î – 4ĵ + 6k̂
Also, the direction ratios of the given line are 3, 7 and 2.
This means that the line is in the direction of vector, \(\vec{b}\) = 3î + 7ĵ + 2k̂
It is known that the line through position vector \(\vec{a}\) and in the direction of the vector \(\vec{b}\) is given by the equation,
\(\vec{r}\) = \(\vec{a}\) + λ \(\vec{b}\), λ ∈ R
=*> r = (5î – 4ĵ + 6k̂) + λ (3î + 7ĵ + 2k̂)
This is the required equation of the given line in vector form.

Question 8.
Find the vector and the Cartesian equations of the lines that passes through the origin and (5, – 2, 3).
Solution.
The required line passes through the origin.
Therefore, its position vector is given by,
\(\vec{a}=\overrightarrow{0}\) …………..(i)
The direction ratios of the line through origin and (5, – 2, 3) are
(5 – 0) = 5 (- 2 – 0) = – 2 (3 – 0) = 3
The line is parallel to the vector given by the equation, \(\vec{b}\) = 5î – 2ĵ+ 3k̂
The equation of the line in vector form through a point with position vector \(\vec{a}\) and parallel to \(\vec{b}\) is,
\(\vec{r}\) = \(\vec{a}\) + λ \(\vec{b}\), λ ∈ R
⇒ \(\vec{r}\) = \(\vec{0}\) + λ (5î – 2ĵ+ 3k̂)
⇒ \(\vec{r}\) = λ (5î – 2ĵ+ 3k̂)

The equation of the line through the point (x₁, y₁, z₁) and direction ratios a, b, c is given by, \(\frac{x-x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}\)

Therefore, the equation of the required line in the Cartesian form is
\(\frac{x-0}{5}=\frac{y-0}{-2}=\frac{z-0}{3}\)

⇒ \(\frac{x}{5}=\frac{y}{-2}=\frac{z}{3}\)

Question 9.
Find the vector and the Cartesian equations of the line that passes through the points (3, – 2, – 5), (3, – 2, 6).
Solution.
Let the line passing through the points, P(3, – 2, – 5) and Q(3, – 2, 6), be PQ.
Since PQ passes through P(3, – 2, – 5), its position vector is given by
\(\vec{a}\) = 3î – 2ĵ – 5k̂
The direction ratios of PQ are given by,
(3 – 3) = 0, (- 2 + 2) = 0, (6 + 5) = 11
The equation of the vector in the direction of PQ is
\(\vec{b}\) = 0î – 0ĵ + k̂ = 11k̂
The equation of PQ in vector form is given by,
\(\vec{r}\) = \(\vec{a}\) + λ \(\vec{b}\), λ ∈ R
⇒ \(\vec{r}\) = (3î – 2ĵ – 5k̂) + 11λk̂
The equation of PQ in Cartesian form is
\(\frac{x-x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}\) i.e.,

\(\frac{x-3}{0}=\frac{y+2}{0}=\frac{z+5}{11}\)

Question 10.
Find the angle between the following pairs of lines
(i) \(\vec{r}\) = 2î – 5ĵ + k̂ + λ (3î + 2ĵ + 6k̂) and
\(\vec{r}\) = 7î – 6k̂ + µ (î + 2ĵ + 2k̂)

(ii) \(\vec{r}\) = 3î + ĵ – 2k̂ + λ (î – ĵ – 2k̂) and
r = 2î – ĵ – 56k̂ + µ (3î – 5ĵ – 4k̂)
Solution.
(i) Let Q be the angle between the given lines.
The angle between the given pairs of lines is given by, cos θ
The given lines are parallel to the vectors, \(\vec{b}_{1}\) = 3î + 2ĵ+ 6k̂ and \(\vec{b}_{2}\) = î + 2ĵ + 2k̂ respectively.
∴ \(\left|\vec{b}_{1}\right|=\sqrt{3^{2}+2^{2}+6^{2}}\) = 7;

\(\left|\vec{b}_{2}\right|=\sqrt{(1)^{2}+(2)^{2}+(2)^{2}}\) = 3.

\(\vec{b}_{1}\) . \(\vec{b}_{2}\) = (3î + 2ĵ+ 6k̂) . (î + 2ĵ + 2k̂)
= 3 × 1 + 2 × 2 + 6 × 2
= 3 + 4 + 12 = 19
⇒ cos θ = \(\\left|\frac{\overrightarrow{b_{1}} \cdot \overrightarrow{b_{2}}}{\mid \overrightarrow{b_{1}} \| \vec{b}_{2}}\right|\)

θ = cos^-1 \(\left(\frac{19}{21}\right)\)

(ii) The given lines are parallel to the vectors \(\vec{b}_{1}\) = î – ĵ – 2k̂ and \(\vec{b}_{2}\) = 3î – 5ĵ – 4k̂, respectively.

Question 11.
Find the angle between the following pair of lines
(i) \(\frac{x-2}{2}=\frac{y-1}{5}=\frac{z+3}{-3}\) and \(\frac{x+2}{-1}=\frac{y-4}{8}=\frac{z-5}{4}\)

(ii) \(\frac{x}{2}=\frac{y}{2}=\frac{z}{1}\) and \(\frac{x-5}{4}=\frac{y-2}{1}=\frac{z-3}{8}\)
Solution.

⇒ cos θ = \(\frac{26}{9 \sqrt{38}}\)

θ = cos^-1 \(\left(\frac{26}{9 \sqrt{38}}\right)\)

(ii)

Question 12.
Find the values of p so that the lines \(\frac{1-x}{3}=\frac{7 y-14}{2 p}=\frac{z-3}{2}\) and \(\frac{7-7 x}{3 p}=\frac{y-5}{1}=\frac{6-z}{5}\) are at right angles.
Solution.
The given equations are not in the standard form.
The equations of the given lines can be written as
\(\) …………….(i)

and \(\) ……………..(ii)

The direction ratios of the given lines are – 3, \(\frac{2 p}{7}\), 2 and \(-\frac{3 p}{7}\), 1, – 5.
Two lines with direction ratios a₁, b₁, c₁ and a₂, b₂, c₂ are perpendicular to each other, if
a₁ a₂ + b₁b₂ + c₁c₂ = 0
∴ (- 3) (\(-\frac{3 p}{7}\)) + (\(\frac{2 p}{7}\)) (1) + (2) – (5) = 0
⇒ 9p + 2p – 70 = 0
⇒ 11p = 70
⇒ p = \(-\frac{70}{11}\)

Question 13.
Show that the lines \(\frac{x-5}{7}=\frac{y+2}{-5}=\frac{z}{1}\) and \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}\) are perpendicular to each other.
Solution.
The equations of the given lines are \(\frac{x-5}{7}=\frac{y+2}{-5}=\frac{z}{1}\) and \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}\).

The direction ratios of the given lines are 7, – 5, 1 and 1, 2, 3 respectively.

Two lines with direction ratios, a₁, b₁, c₁ and a₂, b₂, c₂ are perpendicular to each other, if
a₁a₂ + b₁b₂ + c₁c₂ = 0
∴ 7 × 1 + (- 5) × 2 + 1 × 3
= 7 – 10 + 3 = 0
Therefore, the given lines are perpendicular to each other.

Question 14.
Find the shortest distance between the lines \(\overrightarrow{\boldsymbol{r}}\) = (î + 2ĵ + k̂) + λ (î – ĵ + k̂) and \(\overrightarrow{\boldsymbol{r}}\) = 2î – ĵ – k̂ + μ (2î + ĵ + 2k̂).
Solution.
The equations of the given lines are \(\overrightarrow{\boldsymbol{r}}\) = (î + 2ĵ + k̂) + λ (î – ĵ + k̂) and \(\overrightarrow{\boldsymbol{r}}\) = 2î – ĵ – k̂ + μ (2î + ĵ + 2k̂).
It is known that the shortest distance between the lines, \(\vec{r}\) = \(\vec{a}_{1}\) + λ \(\vec{b}_{1}\) and \(\vec{r}\) = \(\vec{a}_{2}\) + λ \(\vec{b}_{2}\) is given by
d = \(\left|\frac{\left(\overrightarrow{b_{1}} \times \vec{b}_{2}\right) \cdot\left(\overrightarrow{a_{2}}-\overrightarrow{a_{2}}\right)}{\left|\overrightarrow{b_{1}} \times \overrightarrow{b_{2}}\right|}\right|\) ……………….(i)

Compare the given equations, we get

Question 15.
Find the shortest distance between the lines \(\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1}\) and \(\frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}\).
Solution.

Question 16.
Find the shortest distance between the lines whose vector equations are \(\vec{r}\) = (î + 2ĵ + 3k̂) + λ (î – 3ĵ + 2k̂) and \(\vec{r}\) = 4î + 5ĵ + 6k̂ + µ (2î+ 3ĵ + k̂)
Solution.

Question 17.
Find the shortest distance between the lines whose vector equations are \(\overrightarrow{\boldsymbol{r}}\) = (1 – t) î + (t- 2) ĵ + (3 – 21) k̂ and \(\overrightarrow{\boldsymbol{r}}\) = (s + 1) î + (2s – 1) ĵ – (2s + 1) k̂.
Solution.
The given lines are \(\overrightarrow{\boldsymbol{r}}\) = (1 – t) î + (t – 2) ĵ + (3 – 2t) k̂
\(\vec{r}\) = (î – 2ĵ + 3 k̂) +1(- î + ĵ – 2 k̂) …………(i)
\(\vec{r}\) = (s + 1) î + (2s – 1) ĵ – (2s + 1) k̂
\(\vec{r}\) = (î – ĵ + k̂) + s (î + 2ĵ – 2k̂) …………(ii)