Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 13 Probability Ex 13.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 12 Maths Chapter 13 Probability Ex 13.1
Question 1.
Given that E and F are events such that P(E) = 0.6, P(F) = 0.3 and P(E ∩ F) = 0.2, find P(E/F) and P(F/E).
Solution.
It is given that, P(E) = 0.6, P(F) = 0.3 and P(E ∩ F) = 0.2
⇒ P(E/F) = \(\frac{P(E \cap F)}{P(F)}=\frac{0.2}{0.3}=\frac{2}{3}\)
and P(F/E) = \(\frac{P(E \cap F)}{P(E)}=\frac{0.2}{0.6}=\frac{1}{3}\)
Question 2.
Compute P(A/B), if P(B) 0.5 and P(A ∩ B) = 0.32.
Solution.
It is given that, P(B) = 0.5 and P(A ∩ B)= 0.32
⇒ P(A/B) = \(\frac{P(A \cap B)}{P(B)}=\frac{0.32}{0.5}=\frac{16}{25}\).
![]()
Question 3.
If P(A) = 0.8, P(B)= 0.5 and P(B/A)= 0.4, find
(i) P(AB)
(ii) P(A/B)
(iii) P(A ∪ B)
Solution.
k is given that, P(A) = 0.8, P(B) 0.5 and P(B/A) = 0.4
(i) P(B|A) = 0.4
∴ \(\frac{P(A \cap B)}{P(A)}\) = 0.4
⇒ \(\frac{P(A \cap B)}{0.8}\) = 0.4
⇒ P(A ∩ B) = 0.32
(ii) P (A/B) = \(\frac{P(A \cap B)}{P(B)}\)
⇒ P(A/B) = \(\frac{0.32}{0.5}\) = 0.64
(iii) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
⇒ P(A ∪ B) = 0.8 + 0.5 – 0.32 = 0.98
Question 4.
Evaluate P(A ∪ B), if 2P(A) = P(B) = \(\frac{5}{13}\) and P(A/B) = \(\frac{2}{5}\).
Solution.
It is given that, 2P(A) = P(B) = \(\frac{5}{13}\)
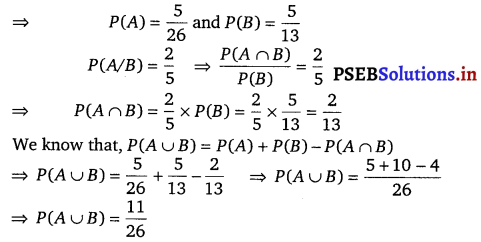
![]()
Question 5.
If P(A) = \(\frac{6}{11}\), P(B) = \(\frac{5}{11}\) and P(A uB) = \(\frac{7}{11}\), find
(i) P(A ∩ B)
(ii) P(A/B)
(iii) P(B/A)
Solution.

Direction (6 – 9): Determine P(E/F):
Question 6.
A coin is tossed three times, where
(i) E : head on third toss, F : heads on first two tosses.
(ii) E : at least two heads, F : at most two heads
(iii) E : at most two tails, F : at least on tail
Solution.
When a coin is tossed three times, then the sample space S is
S = {HHH, HHT, HTH, HIT, THH, THT, TTH, TTT}
It, can be seen that the sample space has 8 elements.
(i) E = {HHH, HTH, THH, TTH}
F = {HHH, HHT}
∴ E ∩ F = {HHH}
P(F) = \(\frac{2}{8}=\frac{1}{4}\) and P(E ∩ F) = \(\frac{1}{8}\)
P(E/F) = \(\frac{P(E \cap F)}{P(F)}=\frac{\frac{1}{8}}{\frac{1}{4}}=\frac{4}{8}=\frac{1}{2}\)
(ii) E = {HHH, HHT, HTH, THH}
F = {HHT, HTH, HTT, THH, THT, TTH, TTT}
∴ E ∩ F – {HHT, HTH, THH}
Clearly, P(E ∩ F) = \(\frac{3}{8}\) and P(F) = \(\frac{7}{8}\)
P(E/F) = \(\frac{P(E \cap F)}{P(F)}=\frac{\frac{3}{8}}{\frac{7}{8}}=\frac{3}{7}\)
(iii) E = {HHH, HHT, HTT, HTH, THH, THT, TTH}
F = {HHT, HTT, HTH, THH, THT TTH, TTT}
∴ E ∩ F = {HHT, HTT, HTH, THH, THT, TTH} v
P(F) = \(\frac{7}{8}\) and P(E ∩ F) = \(\frac{6}{8}\)
Therefore, P(E/F) = \(\frac{P(E \cap F)}{P(F)}=\frac{\frac{6}{8}}{\frac{7}{8}}=\frac{6}{7}\)
![]()
Question 7.
Two coins are tossed once, where
(i) E : tail appears on one coin, F : one coin shows head
(ii) E : no tail appears, F : no head appears
Solution.
If two coins are tossed once, then the sample space S is,
S = {HH, HT, TH, TT}
E : tail appears on one coin – {TH, HT}
F : one coin shows head = {HT, TH}
E ∩ F : {TH, HT}
∴ P(E ∩ F) = \(\frac{2}{4}=\frac{1}{2}\),
P(F) = \(\frac{2}{4}=\frac{1}{2}\)
P(E/F) = \(\frac{P(E \cap F)}{P(F)}=\frac{1 / 2}{1 / 2}\) = 1
(ii) E = set of events having no tail = {HH}
F = set of events having no head = {TT} and E ∩ F = Φ
P(F) = 1 and P(E ∩ F) = 0
∴ P(E / F) = \(\frac{P(E \cap F)}{P(F)}=\frac{0}{1}\) = 0
Question 8.
A die is thrown three times,
E : 4 appears on the third toss, F : 6 and 5 appears respectively on first two tosses.
Solution.
If a die is thrown three times, then the number of elements in the sample space will be 6 × 6 × 6 = 216

and F = {(6, 5, 1) (6, 5, 2), (6, 5, 3) (6, 5, 4) (6, 5, 5), (6, 5, 6)}
∴ E ∩ F = {(6, 5, 4)}
P(F) = \(\frac{6}{216}\) and P(E ∩ F) = \(\frac{1}{216}\)
[∵ From three dice, number of exhaustive cases = 6 × 6 × 6 = 216]
∴ P(E/F) = \(\frac{P(E \cap F)}{P(F)}=\frac{\frac{1}{216}}{\frac{6}{216}}=\frac{1}{6}\)
![]()
Question 9.
Mother, father and son line up at random for a family picture
E : son on one end, F : father in middle.
Solution.
If mother (M), father (P), and son (S) line up for family picture, then the sample space will be
S = {MFS, MSF, FMS, FSM, SMF, SFM}
⇒ E = {MFS, FMS, SMF, SFM}
F = {MFS, SFM}
E ∩ F = {MFS, SFM}
P(E ∩ F) = \(\frac{2}{6}=\frac{1}{3}\)
P(F) = \(\frac{2}{6}=\frac{1}{3}\)
P(E/F) = \(\frac{P(E \cap F)}{P(F)}=\frac{1 / 3}{1 / 3}\) = 1
Question 10.
A black and a red dice are rolled.
(a) Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5.
(b) Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.
Solution.
Let the first observation be from the black die and second from the red die.
When two dice (one black and another red) are rolled the sample space S has 6 × 6 = 36 number of elements
(a) Let
A : Obtaining a sum greater than 9 = {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)
B : Black die results in a 5 = {(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}
∴ A ∩ B = {(5, 5), (5, 6)}
The conditional probability of obtaining a sum is greater than 9, given that the black die resulted in a 5 is given by P(A/B).
∴ P(A/B) = \(\frac{P(A \cap B)}{P(B)}=\frac{\frac{2}{36}}{\frac{6}{36}}=\frac{2}{6}=\frac{1}{3}\)
(b) E : Sum of the observations is 8 = {2, 6), (3, 5), (4, 4), (5, 3), (6, 2)}
F : Red die resulted in a number less than 4
= 
⇒ E ∩ F – {(5, 3), (6, 2)}
Similarly, P(F) = \(\frac{18}{36}\) and P(E ∩ F) = \(\frac{2}{36}=\frac{1}{18}\)
The conditional probability of obtaining the sum equal to 8 given that the red die resulted in a number less then 4 is given by P(E/F).
Therefore, P(E/F) = \(\frac{P(E \cap F)}{P(F)}=\frac{\frac{2}{36}}{\frac{18}{36}}=\frac{2}{18}=\frac{1}{9}\).
![]()
Question 11.
A fair die is rolled. Consider events E = {1, 3, 5}, F (2, 3) and G = {2, 3, 4, 5}. Find
(i) P(E/F) and P(F/E)
(ii) P(E/G) and P(G/E)
(iii) P((E ∪ F)/G) and P((E ∩ F)/G)
Solution.
When a fair die is rolled, the sample space S will be S = {1, 2, 3, 4, 5, 6}
(i) 
(ii) E ∩ G = {3, 5}

(iii) E ∪ F = {1, 2, 3, 5}
(E ∪ F) ∩ G = {12, 3, 5} ∩ {2, 3, 4, 5} = {2, 3, 5} £ ∩ F = {3}
(E ∩ F) ∩ G = {3} ∩ {2, 3, 4, 5} = {3}
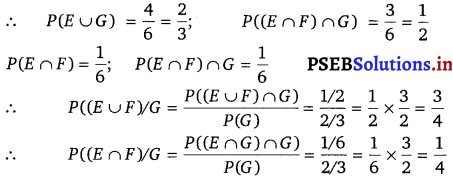
![]()
Question 12.
Assume that each horn child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls given that
(i) the youngest is a girl,
(ii) at least one is a girl?
Solution.
Let b and g represent the boy and the girl child respectively. If a family has two children, the sample space will be
S = {(b, b), (b, g), (g, b), (g, g)}
Let A be the event that both children are girls.
∴ A = {(g, g)}
(i) Let B be the event that the youngest child is a girl.
B = [(b, g), (g, g)] =$
⇒ A ∩ B = {(g, g)}
⇒ P(B) = \(\frac{2}{4}=\frac{1}{2}\) and P(A ∩ B) = \(\frac{1}{4}\)
The conditional probability that both are girls, given that the youngest child is a girl, is given by P(A/B).
P(A/B) = \(\frac{P(A \cap B)}{P(B)}=\frac{\frac{1}{4}}{\frac{1}{2}}=\frac{1}{2}\)
Therefore, the required probability is \(\frac{1}{2}\).
(ii) Let C be the event that at least one child is a girl.
∴ C = {(b, g), (g, b)(g, g)}
⇒ A ∩ C = {g, g}
⇒ P(C) = \(\frac{3}{4}\) and P(A ∩ C) = \(\frac{1}{4}\).
The conditional probability that both are girls, given that at least one child is a girl, is given by P(A/C).
Therefore, P(A/C) = \(\frac{P(A \cap C)}{P(C)}=\frac{\frac{1}{4}}{\frac{3}{4}}=\frac{1}{3}\).
![]()
Question 13.
An instructor has a question bank consisting of 300 easy True/False questions, 200 difficult True/False questions, 500 easy multiple choice questions and 400 difficult multiple choice questions. If a question is selected at random from the question?
Solution.
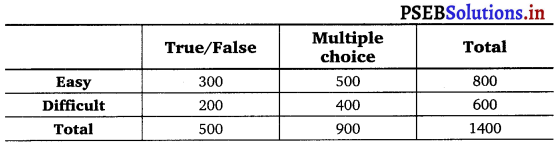
Let us denote E = easy questions, M = multiple choice questions, D =
difficult questions, and T = True/False questions
Total number of questions = 1400
Total number of multiple choice questions = 900
Therefore, probability of selecting an easy multiple choice questions is
P(E ∩ M) = \(\frac{500}{1400}=\frac{5}{14}\)
Probability of selecting a multiple choice questions, P(M) is
\(\frac{900}{1400}=\frac{9}{14}\)
Therefore, the required probability is \(\frac{5}{9}\).
![]()
Question 14.
Given that the two numbers appearing on throwing the two dice are different. Find the probability of the event, “the sum of numbers on the dice is 4”.
Solution.
When dice is thrown, number of observations in the sample space = 6 × 6 = 36
Let A be the event that the sum of the numbers on the dice is 4 and B be the event that the two numbers appearing on throwing the two dice are different.

P(B) = \(\frac{30}{36}=\frac{5}{6}\) and
P(A ∩ B) = \(\frac{2}{36}=\frac{1}{18}\)
Let P(A/B) represent the probability that the sum of the numbers on the dice is 4, given that the two numbers appearing on throwing the two dice are different.
∴ P(A/B) = \(\frac{P(A \cap B)}{P(B)}=\frac{\frac{1}{18}}{\frac{5}{6}}=\frac{1}{15}\)
Therefore, the required probability is \(\frac{1}{15}\).
Question 15.
Consider the experiment of throwing a die, if a multiple of 3 comes up, throw the die again and if any other number comes, toss a coin. Find the conditional probability of the event ‘the coin shows a tail’, given that ‘at least one die shows a 3’.
Solution.
The outcomes of the given experiment can be represented by the following set.
The sample space of the experiment is,

Direction (16 – 17): Choose the correct answer.
Question 16.
If P(A) = \(\frac{1}{2}\), P(B) = 0, then P(A/B) is
(A) 0
(B) \(\frac{1}{2}\)
(C) not defined
(D) 1
Solution.
It is given that P(A) = \(\frac{1}{2}\) and P(B) = 0
P(A/B) = \(\frac{P(A \cap B)}{P(B)}=\frac{P(A \cap B)}{0}=\infty\)
Therefore, P(A/B) is not defined.
Thus, the correct answer is (C).
Question 17.
If A and B are events such that P(A/B) = P(B/A), then
(A) A ⊂ B but A±B
(B) A = B
(C) A ∩ B = Φ
(D) P(A) = P(B)
Solution.
It is given that, P(A/B) = P(B/A)
⇒ \(\frac{P(A \cap B)}{P(B)}=\frac{P(A \cap B)}{P(A)}\)
⇒ P(B) = P(A).
Thus, the correct answer is (D).
