Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 2 Inverse Trigonometric Functions Ex 2.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions Ex 2.2
Direction (1 – 4): Prove the following.
Question 1.
3 sin-1 x = sin-1 (3x – 4x3), x ∈ [- \(\frac{1}{2}\), \(\frac{1}{2}\)]
Solution.
Let x = sin θ. Then, sin-1 x = θ.
We have,
R.H.S. = sin-1 (3x – 4x3) = sin-1(3 sin θ – 4 sin3 θ)
= sin-1 (sin 3θ) = 3θ = 3 sin-1 x
= L.H.S.
Hence proved.
![]()
Question 2.
3 cos-1 x = cos-1 (4x3 – 3x), x ∈ [\(\frac{1}{2}\), 1]
Solution.
Let x = cos θ. Then, cos-1 x = θ.
We have, R.H.S. = cos-1 (4x3 – 3x)
= cos-1 (4cos 3θ – 3 cos θ)
= cos-1 (cos 3θ) = 3θ = 3 cos-1 x
= L.H.S.
Hence proved.
Question 3.
tan-1 \(\frac{2}{11}\) + tan-1 \(\frac{7}{24}\) = tan-1 \(\frac{1}{2}\).
Solution.
Given, tan-1 \(\frac{2}{11}\) + tan-1 \(\frac{7}{24}\) = tan-1 \(\frac{1}{2}\)

![]()
Question 4.
2 tan-1 \(\frac{1}{2}\) + tan-1 \(\frac{1}{7}\) = tan-1 \(\frac{31}{17}\)
Solution.
Given, 2 tan-1 \(\frac{1}{2}\) + tan-1 \(\frac{1}{7}\) = tan-1 \(\frac{31}{17}\)
L.H.S. = 2 tan-1 \(\frac{1}{2}\) + tan-1 \(\frac{1}{7}\)
= \(\tan ^{-1}\left[\frac{2 \cdot \frac{1}{2}}{1-\left(\frac{1}{2}\right)^{2}}\right]+\tan ^{-1}\left(\frac{1}{7}\right)\) [∵ 2 tan-1 x = tan-1 (\(\frac{2 x}{1-x^{2}}\))]

Direction (5 – 10):- Write the following functions in the simplest form:
Question 5.
tan-1 \(\frac{\sqrt{1+x^{2}}-1}{x}\), x ≠ 0.
Solution.
We have, tan-1 \(\frac{\sqrt{1+x^{2}}-1}{x}\)
put x = tan θ
⇒ θ = tan-1 x

![]()
Question 6.
tan-1 \(\frac{1}{\sqrt{x^{2}-1}}\), |x| > 1
Solution.
Let x = sec θ, then θ = sec-1 x
∴ tan-1 \(\frac{1}{\sqrt{x^{2}-1}}\) = tan-1 \(\left(\frac{1}{\sqrt{\sec ^{2} \theta-1}}\right)\)
= tan-1 \(\left(\frac{1}{\sqrt{\tan ^{2} \theta}}\right)\) [∵ sec2 θ – 1 = tan2 θ]
= tan-1 \(\left(\frac{1}{\tan \theta}\right)\)
= tan-1 (cot θ)
= tan-1 [tan (\(\frac{\pi}{2}\) – θ)] [∵ tan (\(\frac{\pi}{2}\) – θ) = cot θ]
= \(\frac{\pi}{2}\) – θ
= \(\frac{\pi}{2}\) – sec-1 x
Question 7.
tan-1 \(\left(\sqrt{\frac{1-\cos x}{1+\cos x}}\right)\), x < π.
Solution.
We have, tan-1 \(\left(\sqrt{\frac{1-\cos x}{1+\cos x}}\right)\)
= tan-1 \(\left(\sqrt{\frac{2 \sin ^{2} \frac{x}{2}}{2 \cos ^{2} \frac{x}{2}}}\right)\)
= tan-1 (tan \(\left(\frac{\sin \frac{x}{2}}{\cos \frac{x}{2}}\right)\))
= tan-1 (tan \(\frac{x}{2}\))
= \(\frac{x}{2}\).
![]()
Question 8.
tan-1 (\(\frac{\cos x-\sin x}{\cos x+\sin x}\)), 0 < x < π.
Solution.
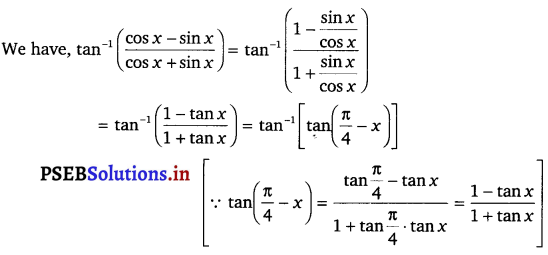
Question 9.
tan-1 \(\frac{x}{\sqrt{a^{2}-x^{2}}}\), |x| < a.
Solution.
We have, tan-1 \(\frac{x}{\sqrt{a^{2}-x^{2}}}\)
Let x = a sin θ
⇒ \(\frac{x}{a}\) = sin θ
⇒ θ = sin-1 (\(\frac{x}{a}\))
∴ tan-1 \(\frac{x}{\sqrt{a^{2}-x^{2}}}\) = tan-1 \(\left(\frac{a \sin \theta}{\sqrt{a^{2}-a^{2} \sin ^{2} \theta}}\right)\)
= tan-1 \(\left(\frac{a \sin \theta}{a \sqrt{1-\sin ^{2} \theta}}\right)\)
= tan-1 \(\left(\frac{a \sin \theta}{a \cos \theta}\right)\)
= tan-1 (tan θ)
= θ = sin-1 \(\frac{x}{a}\).
![]()
Question 10.
tan-1 \(\left(\frac{3 a^{2} x-x^{3}}{a^{3}-3 a x^{2}}\right)\), a > 0; \(\frac{-a}{\sqrt{3}} \leq x \leq \frac{a}{\sqrt{3}}\).
Solution.
We have, tan-1 \(\left(\frac{3 a^{2} x-x^{3}}{a^{3}-3 a x^{2}}\right)\), a > 0; \(\frac{-a}{\sqrt{3}} \leq x \leq \frac{a}{\sqrt{3}}\)
Let x = a tan θ
⇒ \(\frac{x}{a}\) = tan θ
⇒ θ = tan-1 \(\frac{x}{a}\)
∴ tan-1 \(\left(\frac{3 a^{2} x-x^{3}}{a^{3}-3 a x^{2}}\right)\), a > 0; \(\frac{-a}{\sqrt{3}} \leq x \leq \frac{a}{\sqrt{3}}\) = tan-1 \(\left(\frac{3 a^{2} \cdot(a \tan \theta)-a^{3} \tan ^{3} \theta}{a^{3}-3 a \cdot\left(a^{2} \tan ^{2} \theta\right)}\right)\)
= tan -1 \(\left(\frac{3 a^{3} \tan \theta-a^{3} \tan ^{3} \theta}{a^{3}-3 a^{3} \tan ^{2} \theta}\right)\)
= tan-1 \(\left(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\right)\)
= tan-1 (tan 3θ) [∵ tan 3θ = \(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\)]
= 3θ = 3 tan-1 \(\frac{x}{a}\).
Direction (11 – 15) : Find the value of each of the following.
Question 11.
tan-1 [2 cos(2 sin-1 \(\frac{1}{2}\))].
Solution.
Let sin-1 \(\frac{1}{2}\) = x
Then, sin x = \(\frac{1}{2}\) = sin (\(\frac{\pi}{6}\)))
Now, tan-1 [2 cos(2 sin-1 \(\frac{1}{2}\))] = tan-1 [2 cos(2 × \(\frac{\pi}{6}\))]
= tan-1 [2 cos \(\frac{\pi}{3}\)]
= tan-1 [2 × \(\frac{1}{2}\)] [∵ cos (\(\frac{\pi}{3}\)) = \(\frac{1}{2}\))
= tan-1 1 = \(\frac{\pi}{4}\).
![]()
Question 12.
cot(tan-1 a + cot-1 a).
Solution.
We have, cot(tan-1 a + cot-1 a)
= cot (\(\frac{\pi}{2}\))
= 0 [∵ tan-1 x + cot-1 x = \(\frac{\pi}{2}\)]
Question 13.
tan \(\frac{1}{2}\) [sin-1 \(\frac{2 x}{1+x^{2}}\) + cos-1 \(\frac{1-y^{2}}{1+y^{2}}\)], |x| < 1, y > 0 and xy < 1.
Solution.
Let x = tan θ.
Then, θ = tan-1 x.
∴ sin-1 \(\frac{2 x}{1+x^{2}}\) = sin-1 \(\left(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right)\)
= sin-1 (sin 2θ) = 2θ = 2 tan-1 x
Again, let y = tan φ.
Then, φ = tan-1 y
∴ cos-1 \(\frac{1-y^{2}}{1+y^{2}}\) = cos-1 \(\left(\frac{1-\tan ^{2} \varphi}{1+\tan ^{2} \varphi}\right)\)
= cos-1 (cos 2φ) = 2φ = 2 tan-1 y
Now, tan \(\frac{1}{2}\) [sin-1 \(\frac{2 x}{1+x^{2}}\) + cos-1 \(\frac{1-y^{2}}{1+y^{2}}\)]
= tan \(\frac{1}{2}\) [2 tan-1 x + tan-1 y]
= tan [tan-1 x + tan-1 y]
= tan[tan-1 \(\left(\frac{x+y}{1-x y}\right)\)]
[∵ tan-1 x + tan-1 y = tan-1 \(\left(\frac{x+y}{1-x y}\right)\)]
= \(\frac{x+y}{1-x y}\)
![]()
Question 14.
If sin(sin-1 \(\frac{1}{5}\) + cos-1 x) = 1, then find the value of x.
Solution.
Given, sin(sin-1 \(\frac{1}{5}\) + cos-1 x) = 1
⇒ sin-1 \(\frac{1}{5}\) + cos-1 x = sin-1 (1)
[∵ sin θ = x ⇒ θ = sin-1 x]
⇒ sin-1 \(\frac{1}{5}\) + cos-1 x = sin-1 (sin \(\frac{\pi}{2}\))
[∵ sin (\(\frac{\pi}{2}\)) = 1]
⇒ sin-1 \(\frac{1}{5}\) + cos-1 x = \(\frac{\pi}{2}\)
⇒ sin-1 \(\frac{1}{5}\) = \(\frac{\pi}{2}\) – cos-1 x
sin-1 \(\frac{1}{5}\) = sin-1 x
[∵ sin-1 x + cos-1 x = \(\frac{\pi}{2}\)]
⇒ \(\frac{1}{5}\) = x
Hence, the value of x is \(\frac{1}{5}\).
Question 15.
If tan-1 \(\frac{x-1}{x-2}\) + tan-1 \(\frac{x+1}{x+2}=\frac{\pi}{4}\), then find the value of x.
Solution.
We have, tan-1 \(\frac{x-1}{x-2}\) + tan-1 \(\frac{x+1}{x+2}=\frac{\pi}{4}\)
⇒ 
![]()
Direction (16 – 18): Find the value of each expression.
Question 16.
sin-1 (sin \(\frac{2 \pi}{3}\))
Solution.
We have, sin-1 (sin \(\frac{2 \pi}{3}\))
We know that sin-1(sin x) = x , if x ∈ (- \(\frac{\pi}{2}\), \(\frac{\pi}{2}\)) which is the principal value branch of sin-1 x.
Here, \(\frac{2 \pi}{3}\) ∉ (- \(\frac{\pi}{2}\), \(\frac{\pi}{2}\)
Now, sin-1 (sin \(\frac{2 \pi}{3}\)) can be written as
sin-1 (sin \(\frac{2 \pi}{3}\)) = \(\sin ^{-1}\left[\sin \left(\pi-\frac{\pi}{3}\right)\right]=\sin ^{-1}\left(\sin \frac{\pi}{3}\right)\) where \(\frac{\pi}{3}\) ∈ (- \(\frac{\pi}{2}\), \(\frac{\pi}{2}\))
∴ sin-1 (sin \(\frac{2 \pi}{3}\)) = sin-1 (sin \(\frac{\pi}{3}\)) = \(\frac{\pi}{3}\)
Question 17.
tan-1 (tan \(\frac{3 \pi}{4}\))
Solution.
We have, tan-1 (tan \(\frac{3 \pi}{4}\))
We know that tan-1 (tan x) = x, if x ∈ (- \(\frac{\pi}{2}\), \(\frac{\pi}{2}\)), which is the principal value branch of tan-1 x.
Here, \(\frac{3 \pi}{4}\) ∉ (- \(\frac{\pi}{2}\), \(\frac{\pi}{2}\))
Now, tan-1 (tan \(\frac{3 \pi}{4}\)) can be written as
tan-1 (tan \(\frac{3 \pi}{4}\)) = tan-1 [tan(π – \(\frac{\pi}{4}\))]
= tan-1 [- tan \(\frac{\pi}{4}\)]
= tan-1 [tan (- \(\frac{\pi}{4}\))]
where – \(\frac{\pi}{4}\) ∈ (- \(\frac{\pi}{2}\), \(\frac{\pi}{2}\))
[∵ – tan θ = tan(- θ)]
∴ tan-1 (tan \(\frac{3 \pi}{4}\)) = tan-1 [tan (- \(\frac{\pi}{4}\))]
= – \(\frac{\pi}{4}\).
![]()
Question 18.
tan (sin-1 \(\frac{3}{5}\) + cot-1 \(\frac{3}{2}\))
Solution.
Let sin-1 \(\frac{3}{5}\) = x.
Then, sin x = \(\frac{3}{5}\)
⇒ cos x = \(\sqrt{1-\sin ^{2} x}\) = \(\frac{4}{5}\)
⇒ sec x = \(\frac{5}{4}\)
∴ tan x = \(\sqrt{\sec ^{2} x-1}=\sqrt{\frac{25}{16}-1}=\frac{3}{4}\)
∴ x = tan-1 \(\frac{3}{4}\)
∴ sin-1 \(\frac{3}{5}\) = tan-1 \(\frac{3}{4}\) ………..(i)
Now, cot-1 \(\frac{3}{2}\) = tan-1 \(\frac{2}{3}\)
[∵ tan-1 \(\frac{1}{x}\) = cot-1 x] ……………(ii)
Hence, tan (sin-1 \(\frac{3}{5}\) + cot-1 \(\frac{3}{2}\))
= tan (tan-1 \(\frac{3}{4}\) + tan-1 \(\frac{2}{3}\))
= \(\tan \left(\tan ^{-1} \frac{\frac{3}{4}+\frac{2}{3}}{1-\frac{3}{4} \cdot \frac{2}{3}}\right)\)
[∵ tan-1 x + tan-1 y = tan-1 \(\left(\frac{x+y}{1-x y}\right)\)]
= tan (tan-1 \(\frac{9+8}{12-6}\))
= tan (tan-1 \(\frac{17}{6}\))
= \(\frac{17}{6}\).
![]()
Question 19.
cos-1 (cos \(\frac{7 \pi}{6}\)) is equal to
(A) \(\frac{7 \pi}{6}\)
(B) \(\frac{5 \pi}{6}\)
(C) \(\frac{\pi}{3}\)
(D) \(\frac{\pi}{6}\)
Solution.
We know that cos-1 (cos x) = x if x ∈ [0, x], which is the principal value branch of cos-1 x.
Here, \(\frac{7 \pi}{6}\) ∉ x ∈ [0, π]
Now, cos-1 (cos \(\frac{7 \pi}{6}\)) can be written as
cos-1 (cos \(\frac{7 \pi}{6}\)) = cos-1 [cos(2π – \(\frac{5 \pi}{6}\))]
= cos-1 [cos \(\frac{5 \pi}{6}\)], where \(\frac{5 \pi}{6}\) ∈ [0, π]
[∵ cos(2π – x) = cos x]
∴ cos-1 (cos \(\frac{7 \pi}{6}\)) = cos-1 (cos \(\frac{5 \pi}{6}\))
= \(\frac{5 \pi}{6}\)
The correct option is (B).
![]()
Question 20.
sin[\(\frac{\pi}{3}\) – sin-1 (- \(\frac{1}{2}\))] is equal to
(A) \(\frac{1}{2}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{1}{4}\)
(D) 1
Solution.
Let sin-1 (- \(\frac{1}{2}\)) = x.
Then, sin x = – \(\frac{1}{2}\) = – sin \(\frac{\pi}{6}\) = sin(-\(\frac{\pi}{6}\))
We know that the range of the principal value of sin-1 x is (- \(\frac{\pi}{2}\), –\(\frac{\pi}{2}\))
∴ sin-1 (- \(\frac{1}{2}\)) = – \(\frac{\pi}{6}\)
Now, sin[\(\frac{\pi}{6}\) – sin-1 (- \(\frac{1}{2}\))] = sin \(\left[\frac{\pi}{3}-\left(-\frac{\pi}{6}\right)\right]\)
= sin \(\left(\frac{\pi}{3}+\frac{\pi}{6}\right)\)
= sin (\(\frac{3 \pi}{6}\))
= sin (\(\frac{\pi}{2}\)) = 1
The correct option is (D).
![]()
Question 21.
tan-1 (- √3) – cot-1 (- √3) is equal to
(A) π
(B) – \(\frac{\pi}{2}\)
(C) 0
(D) 2√3
Solution.
Let tan-1 √3 = x
⇒ tan x = √3 = tan \(\frac{\pi}{3}\)
∴ tan-1 √3 = \(\frac{\pi}{3}\)
Again, let cos-1(- √3) = x
⇒ cot x = – √3 = – cot \(\frac{\pi}{6}\)
= cot (π – \(\frac{\pi}{6}\))
= cot \(\frac{5 \pi}{6}\)
∴ cot-1 (- √3) = \(\frac{5 \pi}{6}\)
Now, tan-1 (- √3) – cot-1 (- √3) = \(\frac{\pi}{3}\) – \(\frac{5 \pi}{6}\)
= \(\frac{2 \pi-5 \pi}{6}=\frac{-3 \pi}{6}=-\frac{\pi}{2}\)
Hence, correct option is (B).
