PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 3 Matrices Ex 3.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 3 Matrices Ex 3.2

Question 1.
Let A = \(\left[\begin{array}{ll}
2 & 4 \\
3 & 2
\end{array}\right]\), B = \(\left[\begin{array}{cc}
1 & 3 \\
-2 & 5
\end{array}\right]\), C = \(\left[\begin{array}{cc}
-2 & 5 \\
3 & 4
\end{array}\right]\)
Find each of the following:
(i) A + B
(ii) A – B
(iii) 3A – C
(iv) AB
(v) BA
Solutions.
(i) A + B = \(\left[\begin{array}{ll}
2 & 4 \\
3 & 2
\end{array}\right]+\left[\begin{array}{cc}
1 & 3 \\
-2 & 5
\end{array}\right]\)

= \(\left[\begin{array}{cc}
2+1 & 4+3 \\
3-2 & 2+5
\end{array}\right]=\left[\begin{array}{ll}
3 & 7 \\
1 & 7
\end{array}\right]\)

(ii) A – B = \(\left[\begin{array}{ll}
2 & 4 \\
3 & 2
\end{array}\right]-\left[\begin{array}{cc}
1 & 3 \\
-2 & 5
\end{array}\right]\)

= \(\left[\begin{array}{cc}
2-1 & 4-3 \\
3-(-2) & 2-5
\end{array}\right]=\left[\begin{array}{cc}
1 & 1 \\
5 & -3
\end{array}\right]\)

(iii) 3A – C = 3\(\left[\begin{array}{ll}
2 & 4 \\
3 & 2
\end{array}\right]-\left[\begin{array}{cc}
-2 & 5 \\
3 & 4
\end{array}\right]\)

= \(\left[\begin{array}{ll}
3 \times 2 & 3 \times 4 \\
3 \times 3 & 3 \times 2
\end{array}\right]-\left[\begin{array}{cc}
-2 & 5 \\
3 & 4
\end{array}\right]\)

= \(\left[\begin{array}{cc}
6 & 12 \\
9 & 6
\end{array}\right]-\left[\begin{array}{cc}
-2 & 5 \\
3 & 4
\end{array}\right]\)

= \(\left[\begin{array}{cc}
6+2 & 12-5 \\
9-3 & 6-4
\end{array}\right]\)

= \(\left[\begin{array}{ll}
8 & 7 \\
6 & 2
\end{array}\right]\)

(iv) Matrix A has 2 columns. This number is equal to the number of rows in matrix B. Therefore, AB is defined as
AB = \(\left[\begin{array}{ll}
2 & 4 \\
3 & 2
\end{array}\right]\left[\begin{array}{cc}
1 & 3 \\
-2 & 5
\end{array}\right]\)

= \(\left[\begin{array}{ll}
2(1)+4(-2) & 2(3)+4(5) \\
3(1)+2(-2) & 3(3)+2(5)
\end{array}\right]\)

= \(\left[\begin{array}{ll}
2-8 & 6+20 \\
3-4 & 9+10
\end{array}\right]=\left[\begin{array}{ll}
-6 & 26 \\
-1 & 19
\end{array}\right]\)

(v) Matrix B has 2 columns. This number is equal to the number of rows in matrix A.
Therefore, BA is defined as
BA = \(\left[\begin{array}{cc}
1 & 3 \\
-2 & 5
\end{array}\right]\left[\begin{array}{ll}
2 & 4 \\
3 & 2
\end{array}\right]\)

= \(\left[\begin{array}{cc}
1(2)+3(3) & 1(4)+3(2) \\
-2(2)+5(3) & -2(4)+5(2)
\end{array}\right]\)

= \(\left[\begin{array}{cc}
2+9 & 4+6 \\
-4+15 & -8+10
\end{array}\right]=\left[\begin{array}{cc}
11 & 10 \\
11 & 2
\end{array}\right]\)

Question 2.
Compute the following:
(i) \(\left[\begin{array}{cc}
\boldsymbol{a} & \boldsymbol{b} \\
-\boldsymbol{b} & \boldsymbol{a}
\end{array}\right]+\left[\begin{array}{cc}
\boldsymbol{a} & \boldsymbol{b} \\
\boldsymbol{b} & \boldsymbol{a}
\end{array}\right]\)

(ii) \(\left[\begin{array}{cc}
a^{2}+b^{2} & b^{2}+c^{2} \\
a^{2}+c^{2} & a^{2}+b^{2}
\end{array}\right]+\left[\begin{array}{cc}
2 a b & 2 b c \\
-2 a c & -2 a b
\end{array}\right]\)

(iii) \(\left[\begin{array}{ccc}
-1 & 4 & -6 \\
8 & 5 & 16 \\
2 & 8 & 5
\end{array}\right]+\left[\begin{array}{ccc}
12 & 7 & 6 \\
8 & 0 & 5 \\
3 & 2 & 4
\end{array}\right]\)

(iv) \(\left[\begin{array}{cc}
\cos ^{2} x & \sin ^{2} x \\
\sin ^{2} x & \cos ^{2} x
\end{array}\right]+\left[\begin{array}{cc}
\sin ^{2} x & \cos ^{2} x \\
\cos ^{2} x & \sin ^{2} x
\end{array}\right]\)

Solution.
(i) \(\left[\begin{array}{cc}
\boldsymbol{a} & \boldsymbol{b} \\
-\boldsymbol{b} & \boldsymbol{a}
\end{array}\right]+\left[\begin{array}{cc}
\boldsymbol{a} & \boldsymbol{b} \\
\boldsymbol{b} & \boldsymbol{a}
\end{array}\right]\) = \(\left[\begin{array}{cc}
a+a & b+b \\
-b+b & a+a
\end{array}\right]=\left[\begin{array}{cc}
2 a & 2 b \\
0 & 2 a
\end{array}\right]\)

(ii) \(\left[\begin{array}{cc}
a^{2}+b^{2} & b^{2}+c^{2} \\
a^{2}+c^{2} & a^{2}+b^{2}
\end{array}\right]+\left[\begin{array}{cc}
2 a b & 2 b c \\
-2 a c & -2 a b
\end{array}\right]\) = \(\left[\begin{array}{ll}
a^{2}+b^{2}+2 a b & b^{2}+c^{2}+2 b c \\
a^{2}+c^{2}-2 a c & a^{2}+b^{2}-2 a b
\end{array}\right]\)

= \(\left[\begin{array}{ll}
(a+b)^{2} & (b+c)^{2} \\
(a-c)^{2} & (a-b)^{2}
\end{array}\right]\).

(iii) \(\left[\begin{array}{ccc}
-1 & 4 & -6 \\
8 & 5 & 16 \\
2 & 8 & 5
\end{array}\right]+\left[\begin{array}{ccc}
12 & 7 & 6 \\
8 & 0 & 5 \\
3 & 2 & 4
\end{array}\right]\) = \(\left[\begin{array}{ccc}
-1+12 & 4+7 & -6+6 \\
8+8 & 5+0 & 16+5 \\
2+3 & 8+2 & 5+4
\end{array}\right]\)

= \(\left[\begin{array}{ccc}
11 & 11 & 0 \\
16 & 5 & 21 \\
5 & 10 & 9
\end{array}\right]\)

(iv) \(\left[\begin{array}{cc}
\cos ^{2} x & \sin ^{2} x \\
\sin ^{2} x & \cos ^{2} x
\end{array}\right]+\left[\begin{array}{cc}
\sin ^{2} x & \cos ^{2} x \\
\cos ^{2} x & \sin ^{2} x
\end{array}\right]\) = \(\left[\begin{array}{ll}
\cos ^{2} x+\sin ^{2} x & \sin ^{2} x+\cos ^{2} x \\
\sin ^{2} x+\cos ^{2} x & \cos ^{2} x+\sin ^{2} x
\end{array}\right]\)

= \(\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\) [∵ sin² x + cos² x = 1].

Question 3.
Compute the indicated products:
(i) \(\left[\begin{array}{cc}
a & b \\
-b & a
\end{array}\right]\left[\begin{array}{cc}
a & -b \\
b & a
\end{array}\right]\)

(ii) \(\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]\left[\begin{array}{lll}
2 & 3 & 4
\end{array}\right]\)

(iii) \(\left[\begin{array}{cc}
1 & -2 \\
2 & 3
\end{array}\right]\left[\begin{array}{ccc}
1 & 2 & 3 \\
2 & 3 & 1
\end{array}\right]\)

(iv) \(\left[\begin{array}{lll}
2 & 3 & 4 \\
3 & 4 & 5 \\
4 & 5 & 6
\end{array}\right]\left[\begin{array}{ccc}
1 & -3 & 5 \\
0 & 2 & 4 \\
3 & 0 & 5
\end{array}\right]\)

(v) \(\left[\begin{array}{cc}
2 & 1 \\
3 & 2 \\
-1 & 1
\end{array}\right]\left[\begin{array}{ccc}
1 & 0 & 1 \\
-1 & 2 & 1
\end{array}\right]\)

(vi) \(\left[\begin{array}{ccc}
3 & -1 & 3 \\
-1 & 0 & 2
\end{array}\right]\left[\begin{array}{cc}
2 & -3 \\
1 & 0 \\
3 & 1
\end{array}\right]\)

Solution.
(i) \(\left[\begin{array}{cc}
a & b \\
-b & a
\end{array}\right]\left[\begin{array}{cc}
a & -b \\
b & a
\end{array}\right]\) = \(\left[\begin{array}{cc}
a(a)+b(b) & a(-b)+b(a) \\
-b(a)+a(b) & -b(-b)+a(a)
\end{array}\right]\)

=\(\left[\begin{array}{cc}
a^{2}+b^{2} & -a b+a b \\
-a b+a b & b^{2}+a^{2}
\end{array}\right]\)

= \(\left[\begin{array}{cc}
a^{2}+b^{2} & 0 \\
0 & a^{2}+b^{2}
\end{array}\right]\)

(ii) \(\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]\left[\begin{array}{lll}
2 & 3 & 4
\end{array}\right]\) = \(\left[\begin{array}{lll}
1(2) & 1(3) & 1(4) \\
2(2) & 2(3) & 2(4) \\
3(2) & 3(3) & 3(4)
\end{array}\right]=\left[\begin{array}{ccc}
2 & 3 & 4 \\
4 & 6 & 8 \\
6 & 9 & 12
\end{array}\right]\)

(iii) \(\left[\begin{array}{cc}
1 & -2 \\
2 & 3
\end{array}\right]\left[\begin{array}{ccc}
1 & 2 & 3 \\
2 & 3 & 1
\end{array}\right]\) = \(\left[\begin{array}{lll}
1(1)-2(2) & 1(2)-2(3) & 1(3)-2(1) \\
2(1)+3(2) & 2(2)+3(3) & 2(3)+3(1)
\end{array}\right]\)

= \(\left[\begin{array}{lll}
1-4 & 2-6 & 3-2 \\
2+6 & 4+9 & 6+3
\end{array}\right]=\left[\begin{array}{ccc}
-3 & -4 & 1 \\
8 & 13 & 9
\end{array}\right]\)

(iv) \(\left[\begin{array}{lll}
2 & 3 & 4 \\
3 & 4 & 5 \\
4 & 5 & 6
\end{array}\right]\left[\begin{array}{ccc}
1 & -3 & 5 \\
0 & 2 & 4 \\
3 & 0 & 5
\end{array}\right]\) =

(v) \(\left[\begin{array}{cc}
2 & 1 \\
3 & 2 \\
-1 & 1
\end{array}\right]\left[\begin{array}{ccc}
1 & 0 & 1 \\
-1 & 2 & 1
\end{array}\right]\) =

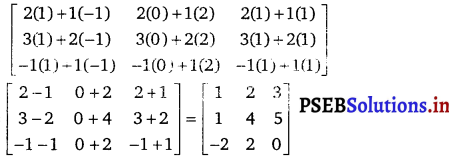
(vi) \(\left[\begin{array}{ccc}
3 & -1 & 3 \\
-1 & 0 & 2
\end{array}\right]\left[\begin{array}{cc}
2 & -3 \\
1 & 0 \\
3 & 1
\end{array}\right]\) =

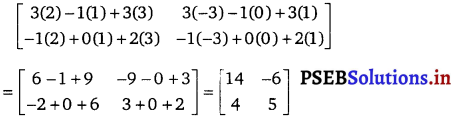
Question 4.
If A = \(\left[\begin{array}{ccc}
1 & 2 & -3 \\
5 & 0 & 2 \\
1 & -1 & 1
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
3 & -1 & 2 \\
4 & 2 & 5 \\
2 & 0 & 3
\end{array}\right]\) and C = \(\left[\begin{array}{ccc}
4 & 1 & 2 \\
0 & 3 & 2 \\
1 & -2 & 3
\end{array}\right]\) then compute (A + B) and (B – C). Also, verify that A + (B – C) = (A + B) – C.
Solution.

(A + B) – C = \(\left[\begin{array}{ccc}
4 & 1 & -1 \\
9 & 2 & 7 \\
3 & -1 & 4
\end{array}\right]-\left[\begin{array}{ccc}
4 & 1 & 2 \\
0 & 3 & 2 \\
1 & -2 & 3
\end{array}\right]\)

= \(\left[\begin{array}{ccc}
4-4 & 1-1 & -1-2 \\
9-0 & 2-3 & 7-2 \\
3-1 & -1-(-2) & 4-3
\end{array}\right]\)

= \(\left[\begin{array}{ccc}
0 & 0 & -3 \\
9 & -1 & 5 \\
2 & 1 & 1
\end{array}\right]\)
Hence, verified that A + (B – C) = (A + B) – C.

Question 5.
If A = \(\left[\begin{array}{ccc}
\frac{2}{3} & 1 & \frac{5}{3} \\
\frac{1}{3} & \frac{2}{3} & \frac{4}{3} \\
\frac{7}{3} & 2 & \frac{2}{3}
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
\frac{2}{5} & \frac{3}{5} & 1 \\
\frac{1}{5} & \frac{2}{5} & \frac{4}{5} \\
\frac{7}{5} & \frac{6}{5} & \frac{2}{5}
\end{array}\right]\)
Solution.

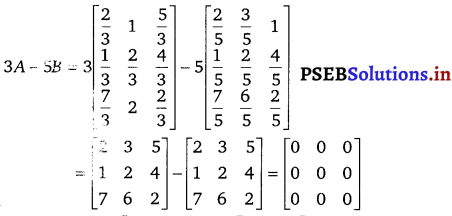
Question 6.
Simplify cos θ \(\left[\begin{array}{cc}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\) + sin θ \(\left[\begin{array}{cc}
\sin \theta & -\cos \theta \\
\cos \theta & \sin \theta
\end{array}\right]\).
Solution.

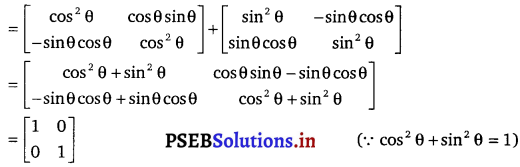
Question 7.
Find X and Y, if
(i) X + Y = \(\left[\begin{array}{ll}
7 & 0 \\
2 & 5
\end{array}\right]\) and X – Y = \(\left[\begin{array}{ll}
\mathbf{3} & \mathbf{0} \\
\mathbf{0} & \mathbf{3}
\end{array}\right]\)

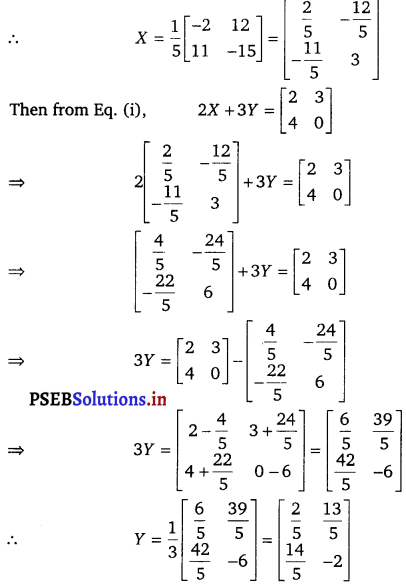
(ii) 2X + 3Y = \(\left[\begin{array}{ll}
2 & 3 \\
4 & 0
\end{array}\right]\) and 3X + 2Y = \(\left[\begin{array}{cc}
2 & -2 \\
-1 & 5
\end{array}\right]\).
Solution.

(i)

(ii)

Question 8.
Find X, if Y = \(\left[\begin{array}{ll}
3 & 2 \\
1 & 4
\end{array}\right]\) and 2X + Y = \(\left[\begin{array}{cc}
1 & 0 \\
-3 & 2
\end{array}\right]\).
Solution.

Question 9.
Find x and y, if 2\(\left[\begin{array}{ll}
1 & 3 \\
0 & x
\end{array}\right]+\left[\begin{array}{ll}
y & 0 \\
1 & 2
\end{array}\right]=\left[\begin{array}{ll}
5 & 6 \\
1 & 8
\end{array}\right]\)
Solution.

Question 10.
Solve the equation for x, y, z and t, if 2 \(\left[\begin{array}{cc}
x & z \\
y & t
\end{array}\right]+3\left[\begin{array}{cc}
1 & -1 \\
0 & 2
\end{array}\right]=3\left[\begin{array}{ll}
3 & 5 \\
4 & 6
\end{array}\right]\).
Solution.

On comparing the corresponding elements of these two matrices, we have
2x + 3 = 9
⇒ 2x = 6
⇒ x = 3

2y = 12
⇒ y = 6

2z – 3 = 15
⇒ 2z = 12
⇒ z = 6

2t + 6 = 18
⇒ 2t = 12
⇒ t = 6
Hence x = 3, y=6, z = 6 and t = 6.

Question 11.
If x\(\left[\begin{array}{l}
2 \\
3
\end{array}\right]\) + y\(\left[\begin{array}{r}
-1 \\
1
\end{array}\right]\) = \(\left[\begin{array}{c}
10 \\
5
\end{array}\right]\), then find the values of x and y.
Solution.
If, \(\left[\begin{array}{l}
2 \\
3
\end{array}\right]\) + y\(\left[\begin{array}{r}
-1 \\
1
\end{array}\right]\) = \(\left[\begin{array}{c}
10 \\
5
\end{array}\right]\)
⇒ \(\left[\begin{array}{l}
2 x \\
3 x
\end{array}\right]+\left[\begin{array}{c}
-y \\
y
\end{array}\right]=\left[\begin{array}{c}
10 \\
5
\end{array}\right]\)

⇒ \(\left[\begin{array}{l}
2 x-y \\
3 x+y
\end{array}\right]=\left[\begin{array}{c}
10 \\
5
\end{array}\right]\)

On comparing the corresponding elements of these two matrices, we get 2x – y = 10 and 3x + y = 5 ………….(ii)
On adding Eq. (i) and (ii), we get
5x = 15
⇒ x = 3
Now, 3x + y = 5
⇒ y = 5 – 3x
⇒ y = 5 – 9 = – 4
Hence, x = 3 and y = – 4.

Question 12.
Given 3 \(\left[\begin{array}{ll}
x & y \\
z & w
\end{array}\right]=\left[\begin{array}{cc}
x & 6 \\
-1 & 2 w
\end{array}\right]+\left[\begin{array}{cc}
4 & x+y \\
z+w & 3
\end{array}\right]\) find the values of x, y and z.
Solution.
Given, 3 \(\left[\begin{array}{ll}
x & y \\
z & w
\end{array}\right]=\left[\begin{array}{cc}
x & 6 \\
-1 & 2 w
\end{array}\right]+\left[\begin{array}{cc}
4 & x+y \\
z+w & 3
\end{array}\right]\)

⇒ \(\left[\begin{array}{ll}
3 x & 3 y \\
3 z & 3 w
\end{array}\right]=\left[\begin{array}{cc}
x+4 & 6+x+y \\
-1+z+w & 2 w+3
\end{array}\right]\)

On comparing the corresponding elements of these two matrices, we get
3x = x + 4
⇒ 2x = 4
⇒ x = 2
and 3y = 6 + x + y
⇒ 2y = 6 + x
⇒ 2y = 6+ 2
⇒ 2y = 8
⇒ y = 4
3w = 2w + 3
⇒ w = 3
3z = – 1 + z + w
⇒ 2z = – 1 + w = – 1 + 3 = 2
⇒ z = 1
Hence, x = 2, y = 4, z = 1, and w = 3.

Question 13.
If F(x) = \(\left[\begin{array}{ccc}
\cos x & -\sin x & 0 \\
\sin x & \cos x & 0 \\
0 & 0 & 1
\end{array}\right]\), show that F(x) F(y) = F(x + y).
Solution.

Question 14.
Show that
(i) \(\left[\begin{array}{cc}
5 & -1 \\
6 & 7
\end{array}\right]\left[\begin{array}{cc}
2 & 1 \\
3 & 4
\end{array}\right] \neq\left[\begin{array}{cc}
2 & 1 \\
3 & 4
\end{array}\right]\left[\begin{array}{cc}
5 & -1 \\
6 & 7
\end{array}\right]\)

(ii) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 1 & 0 \\
1 & 1 & 0
\end{array}\right]\left[\begin{array}{ccc}
-1 & 1 & 0 \\
0 & -1 & 1 \\
2 & 3 & 4
\end{array}\right] \neq\left[\begin{array}{ccc}
-1 & 1 & 0 \\
0 & -1 & 1 \\
2 & 3 & 4
\end{array}\right]\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 1 & 0 \\
1 & 1 & 0
\end{array}\right]\)
Solution.
(i)

(ii)

Question 15.
Find A² – 5A + 6I, if A = \(\left[\begin{array}{ccc}
\mathbf{2} & \mathbf{0} & \mathbf{1} \\
\mathbf{2} & \mathbf{1} & \mathbf{3} \\
\mathbf{1} & -\mathbf{1} & \mathbf{0}
\end{array}\right]\).
Solution.

Question 16.
If A = \(\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 2 & 1 \\
2 & 0 & 3
\end{array}\right]\), prove that A³ – 6A² + 7A + 2I = 0.
Solution.
A² = A . A
= \(\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 2 & 1 \\
2 & 0 & 3
\end{array}\right]\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 2 & 1 \\
2 & 0 & 3
\end{array}\right]\)

Question 17.
If A = \(\left[\begin{array}{ll}
3 & -2 \\
4 & -2
\end{array}\right]\) and I = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\), find k so that A² = kA – 2I
Solution.

⇒ \(\left[\begin{array}{ll}
1 & -2 \\
4 & -4
\end{array}\right]=\left[\begin{array}{cc}
3 k-2 & -2 k \\
4 k & -2 k-2
\end{array}\right]\)
On comparing the corresponding elements, we get
3k – 2 = 1
⇒ 3k = 3
⇒ k = 1
Thus, the value of k is 1.

Question 18.
If A = \(\left[\begin{array}{cc}
0 & -\tan \frac{\alpha}{2} \\
\tan \frac{\alpha}{2} & 0
\end{array}\right]\) and I is the identity matrix of order 2, show that I + A = (I – A) \(\left[\begin{array}{cc}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]\).
Solution.

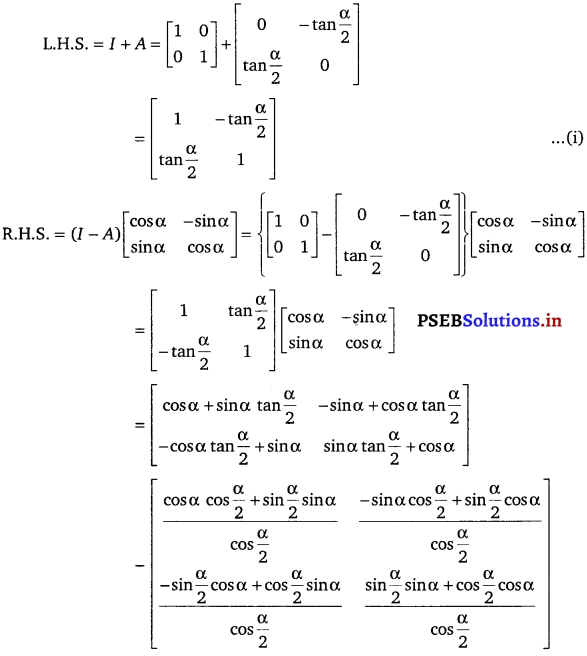
Thus, from Eqs. (i) and (ii), we get L.H.S = R.H.S.

Question 19.
A trust fund has ₹ 30000 that must be invested in two different types of bonds. The first bond pays 5 % interest per year, and the second bond pays 7 % interest per year. Using matrix multiplication, determine how to divide ₹ 30000 among the two types of bonds. If the trust fund must obtain an annual total interest of:
(a) ₹ 1800
(b) ₹ 2000
Solution.
(a) Let ₹ x be invested in the first bond. Then, the sum of money invested in the second bond will be ₹ (30000 – x).
It is given that the first bond pays 5% interest per year and the second bond pays 7% interest per year.
Therefore, in order to obtain an annual total interest of ₹ 1800, we have
⇒ 2x = 30000
⇒ x = 15000
Thus, in order to obtain an annual total interest of ₹ 1800, the trust fund should invest ₹ 15000 in the first bond and the remaining ?15000 in the second bond.

(b) Let ₹ x be invested in the first bond. Then, the sum of money invested in the second bond will be ₹ (30000 – x).
Therefore, in order to obtain an annual total interest of ₹ 2000, we have
[x (30000 – x)] \(\left[\begin{array}{c}
\frac{5}{100} \\
\frac{7}{100}
\end{array}\right]\) = [2000]

⇒ \(\frac{5 x}{100}+\frac{7(30000-x)}{100}\) = [2000]
⇒ 5x + 210000 – 7x = 200000
⇒ 210000 – 2x = 200000
⇒ 2x = 210000 – 200000
⇒ 2x = 10000
⇒ x = 5000
Thus, in order to obtain an annual total interest of ?2000, the trust fund should invest ₹ 5000 in the first bond and the remaining ₹ 25000 in the second bond.

Question 20.
The bookshop of a particular school has 10 dozen Chemistry books, 8 dozen Physics books and 10 dozen Economics books. Their selling prices are ₹ 80, ₹ 60, and ₹ 40 each respectively. Find the total amount the bookshop will receive from selling all the books using matrix algebra.
Solution.
The bookshop has 10 dozen Chemistry books, 8 dozen Physics book and 10 dozen Economics books.
The selling prices of a Chemistry book, a Physics book and an Economics book are respectively given as ₹ 80, ₹ 60 and ₹ 40.
The total amount of money that will be received from the sale of all,these books can be represented in the form of a matrix as
12 [10 8 10] \(\left[\begin{array}{l}
80 \\
60 \\
40
\end{array}\right]\)
= 12[10 × 80 + 8 × 60 + 10 × 40]
= 12 [800 + 480 + 400]
= 12(1680) = 20160
Thus, the bookshop will receive ₹ 20160 from the sale of all these books.

Direction (21 – 22)
Assume X, Y, Z, W and P are matrices of order 2 × n, 3 × k, 2 × p, n × 3, and p × k, respectively. Choose the correct answer in Q. 21 and Q. 22.

Question 21.
The restrictions on n, k and p so that PY + WY will be defined, are
(A) k – 3, p = n
(B) k is arbitrary, p = 2
(C) p is arbitrary, k – 3
(D) k = 2, p = 3
Solution.
Matrices P and Y are of the orders p × k and 3 × k, respectively.
Therefore, matrix PY will be defined if k – 3. Consequently, PY will be of the order p × k.
Matrices W and Y are of the orders n × 3 and 3 × k, respectively.
Since, the number of columns in W is equal to the number of rows in Y, matrix WY is well-defined and is of the order n × k.
Matrices PY and WY can be added only when their orders are the same. However, PY is of the order p × k and WY is of the order n × k. Therefore, we must have p = n.
Thus, k = 3 and p = n are the restrictions on n, k and p so that PY + WY will be defined.
Hence, the correct answer is (A).

Question 22.
If n = p, then the order of the matrix IX – 5Z is
(A) p × 2
(B) 2 × n
(C) C n × 3
(D) p × n
Solution.
Matrix X is of the order 2 × n.
Therefore, matrix 7X is also of the same order.
Matrix Z is of the order 2 × p,i.e., 2 × n [∵ n = p]
Therefore, matrix 5Z is also of the same order.
Now, both the matrices 7X and 5Z are of the order 2 × n.
Thus, matrix 7X – 5Z is well-defined and is of the order 2 × n.
Hence, the correct answer is (B).