PSEB 12th Class Maths Solutions Chapter 4 Determinants Ex 4.5

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 4 Determinants Ex 4.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 4 Determinants Ex 4.5

Direction (1 – 2): Find adjoint of each of the matrices.

Question 1.
\(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\)
We have,
A₁₁ = 4, A₁₂ = – 3, A₂₁ = – 2, A₂₂ = 1
∴ adj(A) = \(\left[\begin{array}{ll}
A_{11} & A_{12} \\
A_{21} & A_{22}
\end{array}\right]^{T}=\left[\begin{array}{rr}
4 & -3 \\
-2 & 1
\end{array}\right]^{T}=\left[\begin{array}{cc}
4 & -2 \\
-3 & 1
\end{array}\right]\).

Question 2.
\(\left[\begin{array}{ccc}
1 & -1 & 2 \\
2 & 3 & 5 \\
-2 & 0 & 1
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
2 & 3 & 5 \\
-2 & 0 & 1
\end{array}\right]\)
We have, A₁₁ = \(\left|\begin{array}{ll}
3 & 5 \\
0 & 1
\end{array}\right|\) = 3 – 0 = 3

A₁₂ = \(-\left|\begin{array}{cc}
2 & 5 \\
-2 & 1
\end{array}\right|\) = -(2 + 10) = – 12

A₁₃ = \(\left|\begin{array}{cc}
2 & 3 \\
-2 & 0
\end{array}\right|\) = 0 + 6 = 6

A₂₁ = \(-\left|\begin{array}{cc}
-1 & 2 \\
0 & 1
\end{array}\right|\) = -(- 1 – 0) = 1

A₂₂ = \(\left|\begin{array}{cc}
1 & 2 \\
-2 & 1
\end{array}\right|\) = 1 + 4 = 5

A₂₃ = \(-\left|\begin{array}{cc}
1 & -1 \\
-2 & 0
\end{array}\right|\) = – (0 – 2) = 2

A₃₁ = \(\left|\begin{array}{cc}
-1 & 2 \\
3 & 5
\end{array}\right|\) = – 5 – 6 = – 11

A₃₂ = \(-\left|\begin{array}{ll}
1 & 2 \\
2 & 5
\end{array}\right|\) = – (5 – 4) = – 1

A₃₃ = \(\left|\begin{array}{cc}
1 & -1 \\
2 & 3
\end{array}\right|\) = 3 + 2 = 5.

Direction (3 – 4): Verify A(adj A) = (adj A)A = |A| I.

Question 3.
\(\left[\begin{array}{cc}
2 & 3 \\
-4 & -6
\end{array}\right]\)
Sol.
Let A = \(\left[\begin{array}{cc}
2 & 3 \\
-4 & -6
\end{array}\right]\), |A| = \(\left|\begin{array}{rr}
2 & 3 \\
-4 & -6
\end{array}\right|\)
= – 12 – (- 12) = – 12 + 12 = 0
|A| = – 12 – (- 12) = – 12 + 12 = 0
∴ |A| = \(0\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]=\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\)
Now, A₁₁ = – 6, A₁₂ = 4, A₂₁ = – 3, A₂₂ = 2
∴ adj (A) = \(\left[\begin{array}{cc}
-6 & -3 \\
4 & 2
\end{array}\right]\)

Now, A (adj A) = \(\left[\begin{array}{cc}
2 & 3 \\
-4 & -6
\end{array}\right]\left[\begin{array}{cc}
-6 & -3 \\
4 & 2
\end{array}\right]\)

= \(\left[\begin{array}{cc}
-12+12 & -6+6 \\
24-24 & 12-12
\end{array}\right]=\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\)

Also, (adj A) A = \(\left[\begin{array}{cc}
-6 & -3 \\
4 & 2
\end{array}\right]\left[\begin{array}{cc}
2 & 3 \\
-4 & -6
\end{array}\right]\)

= \(\left[\begin{array}{cc}
-12+12 & -18+18 \\
8-8 & 12-12
\end{array}\right]=\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\)

Hence, A (adj A) = (adj A) A = |A| I.

Question 4.
\(\left[\begin{array}{ccc}
1 & -1 & 2 \\
3 & 0 & -2 \\
1 & 0 & 3
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
3 & 0 & -2 \\
1 & 0 & 3
\end{array}\right]\)
Now, |A| = 1 (0 – 0) + 1 (9 + 2) + 2 (0 – 0) = 11

∴ |A| I = \(11\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]=\left[\begin{array}{ccc}
11 & 0 & 0 \\
0 & 11 & 0 \\
0 & 0 & 11
\end{array}\right]\)

Now, A₁₁ = 0, A₁₂ = – (9 + 2) = – 11, A₁₃ = 0
A₂₁ = – (- 3 – 0) = 3, A₂₂ = 3 – 2 = 1, A₂₃ = – (0 + 1) = – 1
A₃₁ = 2 – 0 = 2, A₃₂ = – (- 2 – 6) = 8, A₃₃ = 0 + 3 = 3

Direction (5 – 11): Find the inverse of the matrices (if it exists).

Question 5.
\(\left[\begin{array}{cc}
2 & -2 \\
4 & 3
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{cc}
2 & -2 \\
4 & 3
\end{array}\right]\)

We have, |A| = \(\left|\begin{array}{cc}
2 & -2 \\
4 & 3
\end{array}\right|\) = 6 – (- 8) = 14
Cofactors of A are
A₁₁ = 3,
A₁₂ = – 4,
A₂₁ = 2,
A₂₂ = 2

(Note: If determinant of any matrix is zero, then its inverse does not exist.)

Question 6.
\(\left[\begin{array}{cc}
-1 & 5 \\
-3 & 2
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{cc}
-1 & 5 \\
-3 & 2
\end{array}\right]\)
We have, |A| = \(\) = – 2 + 15 = 13
Now, Cofactors of A are
A = 2,
A = 3,
A = – 5,
A = – 1
adj (A) = \(\left[\begin{array}{rr}
2 & -5 \\
3 & -1
\end{array}\right]\)

A^-1 = \(\frac{1}{|A|}\) (adj A)
= \(\frac{1}{13}\left[\begin{array}{cc}
2 & -5 \\
3 & -1
\end{array}\right]=\left[\begin{array}{cc}
\frac{2}{13} & -\frac{5}{13} \\
\frac{3}{13} & -\frac{1}{13}
\end{array}\right]\)

Question 7.
\(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 2 & 4 \\
0 & 0 & 5
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 2 & 4 \\
0 & 0 & 5
\end{array}\right]\)

We have, |A| = 1 (10 – 0) – 2 (0 – 0) + 3 (0 – 0)= 10
Cofactors of A are
A₁₁ = 10 – 0 =10,
A₁₂ = – (0 – 0) = 0,
A₁₃ = 0 – 0 = 0
A₂₁ = – (10 – 0) = – 10,
A₂₂ = 5 – 0 = 5,
A₂₃ = – (0 – 0) = 0
A₃₁ = 8 – 6 = 2,
A₃₂ = – (4 – 0) = – 4,
A₃₃ = 2 – 0 = 2

∴ adj (A) = \(\left[\begin{array}{ccc}
10 & -10 & 2 \\
0 & 5 & -4 \\
0 & 0 & 2
\end{array}\right]\)

A^-1 = \(\frac{1}{|A|}\) (adj A)

= \(\frac{1}{10}\left[\begin{array}{ccc}
10 & -10 & 2 \\
0 & 5 & -4 \\
0 & 0 & 2
\end{array}\right]=\left[\begin{array}{ccc}
1 & -1 & \frac{1}{5} \\
0 & \frac{1}{2} & -\frac{2}{5} \\
& 0 & \frac{1}{5}
\end{array}\right]\)

Question 8.
\(\left[\begin{array}{ccc}
1 & 0 & 0 \\
3 & 3 & 0 \\
5 & 2 & -1
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
3 & 3 & 0 \\
5 & 2 & -1
\end{array}\right]\)
We have, |A| = 1 (- 3 – 0) – 0 + 0 = – 3
Cofactors of A are
A₁₁ = – 3 – 0 = – 3
A₁₂ = – (- 3 – 0) = 3
A₁₃ = 6 – 15 = – 9
A₂₁ = – (0 – 0) = 0
A₂₂ = – 1 – 0 = – 1
A₂₃ = – (2 – 0) = – 2
A₃₁ = 0 – 0 = 0
A₃₂ = – (0 – 0) = 0
A₃₃ = 3 – 0 = 3

∴ adj(A) = \(\left[\begin{array}{ccc}
-3 & 0 & 0 \\
3 & -1 & 0 \\
-9 & -2 & 3
\end{array}\right]\)

∴ A^-1 = \(\frac{1}{|A|}\) (adj A)

= \(-\frac{1}{3}\left[\begin{array}{ccc}
-3 & 0 & 0 \\
3 & -1 & 0 \\
-9 & -2 & 3
\end{array}\right]=\left[\begin{array}{ccc}
1 & 0 & 0 \\
-1 & \frac{1}{3} & 0 \\
& \frac{2}{3} & -1
\end{array}\right]\)

Question 9.
\(\left[\begin{array}{ccc}
2 & 1 & 3 \\
4 & -1 & 0 \\
-7 & 2 & 1
\end{array}\right]\)
Solution.
\(\left[\begin{array}{ccc}
2 & 1 & 3 \\
4 & -1 & 0 \\
-7 & 2 & 1
\end{array}\right]\)

We have, |A| = 2 (- 1 – 0) – 1 (4 – 0) + 3 (8 – 7)
= 2 (- 1) – 1 (4) + 3(1)
= – 2 – 4 + 3 = – 3
Cofactors of A are
A₁₁ = – 1 – 0 = – 1,
A₁₂ = – (4 – 0) = – 4,
A₁₃ = 8 – 7 = 1
A₂₁ = – (1 – 6) = 5,
A₂₂ = 2 + 21 = 23,
A₂₃ = – (4 + 7) = – 11
A₃₁ = 0 + 3 = 3,
A₃₂ = – (0 – 12) = 12,
A₃₃ = – 2 – 4 = – 6

∴ adj (A) = \(\left[\begin{array}{ccc}
-1 & 5 & 3 \\
-4 & 23 & 12 \\
1 & -11 & -6
\end{array}\right]\)

∴ A^-1 = \(\frac{1}{|A|}\) (adj A)
= \(-\frac{1}{3}\left[\begin{array}{ccc}
-1 & 5 & 3 \\
-4 & 23 & 12 \\
1 & -11 & -6
\end{array}\right]=\left[\begin{array}{ccc}
\frac{1}{3} & -\frac{5}{3} & -1 \\
\frac{4}{3} & -\frac{23}{3} & -4 \\
-\frac{1}{3} & \frac{11}{3} & 2
\end{array}\right]\)

Question 10.
\(\left[\begin{array}{ccc}
1 & -1 & 2 \\
0 & 2 & -3 \\
3 & -2 & 4
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
0 & 2 & -3 \\
3 & -2 & 4
\end{array}\right]\)

We have, |A| = 1(8 – 6) – 0 + 3 (3 – 4) = 2 – 3 = – 1
Cofactors of A are
A₁₁ = 8 – 6 = 2
A₁₂ = – (0 + 9) = – 9
A₁₃ = 0 – 6 = – 6
A₂₁ = – (- 4 + 4) = 0,
A₂₂ =4 – 6 = – 2,
A₂₃ = – (- 2 + 3) = – 1
A₃₁ = 3 – 4 = – 1,
A₃₂ = – (- 3 – 0)= 3,
A₃₃ = 2 – 0 = 2
∴ adj (A) = \(\left[\begin{array}{ccc}
2 & 0 & -1 \\
-9 & -2 & 3 \\
-6 & -1 & 2
\end{array}\right]\)
∴ A^-1 = \(\frac{1}{|A|}\) adj (A)
= \(\frac{1}{-1}\left[\begin{array}{ccc}
2 & 0 & -1 \\
-9 & -2 & 3 \\
-6 & -1 & 2
\end{array}\right]=\left[\begin{array}{ccc}
-2 & 0 & 1 \\
9 & 2 & -3 \\
6 & 1 & -2
\end{array}\right]\)

Question 11.
\(\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & \cos \alpha & \sin \alpha \\
0 & \sin \alpha & -\cos \alpha
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & \cos \alpha & \sin \alpha \\
0 & \sin \alpha & -\cos \alpha
\end{array}\right]\)

We have, |A| = 1(- cos² α – sin² α)
= – (cos² α + sin² α) = – 1
Cofactors of A are
A₁₁ = – cos² α – sin² α = – 1,
A₁₂ = 0,
A₁₃ = 0,
A₂₁ = 0,
A₂₂ = – cos α,
A₂₃ = – sin α
A₃₁ = 0,
A₃₂ = – sin α,
A₃₃ = cos α

∴ adj (A) = \(\left[\begin{array}{ccc}
-1 & 0 & 0 \\
0 & -\cos \alpha & -\sin \alpha \\
0 & -\sin \alpha & \cos \alpha
\end{array}\right]\)

∴ A^-1 = \(\frac{1}{|A|}\) (adj A)
= \(=\frac{1}{-1}\left[\begin{array}{ccc}
-1 & 0 & 0 \\
0 & -\cos \alpha & -\sin \alpha \\
0 & -\sin \alpha & \cos \alpha
\end{array}\right]=\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & \cos \alpha & \sin \alpha \\
0 & \sin \alpha & -\cos \alpha
\end{array}\right]\)

Question 12.
Let A = \(\left[\begin{array}{ll}
3 & 7 \\
2 & 5
\end{array}\right]\) and B = \(\left[\begin{array}{ll}
6 & 8 \\
7 & 9
\end{array}\right]\). verify that (AB)^-1 = B^-1 A^-1
Solution.
Let A = \(\left[\begin{array}{ll}
3 & 7 \\
2 & 5
\end{array}\right]\)
We have, |A| = 15 – 14 = 1
Cofactors of A are
A₁₁ = 5,
A₁₂ = – 2,
A₂₁ = – 7,
A₂₂ = 3
∴ adj (A) = \(\left[\begin{array}{cc}
5 & -7 \\
-2 & 3
\end{array}\right]\)

∴ A = \(\frac{1}{|A|}\) (adj A)
= \(\frac{1}{1}\left[\begin{array}{cc}
5 & -7 \\
-2 & 3
\end{array}\right]\)

Now, let B = \(\left[\begin{array}{ll}
6 & 8 \\
7 & 9
\end{array}\right]\)
We have, |B| = 54 – 56 = – 2
Cofactors of B are
B₁₁ = 9,
B₁₂ = – 7,
B₂₁ = – 8,
B₂₂ = 6

∴ adj (B) = \(\left[\begin{array}{cc}
9 & -8 \\
-7 & 6
\end{array}\right]\)

∴ B^-1 = \(\frac{1}{|B|}\) adj (B)
\(-\frac{1}{2}\left[\begin{array}{cc}
9 & -8 \\
-7 & 6
\end{array}\right]=\left[\begin{array}{cc}
-\frac{9}{2} & 4 \\
\frac{7}{2} & -3
\end{array}\right]\)

Now, B^-1A^-1 = \(\left[\begin{array}{cc}
-\frac{9}{2} & 4 \\
\frac{7}{2} & -3
\end{array}\right]\left[\begin{array}{cc}
5 & -7 \\
-2 & 3
\end{array}\right]\)

From Eqs. (i) and (ii), we have
(AB)^-1 = B^-1 A^-1
Hence, the given result is proved.

Question 13.
If A = \(\left[\begin{array}{cc}
3 & 1 \\
-1 & 2
\end{array}\right]\), show that A² – 5A + 7 I = 0. Hence find A^-1.
Solution.

∵ |A| = \(\left|\begin{array}{rr}
3 & 1 \\
-1 & 2
\end{array}\right|\)
= 6 + 1 = 7 ≠ 0
∴ A^-1 exists.
Hence, A² – 5A + 7I = 0.
∴ A . A – 5A = – 7I
⇒ A . A(A^-1) – 5AA^-1 = – 7IA^-1 [multiplying by A^-1 on both sides]
⇒ A(AA^-1) – 5I = – 7A^-1
⇒ AI – 5I = – 7A^-1
⇒ A^-1 = \(\frac{1}{7}\) (A – 5I)
= \(\frac{1}{7}\left(\left[\begin{array}{cc}
5 & 0 \\
0 & 5
\end{array}\right]-\left[\begin{array}{cc}
3 & 1 \\
-1 & 2
\end{array}\right]\right)=\frac{1}{7}\left[\begin{array}{cc}
2 & -1 \\
1 & 3
\end{array}\right]\)

∴ A^-1 = \(\frac{1}{7}\left[\begin{array}{cc}
2 & -1 \\
1 & 3
\end{array}\right]\)

Question 14.
For a matrix A \(\left[\begin{array}{ll}
3 & 2 \\
1 & 1
\end{array}\right]\), find the numbers a and b such that A² + aA + bI = 0.
Solution.

If two matrices are equal, then their corresponding elements are equal.
11 + 3a + b = 0 ………….(i)
8 + 2a = 0 …….(ii)
4 + a = 0 ………..(iii)
and 3 + a + b = 0 …………..(iv)
Solving Eqs. (iii) and (iv), we get
4 + a
⇒ a = – 4
and 3 + a + b = 0
⇒ 3 – 4 + b = 0
⇒ b = 1
Thus, a = – 4 and b = 1.

Question 15.
For the matrix A = \(\left[\begin{array}{ccc}
\mathbf{1} & \mathbf{1} & \mathbf{1} \\
\mathbf{1} & \mathbf{2} & -\mathbf{3} \\
\mathbf{2} & -\mathbf{1} & \mathbf{3}
\end{array}\right]\), show that A³ – 6A² + 5A + 11I = 0. Hence, find A^-1.
Solution.
Given, A = \(\left[\begin{array}{ccc}
\mathbf{1} & \mathbf{1} & \mathbf{1} \\
\mathbf{1} & \mathbf{2} & -\mathbf{3} \\
\mathbf{2} & -\mathbf{1} & \mathbf{3}
\end{array}\right]\)

Now, A³ – 6A² + 5A + 11I = 0
⇒ (AAA)A^-1 – 6(AA)A^-1 + 5AA^-1 +11IA^-1 = 0
[Pre-multiplying by A^-1 as |A| ≠ 0]
⇒ AA(AA^-1) – 6A(AA^-1) + 5(AA^-1) = -11(IA^-1)
⇒ A² – 6A + 5I = – 11A^-1
⇒ A^-1 = – \(\frac{1}{11}\) (A² – 6A + 5I) …………(i)
Now, A² – 6A + 5I

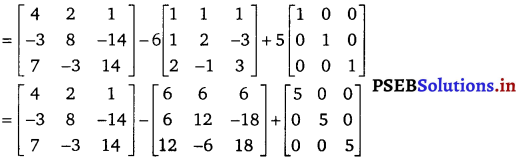
= \(\left[\begin{array}{ccc}
9 & 2 & 1 \\
-3 & 13 & -14 \\
7 & -3 & 19
\end{array}\right]-\left[\begin{array}{ccc}
6 & 6 & 6 \\
6 & 12 & -18 \\
12 & -6 & 18
\end{array}\right]=\left[\begin{array}{ccc}
3 & -4 & -5 \\
-9 & 1 & 4 \\
-5 & 3 & 1
\end{array}\right]\)

From eq. (i), we have

A^-1 = \(-\frac{1}{11}\left[\begin{array}{ccc}
3 & -4 & -5 \\
-9 & 1 & 4 \\
-5 & 3 & 1
\end{array}\right]=\frac{1}{11}\left[\begin{array}{ccc}
-3 & 4 & 5 \\
9 & -1 & -4 \\
5 & -3 & -1
\end{array}\right]\)

Question 16.
If A = \(\left[\begin{array}{ccc}
2 & -1 & 1 \\
-1 & 2 & -1 \\
1 & -1 & 2
\end{array}\right]\), then verify that A³ – 6A² + 9A – 4I = 0 and hence, find A^-1.
Solution.

∴ A³ – 6A² + 9A – 4I = 0
⇒ (AAA) A^-1 – 6(AA)A^-1 + 9 AA^-1 – 4 IA^-1 = 0
[pre-multiplying by A^-1 as |A| ≠ 0]
⇒ AA(AA^-1) – 6 A(AA^-1) + 9 (AA^-1) = 4(IA^-1)
⇒ AAI – 6AI + 9 I = 4A^-1
⇒ A² – 6A + 9I = 4 A^-1
⇒ A^-1 = \(\frac{1}{4}\) (A² – 6A +9I)
Now, A² – 6A +9I
= \(\left[\begin{array}{ccc}
6 & -5 & 5 \\
-5 & 6 & -5 \\
5 & -5 & 6
\end{array}\right]-6\left[\begin{array}{ccc}
2 & -1 & 1 \\
-1 & 2 & -1 \\
1 & -1 & 2
\end{array}\right]+9\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)

= \(\left[\begin{array}{ccc}
6 & -5 & 5 \\
-5 & 6 & -5 \\
5 & -5 & 6
\end{array}\right]-\left[\begin{array}{ccc}
12 & -6 & 6 \\
-6 & 12 & -6 \\
6 & -6 & 12
\end{array}\right]+\left[\begin{array}{ccc}
9 & 0 & 0 \\
0 & 9 & 0 \\
0 & 0 & 9
\end{array}\right]=\left[\begin{array}{ccc}
3 & 1 & -1 \\
1 & 3 & 1 \\
-1 & 1 & 3
\end{array}\right]\)

From Eq. (i) we have A^-1 = \(\frac{1}{4}\) \(\left[\begin{array}{ccc}
3 & 1 & -1 \\
1 & 3 & 1 \\
-1 & 1 & 3
\end{array}\right]\)

Question 17.
Let A be a non-singular square matrix of order 3 x 3. Then,
Ia4jAIIs equal to
(A) A
(B) A²
(C) A³
(D) 3|A|
Solution.
We know that,

Hence, the correct answer is (B).

Question 18.
If A is an invertible matrix of order 2, then det (A’) is equal to
(A) det |A|
(B) \(\frac{1}{\ det (A)}\)
(C) 1
(D) 0
Solution.
Since, A is an invertible matrix. So, A^-1 exists and A^-1 = \(\frac{1}{|A|}\) adj (A).

Hence, the correct answer is (B).