PSEB 12th Class Maths Solutions Chapter 4 Determinants Miscellaneous Exercise

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 4 Determinants Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 4 Determinants Miscellaneous Exercise

Question 1.
Prove that the determinant \(\left|\begin{array}{ccc}
x & \sin \theta & \cos \theta \\
-\sin \theta & -x & 1 \\
\cos \theta & 1 & x
\end{array}\right|\) is independent of θ.
Solution.
Let ∆ = \(\left|\begin{array}{ccc}
x & \sin \theta & \cos \theta \\
-\sin \theta & -x & 1 \\
\cos \theta & 1 & x
\end{array}\right|\)
On expanding to corresponding first row, we get
= x(- x² – 1) – sin θ (- x sin θ – cos θ) + cos θ(- sin θ + x cos θ)
= – x³ – x + x sin² θ + sinθ cos θ – sin θ cos θ + x cos² θ
= – x³ – x + x(sin² θ + cos² θ) [∵ sin² θ +cos² θ = 1]
= – x³ – x + x = – x³
Hence, ∆ is independent of θ.

Question 2.
Without expanding the determinant, prove that
\(\left|\begin{array}{lll}
a & a^{2} & b c \\
b & b^{2} & c a \\
c & c^{2} & a b
\end{array}\right|=\left|\begin{array}{ccc}
1 & a^{2} & a^{3} \\
1 & b^{2} & b^{3} \\
1 & c^{2} & c^{3}
\end{array}\right|\)
Solution.

Question 3.
Evaluate \(\left|\begin{array}{ccc}
\cos \alpha \cos \beta & \cos \alpha \sin \beta & -\sin \alpha \\
-\sin \beta & \cos \beta & 0 \\
\sin \alpha \cos \beta & \sin \alpha \sin \beta & \cos \alpha
\end{array}\right|\)
Solution.
Let ∆ = \(\left|\begin{array}{ccc}
\cos \alpha \cos \beta & \cos \alpha \sin \beta & -\sin \alpha \\
-\sin \beta & \cos \beta & 0 \\
\sin \alpha \cos \beta & \sin \alpha \sin \beta & \cos \alpha
\end{array}\right|\)

By expanding along C₃ we have
∆ = – sin α (- sin α sin² β – cos2 β sin α) + cos α (cos α cos2 β + cos α sin2 β)
= sin² α (sin² β + cos² β) + cos² α (cos² β + sin² β)
= sin² α (1) + cos² α (1)
= 1 [∵ sin² θ + cos² θ = 1].

Question 4.
If a, b and c are real numbers, and ∆ = \(\left|\begin{array}{lll}
b+c & c+a & a+b \\
c+a & a+b & b+c \\
a+b & b+c & c+a
\end{array}\right|\) = 0.
Show that, either a + b + c = 0 or a = b= c.
Solution.
Given ∆ = \(\left|\begin{array}{lll}
b+c & c+a & a+b \\
c+a & a+b & b+c \\
a+b & b+c & c+a
\end{array}\right|\)

By expanding along R1, we have
∆ = 2(a + b + c)(1) [(b – c) (c – b) – (b – a) (c – a)]
= 2 (a + b + c) [- b² – c² + 2bc – bc + ba + ac – a²]
= 2(a + b + c) [ab + bc + ca – a² – b² – c²]
It is given that ∆ = 0.
(a + b + c) [ab + bc + ca – a² – b² – c²] = 0
⇒ Either a + b + c = 0, or ab + bc + ca – a² – b² – c² = 0
Now, ab + bc + ca – a² – b² – c² = 0
⇒ – 2ab – 2bc – 2ca + 2a² + 2b² + 2c² = 0
⇒ (a – b)² + (b – c)² + (c – a)² = 0
⇒ (a – b)² = (b – c)² = (c – a)² = 0
[Since (a – b)², (b – c)² and (c – a)² are non – negative]
⇒ (a – b) = (b – c) = (c – a)
⇒ a = b = c
Hence, if ∆ = 0, then either a + b + c = 0 or a = b = c.

Question 5.
Solve the equation \(\left|\begin{array}{ccc}
x+a & x & x \\
x & x+a & x \\
x & x & x+a
\end{array}\right|\) = 0, a ≠ 0
Solution.

(3x + a) \(\left|\begin{array}{lll}
1 & 0 & 0 \\
x & a & 0 \\
x & 0 & a
\end{array}\right|\) = 0

(App1ying C₂ → C₂ – C₁ and C₃ → C₃ – C₁)
By expanding along R₁ we have
(3x + a) [1 × a²] = 0
⇒ a² (3x + a) = 0
But a ≠ 0
Therefore, 3x + a = 0
x = – \(\frac{a}{3}\)

Question 6.
Prove that \(\left|\begin{array}{ccc}
a^{2} & b c & a c+c^{2} \\
a^{2}+a b & b^{2} & a c \\
a b & b^{2}+b c & c^{2}
\end{array}\right|\) = 4a²b²c²
Solution.

By expanding along R₃, we have
∆ = 2ab²c [a(c – a) + a(a +c)]
= 2ab²c[ac – a² + a² + ac]
= 2ab²c(2ac)
= 4a²b²c²
Hence, the given result is proved.

Question 7.
If A^-1 = \(\left[\begin{array}{crr}
3 & -1 & 1 \\
-15 & 6 & -5 \\
5 & -2 & 2
\end{array}\right]\) and B = \(\left[\begin{array}{rrr}
1 & 2 & -2 \\
-1 & 3 & 0 \\
0 & -2 & 1
\end{array}\right]\), find (AB)^-1.
Solution.
We kncw that (AB)^-1 = B^-1A^-1 and A^-1 is known therefore, we proceed to find B^-1
Here, |B| = \(\left|\begin{array}{rrr}
1 & 2 & -2 \\
-1 & 3 & 0 \\
0 & -2 & 1
\end{array}\right|\)
= 1 (3 – 0) – 2(- 1 – 0) – 2 (2 – 0)
= 3 + 2 – 4 = 1 ≠ 0
Thus, B is non-singular.
Therefore, its inverse exists.
Cofactors of B are
B₁₁ = (3 – 0) = 3,
B₁₂ = – (- 1 – 0) = 1,
B₁₃ = (2 – 0) = 2,
B₂₁ = – (2 – 4) = – 2,
B₂₂ = 1 – 0 = 1,
B₂₃ = – (- 2 – 0) = 2,
B₃₁ = (0 + 6) = 6,
B₃₂ = – (0 – 2) =2,
B₃₃ = 3 + 2 = 5

Question 8.
Let A = \(\left[\begin{array}{rrr}
1 & -2 & 1 \\
-2 & 3 & 1 \\
1 & 1 & 5
\end{array}\right]\). verify that
(i) [adj A]^-1 = adj (A)^-1
(ii) (A^-1)^-1 = A
Solution.
Given, A = \(\left[\begin{array}{rrr}
1 & -2 & 1 \\
-2 & 3 & 1 \\
1 & 1 & 5
\end{array}\right]\)

∴ |A| = 1(5 – 1) + 2(- 10 – 1) + 1 (- 2 – 3) = 14 – 22 – 5 = – 13 ≠ 0
Thus, A is non-singular. Therefore its inverse exists.
Cofactors of A are
A₁₁ = 14,
A₁₂= 11,
A₁₃ = – 5
A₂₁ = 11,
A₂₂ = 4,
A₂₃ = – 3
A₃₁ = – 5
A₃₂ = – 3
A₃₃ = – 1

∴ adj (A) = \(\left[\begin{array}{ccc}
14 & 11 & -5 \\
11 & 4 & -3 \\
-5 & -3 & -1
\end{array}\right]\)

∴ A^-1 = \(\frac{1}{|A|}\) (adj A)
= \(-\frac{1}{13}\left[\begin{array}{ccc}
14 & 11 & -5 \\
11 & 4 & -3 \\
-5 & -3 & -1
\end{array}\right]=\frac{1}{13}\left[\begin{array}{ccc}
-14 & -11 & 5 \\
-11 & -4 & 3 \\
5 & 3 & 1
\end{array}\right]\)

(i) Let B = |adj A|
= 14 (- 4 – 9) – 11(- 11 – 15) – 5(- 33 + 20)
= 14(- 13) – 11(- 26) – 5(- 13)
= – 182 + 286 + 65 = 169 ≠ 0
Cofactors of B are:
B₁₁ = – 13,
B₁₂ = 26,
B₁₃ = – 13,
B₂₁ = 26,
B₂₂ = – 39,
B₂₃ = – 13
B₃₁ = – 13,
B₃₂ = – 13,
B₃₃ = – 65
∴ adj(adjA) = \(\left[\begin{array}{rrr}
-13 & 26 & -13 \\
26 & -39 & -13 \\
-13 & -13 & -65
\end{array}\right]\)
∴ B = [adj A]^-1
= \(\frac{1}{|\ {adj} A|}\) [adj(adj A)]

= \(\frac{1}{169}\left[\begin{array}{rrr}
-13 & 26 & -13 \\
26 & -39 & -13 \\
-13 & -13 & -65
\end{array}\right]=\frac{1}{13}\left[\begin{array}{rrr}
-1 & 2 & -1 \\
2 & -3 & -1 \\
-1 & -1 & -5
\end{array}\right]\) ……………..(i)

Cofactors of A^-1 are
A₁₁ = \(\frac{-13}{169}\)

A₁₂ = \(\frac{26}{169}\)

A₁₃ = \(\frac{-13}{169}\)

A₂₁ = \(\frac{26}{169}\)

A₂₂ = \(\frac{-39}{169}\)

A₂₃ = \(\frac{-13}{169}\)

A₃₁ = \(\frac{-13}{169}\)

A₃₂ = \(\frac{-13}{169}\)

A₃₃ = \(\frac{-65}{169}\)

= \(\frac{1}{169}\left[\begin{array}{ccc}
-13 & 26 & -13 \\
26 & -39 & -13 \\
-13 & -13 & -65
\end{array}\right]=\frac{1}{13}\left[\begin{array}{rrr}
-1 & 2 & -1 \\
2 & -3 & -1 \\
-1 & -1 & -5
\end{array}\right]\) ……………(ii)

From Eqs. (i) and (ii) we get
[adj A]^-1 = adj (A^-1).

(ii) We have shown that
A^-1 = \(\frac{1}{13}\left[\begin{array}{rrr}
-14 & -11 & 5 \\
-11 & -4 & 3 \\
5 & 3 & 1
\end{array}\right]\)

and adj A^-1 = \(\frac{1}{13}\left[\begin{array}{rrr}
-1 & 2 & -1 \\
2 & -3 & -1 \\
-1 & -1 & -5
\end{array}\right]\)
Now, |A^-1| = \(\left(\frac{1}{13}\right)^{3}\) [- 14 × (- 13) + 11 × (- 26) + 5 × (- 13)]
= \(\left(\frac{1}{13}\right)^{3}\) × (- 169) = \(-\frac{1}{13}\)

∴ (A^-1)^-1 = \(\frac{\ {adj} A^{-1}}{\left|A^{-1}\right|}\)

= \(\frac{1}{\left(-\frac{1}{13}\right)} \times \frac{1}{13}\left[\begin{array}{rrr}
-1 & 2 & -1 \\
2 & -3 & -1 \\
-1 & -1 & -5
\end{array}\right]\)

= \(\left[\begin{array}{rrr}
1 & -2 & 1 \\
-2 & 3 & 1 \\
1 & 1 & 5
\end{array}\right]\) = A
∴ (A^-1)^-1 = A.

Question 9.
Evaluate \(\left|\begin{array}{ccc}
x & y & x+y \\
y & x+y & x \\
x+y & x & y
\end{array}\right|\).
Solution.

By expanding along R₁, we have
∆ = 2 (x + y) [- x² + y (x – y)]
= – 2 (x + y) (x² + y² – yx)
= – 2(x³ + y³).

Question 10.
Evaluate \(\left|\begin{array}{ccc}
1 & x & y \\
1 & x+y & y \\
1 & x & x+y
\end{array}\right|\).
Solution.
Let ∆ = \(\left|\begin{array}{ccc}
1 & x & y \\
1 & x+y & y \\
1 & x & x+y
\end{array}\right|\)

App1ying R₂ → R₂ – R₁ and R₃ → R₃ – R₁

∆ = \(\left|\begin{array}{lll}
1 & x & y \\
0 & y & 0 \\
0 & 0 & x
\end{array}\right|\)
By expanding along C₁, we have
∆ = 1(xy – 0) = xy.

DirectIon (11 – 15):
Using ptoperties of determinants, prove that following questions

Question 11.
\(\left|\begin{array}{lll}
\alpha & \alpha^{2} & \beta+\gamma \\
\beta & \beta^{2} & \gamma+\alpha \\
\gamma & \gamma^{2} & \alpha+\beta
\end{array}\right|\) = (β – γ) (γ – α) (α – β) (α + β + γ)
Solution.

By expanding along R₃, we have
= (β – α) (γ – α) [- (γ – β) (- α – β – γ)]
= (β – α) (γ – α) (γ – β)(α + β + γ)
= (α – β) (β – γ) (γ – α) (α + β + γ)
Hence, the given result is proved.

Question 12.
\(\left|\begin{array}{lll}
x & x^{2} & 1+p x^{3} \\
y & y^{2} & 1+p y^{3} \\
z & z^{2} & 1+p z^{3}
\end{array}\right|\) = (1 + pxyz) (x – y) (y – z) (z – x)
Solution.
Let ∆ = \(\left|\begin{array}{lll}
x & x^{2} & 1+p x^{3} \\
y & y^{2} & 1+p y^{3} \\
z & z^{2} & 1+p z^{3}
\end{array}\right|\)
App1ying R₂ → R₂ – R₁ and R₃ → R₃ – R₁

By expanding along R₃, we have
∆ = (x – y) (y – z) (z – x) [(- 1)(p) (xy² + x³ + x²y) + 1 + px³ + p (x + y + z) (xy)]
= (x – y) (y – z) (z – x) [- pxy² – px³ – px²y + 1 + px³ + px²y + pxy² + pxyz]
= (x – y) (y – z) (z – x) (1 + pxyz)
Hence, the given result is proved.

Question 13.
\(\left|\begin{array}{ccc}
3 a & -a+b & -a+c \\
-b+a & 3 b & -b+c \\
-c+a & -c+b & 3 c
\end{array}\right|\) = 3 (a + b + c) (ab + bc + ca)
Solution.

∆ = (a + b + c) \(\left|\begin{array}{ccc}
1 & -a+b & -a+c \\
0 & 2 b+a & a-b \\
0 & a-c & 2 c+a
\end{array}\right|\)
By expanding along C₁, we have
∆ = (a + b + c) [(2b + a) (2c + a) – (a – b) (a – c)]
= (a + b + c) [4bc + 2ab + 2ac + a² – a² + ac + ba – bc]
= (a + b + c) (3ab + 3bc + 3ac)
= 3(a + b + c)(ab + bc + ca)
Hence, the given result is proved.

Question 14.
\(\left|\begin{array}{ccc}
1 & 1+p & 1+p+q \\
2 & 3+2 p & 4+3 p+2 q \\
3 & 6+3 p & 10+6 p+3 q
\end{array}\right|\) = 1
Solution.
Let ∆ = \(\left|\begin{array}{ccc}
1 & 1+p & 1+p+q \\
2 & 3+2 p & 4+3 p+2 q \\
3 & 6+3 p & 10+6 p+3 q
\end{array}\right|\)
Applying R₂ → R₂ 2R₁ and R₃ → R₃ – 3 R₁, we have

∆ = \(\left|\begin{array}{ccc}
1 & 1+p & 1+p+q \\
0 & 1 & 2+p \\
0 & 3 & 7+3 p
\end{array}\right|\)
Applying R₃ → R₃ – 3 R₂, we have

∆ = \(\left|\begin{array}{ccc}
1 & 1+p & 1+p+q \\
0 & 1 & 2+p \\
0 & 0 & 1
\end{array}\right|\)

By expanding along C₁, we have = 1 (1 – 0) = 1.

Question 15.
\(\left|\begin{array}{ccc}
\sin \alpha & \cos \alpha & \cos (\alpha+\delta) \\
\sin \beta & \cos \beta & \cos (\beta+\delta) \\
\sin \gamma & \cos \gamma & \cos (\gamma+\delta)
\end{array}\right|\) = 0
Solution.

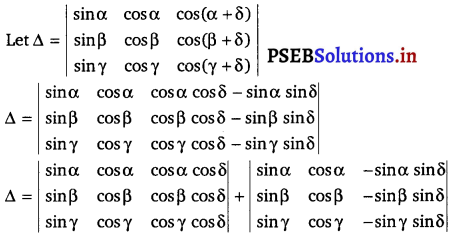
Taking common cos δ from C₃ in first determinant and taking common – sin δ from C₃ in second determinant
∆ = \(\cos \delta\left|\begin{array}{lll}
\sin \alpha & \cos \alpha & \cos \alpha \\
\sin \beta & \cos \beta & \cos \beta \\
\sin \gamma & \cos \gamma & \cos \gamma
\end{array}\right|-\sin \delta\left|\begin{array}{ccc}
\sin \alpha & \cos \alpha & \sin \alpha \\
\sin \beta & \cos \beta & \sin \beta \\
\sin \gamma & \cos \gamma & \sin \gamma
\end{array}\right|\)
∆ = cos δ . 0 – sin δ . 0 = 0
[Since, C₂ and C₃ in first determinant C₁ and C₃ in second determinant are identical so values of determinants are zero.]
Hence, the given result is proved.

Question 16.
Solve the system of the following equations
\(\frac{2}{x}+\frac{3}{y}+\frac{10}{z}\) = 4; \(\frac{4}{x}-\frac{6}{y}+\frac{5}{z}\) = 1; \(\frac{6}{x}+\frac{9}{y}-\frac{20}{x}\) = 2
Solution.
Let \(\frac{1}{x}\) = p, \(\frac{1}{y}\) = q, \(\frac{1}{z}\) = r.
Then, the given system of equation is as follows:
2p + 3q + 10r = 4, 4p – 6q + 5r = 1, 6p + 9q – 20 = 2.
This system can be written in the form of AX = B, where

A = \(\left[\begin{array}{ccc}
2 & 3 & 10 \\
4 & -6 & 5 \\
6 & 9 & -20
\end{array}\right]\), X = \(\left[\begin{array}{l}
p \\
q \\
r
\end{array}\right]\) and B = \(\left[\begin{array}{l}
4 \\
1 \\
2
\end{array}\right]\)

Now, |A| = 2(120 – 45) – 3(- 80 – 30) + 10 (36 + 36)
= 150 + 330 + 720 = 1200
Thus, A is non-singular. Therefore, its inverse exists.
Cofactors of A are
A₁₁ = 75,
A₁₂ = 110,
A₁₃ = 72,
A₂₁ = 150,
A₂₂ = – 100,
A₂₃ = 0,
A₃₁ = 7,
A₃₂ = 30,
A₃₃ = – 24

= \(\frac{1}{1200}\left[\begin{array}{c}
300+150+150 \\
440-100+60 \\
288+0-48
\end{array}\right]=\frac{1}{1200}\left[\begin{array}{c}
600 \\
400 \\
240
\end{array}\right]=\left[\begin{array}{l}
\frac{1}{2} \\
\frac{1}{3} \\
\frac{1}{5}
\end{array}\right]\)

∴ p = \(\frac{1}{2}\), q = \(\frac{1}{3}\) and r = \(\frac{1}{5}\)
⇒ \(\frac{1}{x}=\frac{1}{2}\), \(\frac{1}{y}=\frac{1}{3}\), \(\frac{1}{z}=\frac{1}{5}\)
Hence x = 2, y = 3 and z = 5.

Direction (17 – 19): Choose the correct answer in the following questions.

Question 17.
If a, b and c are in AP., then the determinant \(\left|\begin{array}{lll}
x+2 & x+3 & x+2 a \\
x+3 & x+4 & x+2 b \\
x+4 & x+5 & x+2 c
\end{array}\right|\) is
(A) 0
(B) 1
(C) x
(D) 2x
Solution.

Question 18.
If x, y and z are non-zero real numbers, then the inverse of matrix A = \(\left[\begin{array}{lll}
x & 0 & 0 \\
0 & y & 0 \\
0 & 0 & z
\end{array}\right]\) is
(A) \(\left[\begin{array}{ccc}
x^{-1} & 0 & 0 \\
0 & y^{-1} & 0 \\
0 & 0 & z^{-1}
\end{array}\right]\)

(B) xyz \(\left[\begin{array}{ccc}
x^{-1} & 0 & 0 \\
0 & y^{-1} & 0 \\
0 & 0 & z^{-1}
\end{array}\right]\)

(C) \(\frac{1}{x y z}\left[\begin{array}{ccc}
x & 0 & 0 \\
0 & y & 0 \\
0 & 0 & z
\end{array}\right]\)

(D) \(\frac{1}{x y z}\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)
solution.
Given, A = \(\left[\begin{array}{lll}
x & 0 & 0 \\
0 & y & 0 \\
0 & 0 & z
\end{array}\right]\)
∴ |A| = x (yz – 0) = xyz ≠ 0
(∵ x, y, z are non-zero)
Cofactors of A are
A₁₁ = yz,
A₁₂ = 0,
A₁₃ = 0
A₂₁ = 0,
A₂₂ = xz,
A ₂₃= 0
A₃₁ = 0,
A₃₂ = 0,
A₃₃ = xy

Hence, the correct answer is (A).

Question 19.
Let A = \(\left[\begin{array}{ccc}
1 & \sin \theta & 1 \\
-\sin \theta & 1 & \sin \theta \\
-1 & -\sin \theta & 1
\end{array}\right]\), where 0 ≤ θ ≤ 2π, then
(A) Det (A) = 0
(B) Det (A) ∈ (2, ∞)
(C) Det (A) ∈(2, 4)
(D)Det (A) ∈ [2, 4]
Solution.
Given, A = \(\left[\begin{array}{ccc}
1 & \sin \theta & 1 \\
-\sin \theta & 1 & \sin \theta \\
-1 & -\sin \theta & 1
\end{array}\right]\)

∴ |A| = 1 (1 + sin² θ) – sin θ (- sin θ + sin θ) – 1 (sin² θ + 1)
= 1 + sin² θ + sin² θ + 1
= 2 + 2 sin² θ
= 2 (1 + sin² θ)
Now, 0 ≤ θ ≤ 2π
= 0 ≤ sin θ ≤ 1
= 0 ≤ sin² θ ≤ 1
= 1 ≤ 1 + sin² θ ≤ 2
= 2 ≤ 2 (1 + sin² θ) ≤ 4
∴ Det (A) ∈ [2, 4]
Hence, the correct answer is (D).