PSEB 12th Class Maths Solutions Chapter 5 Continuity and Differentiability Ex 5.2

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 5 Continuity and Differentiability Ex 5.2 Textook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.2

Direction (1 – 8): Differentiate the following functions with respect to x.

Question 1.
sin(x² + 5)
Solution.
The given function is sin(x² + 5)
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\) [sin(x² + 5)] = cos(x² + 5) \(\frac{d}{d x}\) (x2 + 5)
= cos (x² + 5) [\(\frac{d}{d x}\) (x² + \(\frac{d}{d x}\) (5)]
= cos (x² + 5) . [2x + 0]
= 2x cos(x² + 5)

Question 2.
cos(sin x)
Solution.
The given function is cos(sinx)
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\) [cos(sin x)] = – sin(sin x) . \(\frac{d}{d x}\) (sin x)
= – sin(sin x) . cos x
= – cos x sin(sin x)

Question 3.
sin(ax + b)
Solution.
The given function is sin(ax + b)
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\) [sin (ax + b)] = cos(ax + b) \(\frac{d}{d x}\) (ax + b)
= cos (ax + b) . [\(\frac{d}{d x}\) (ax) + \(\frac{d}{d x}\) (b)]
= cos(ax + b) . (a + 0)
= a cos (ax + b)

Question 4.
sec(tan √x)
Solution.
The given function is sec (tan (√x))
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\) [sec(tan √x)] = sec (tan √x) . tan(tan √x) (tan √x) . \(\frac{d}{d x}\) (tan √x)
= sec(tan √x) . tan(tan √x) sec² (√x). \(\frac{d}{d x}\) (√x)
= sec(tan √x) . tan(tan √x) . sec² (√x) . \(\frac{1}{2 \sqrt{x}}\)
= \(\frac{\sec (\tan \sqrt{x}) \cdot \tan (\tan \sqrt{x}) \cdot \sec ^{2}(\sqrt{x})}{2 \sqrt{x}}\).

Question 5.
\(\frac{\sin (a x+b)}{\cos (c x+d)}\)
Solution.
Let y = \(\frac{\sin (a x+b)}{\cos (c x+d)}=\frac{u}{v}\)
u = sin (ax + b)
differentiating w.r.t. x, we get
\(\frac{d u}{d x}\)= cos (ax + b) \(\frac{d}{d x}\) (ax + b) = a cos (ax + b)
v = cos (cx + d)
differentiating w.r.t. x, we get
\(\frac{d v}{d x}\) = – sin (cx + d) \(\frac{d}{d x}\) (cx + d)
= – sin (cx + d) × c
= – c sin (cx + d)

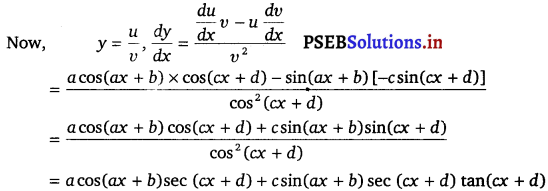
Question 6.
cos x³ . sin² (x⁵)
Sol.
The given function is cos x³ . sin² (x⁵)
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\) [cos x³ . sin² (x⁵)] = sin ² (x⁵) × \(\frac{d}{d x}\) (cos x³) + cos x³ × \(\frac{d}{d x}\) [sin² (x⁵)]

= sin² (x⁵) × (- sin x³) × \(\frac{d}{d x}\) (x³) + cos x³ x 2 sin (x⁵) – (sin x⁵)

= – sin x³ sin² (x⁵) × 3x² + 2 sin x⁵ cos x³ cos x⁵ × \(\frac{d}{d x}\) (x⁵)

= – 3x² sin x³ sin² (x⁵) + 2 sin x⁵ cos x⁵ cos x³ . 5x⁴
= x² sin x⁵ (- 3 sin x³ sin x⁵ + 10x² cos x³ cos x⁵).

Question 7.
2 \(\sqrt{\cot \left(x^{2}\right)}\)
Solution.
The given function is 2 \(\sqrt{\cot \left(x^{2}\right)}\)
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\left[2 \sqrt{\cot \left(x^{2}\right)}\right]=2 \cdot \frac{1}{2 \sqrt{\cot \left(x^{2}\right)}} \times \frac{d}{d x}\left[\cot \left(x^{2}\right)\right]\)

Question 8.
cos (√x)
Solution.
The given function is cos(√x)
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\) [cos (√x)] = – sin(√x) . \(\frac{d}{d x}\) (√x)
= \(-\sin (\sqrt{x}) \times \frac{d}{d x}\left(x^{\frac{1}{2}}\right)=-\sin \sqrt{x} \times \frac{1}{2} x^{-\frac{1}{2}}=\frac{-\sin \sqrt{x}}{2 \sqrt{x}}\)

Question 9.
Prove that the function f given by f(x) =|x – 1|, x ∈ R is not differentiable at x = 1.
Solution.
The given function may be written as
f(x) =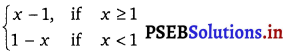
RHD = Right hand derivative at x = 1
= \(\lim _{h \rightarrow 0} \frac{f(1+h)-f(1)}{h}=\lim _{h \rightarrow 0} \frac{[(1+h)-1]-(1-1)}{h}\)

= \(\lim _{h \rightarrow 0} \frac{h}{h}\) = 1

LHD = Left hand derivative at x = 1
= \(\lim _{h \rightarrow 0} \frac{f(1-h)-f(1)}{-h}=\lim _{h \rightarrow 0} \frac{1-(1-h)-(1-1)}{-h}\)

= \(\lim _{h \rightarrow 0} \frac{h}{-h}\) = – 1

RHD ≠ LHD
⇒ f is not differentiable at x = 1.

Question 10.
Prove that the greatest integer function defined by f(x) = [x], 0 < x < 3 is not differentiable at x – 1 and x = 2.
Solution.
The given function f is f(x) – [x], 0 < x < 3.
It is known that a function f is differentiable at a point x = c in its domain if both
\(\lim _{h \rightarrow 0^{-}} \frac{f(c+h)-f(c)}{h}\) and lim \(\lim _{h \rightarrow 0^{+}} \frac{f(c+h)-f(c)}{h}\) are finite and equal.

To check the differentiability of the given function at x = 1, consider the left hand limit of / at x = 1.

Since, the left and right hand limits of f at x = 1 are not equal, therefore, f is not differentiable at x = 1.
To check the differentiability of the given function at x = 2, consider the left hand limit of f at x = 2.

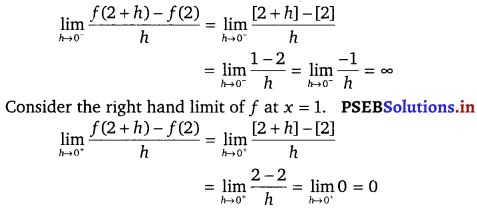
Since, the left and right hand limits of f at x = 2 are not equal, therefore, f is not differentiable at x = 2.