Punjab State Board PSEB 12th Class Religion Book Solutions Chapter 8 जैन धर्म की नैतिक शिक्षाएँ Textbook Exercise Questions and Answers.
PSEB Solutions for Class 12 Religion Chapter 8 जैन धर्म की नैतिक शिक्षाएँ
दीर्घ उत्तरीय प्रश्न-
प्रश्न 1.
जैन धर्म के आरंभ के बारे आप क्या जानते हैं ? वर्णन करो। (What do you know about the origin of Jainism ? Explain.)
उत्तर-
जैन धर्म भारत के सबसे प्राचीन धर्मों में से एक है। इसका साधुओं वाला मार्ग और योग की रीतियों का आरंभ हड़प्पा काल में से ढूँढा जा सकता है। वैदिक साहित्य में जैन आचार्यों का वर्णन मिलता है। इससे पता चलता है कि जैन धर्म उस समय प्रचलित था। जैन अनुश्रुतियों के अनुसार ऋषभनाथ जो कि उनका पहला तीर्थंकर था वह पहला व्यक्ति था जिससे मनुष्य की सभ्यता का आरंभ हुआ। इस तरह सभ्यता के आरंभ के समय पर ही जैन धर्म मौजूद था।
जैन शब्द संस्कृत के शब्द जिन से निकला है जिससे भाव है विजेता। विजेता से भाव उस व्यक्ति से है जिसने अपनी इंद्रियों और मन को जीत लिया हो। जैन धर्म को आरंभ में निरग्रंथ के नाम से जाना जाता है। निरग्रंथ से भाव था बंधनों से रहित अथवा मुक्त। जैन आचार्यों को तीर्थंकर भी कहा जाता है। तीर्थंकर से भाव है पुल बनाने वाला अथवा संसार के भवसागर से पार करने वाला गुरु। जैन दर्शन को अर्हत दर्शन भी कहा जाता है। अर्हत से भाव है पूजनीय। जैन धर्म को मानने वाले जैनी कहलाते हैं। जैन 24 तीर्थंकरों में विश्वास रखते हैं। इनके नाम ये हैं:—
- ऋषभनाथ
- अजित
- संभव
- अभिनंदन
- सुमति
- पद्मप्रभु
- सुपार्श्व
- चंद्रप्रभु
- पुष्पदंत
- शीतल
- श्रेयांसम
- वासुपूज्य
- विमल
- अनंत
- धर्म
- शाँति
- कुंथ
- अरह
- मल्लि
- मुनिसुव्रत
- नामि
- नेमि
- पार्श्वनाथ
- महावीर
जैनी ऋषभनाथ को जैन धर्म का संस्थापक मानते हैं। जैन अनुश्रुतियों के अनुसार उनका जन्म अयोध्या में हुआ। उन्होंने कई वर्षों तक राज्य किया। बाद में उन्होंने अपना राज्य अपने पुत्र भरत को सौंप दिया और स्वयं संसार त्याग कर तपस्या में लग गये। अंत में उनको ज्ञान प्राप्त हुआ। उन्होंने इस ज्ञान के बारे लोगों को उपदेश दिया। इस तरह वह पहले तीर्थंकर कहलाये। ऋषभनाथ के बाद होने वाले 21 तीर्थंकरों को ऐतिहासिक बताना संभव नहीं है, परंतु जैनियों की पवित्र अनुश्रुतियों में इनका वर्णन आता है। जैन धर्म के 23वें तीर्थंकर पार्श्वनाथ और 24वें तीर्थंकर महावीर ऐतिहासिक व्यक्ति थे। स्वामी पार्श्वनाथ का जन्म स्वामी महावीर के जन्म से 250 वर्ष पहले बनारस के राजा अश्वसेन के घर हुआ था। उनकी माता जी का नाम वामादेवी था। उनका बचपन बहुत ही ऐश-ओ-आराम में बीता। 30 वर्षों की आयु में पार्श्वनाथ ने अपने सारे सुखों का त्याग कर दिया और सच्चे ज्ञान की खोज में निकल गये। उनको 83 दिनों के घोर तप के बाद परम ज्ञान प्राप्त हुआ। इसके बाद उन्होंने अपने जीवन के बाकी 70 वर्ष अपने उपदेशों का प्रचार करने में व्यतीत किये। 777 ई० पू० के लगभग उन्होंने बिहार के माऊंट समेता नामक पहाड़ी पर निर्वाण प्राप्त किया। पार्श्वनाथ की शिक्षा को चार्तुयाम अथवा चार प्रण कहते हैं। यह चार प्रण ये हैं—
- सजीव वस्तुओं को कष्ट न पहुँचायें (अहिंसा)।
- झूठ न बोलो (सुनृत)।
- बिना दिये कुछ न लो (अस्तेय)।
- सांसारिक पदार्थों से मोह न करो (अपरिग्रह)।
स्वामी महावीर ने इन चार असूलों में एक और असूल जोड़ा जिसको ब्रह्मचर्य कहा जाता है। इससे यह सिद्ध होता है कि स्वामी महावीर जैन धर्म के संस्थापक नहीं बल्कि सुधारक थे।

प्रश्न 2.
(क) जैन धर्म में कुल कितने तीर्थंकर हुए हैं ?
(ख) भगवान् महावीर के जीवन पर प्रकाश डालें।
[(a) Give the total number of Tirthankaras in Jainism.
(b) Throw light on the life of Lord Mahavira.]
अथवा
महावीर की माता का क्या नाम था ? भगवान् महावीर के जन्म से पहले उनकी माता को कितने स्वप्न आए थे? भगवान महावीर के जीवन पर एक नोट लिखें।
(Give the name of Mahavir as mother. How many dreams Lord Mehavira’s mother had before giving birth to Mahavira ? Write a note on the life of Lord Mahavira.)
अथवा
जैन धर्म में कितने तीर्थंकर हुए हैं ? 24वें तीर्थंकर के जीवन पर नोट लिखें।
(Give the number of Tirthankaras in Jainism. Write a note on the life of 24th Tirthankara.)
अथवा
भगवान् महावीर जैन धर्म के कौन से तीर्थंकर थे ? उनके जीवन के संबंध में जानकारी दें।
(What was Lord Mahavira’s number among Jain Tirthankaras ? Write about Mahavira’s life.)
उत्तर-
जैन धर्म में कुल 24 तीर्थंकर हुए हैं। 24वें तीर्थंकर स्वामी महावीर के जीवन का संक्षिप्त वर्णन निम्नलिखित अनुसार है—

LORD MAHAVIRA
1. महावीर का जन्म और बचपन (Birth and Childhood of Mahavira)- महावीर का जन्म 599 ई० पू० वैशाली (बिहार) के नज़दीक कुंडग्राम में हुआ। कुछ इतिहासकार उनकी जन्म तिथि 540 ई० पू० बताते हैं। महावीर के बचपन का नाम वर्धमान था। महावीर जी के पिता जी का नाम सिद्धार्थ था और वह एक क्षत्रिय कबीले जनत्रिका के मुखिया थे। महावीर जी की माता जी का नाम तृषला था। वह लिच्छवी वंश के शासक चेटक की बहन थी। भगवान् महावीर के जन्म से पूर्व उसे 14 स्वप्न आए थे। महावीर को शिक्षा देने के लिए विशेष प्रबंध किये गये थे। महावीर जी का बचपन से ही सांसारिक वस्तुओं से कोई लगाव नहीं था। वह अपने ही विचारों में डूबे रहते थे।
2. विवाह (Marriage)—सांसारिक कार्यों की ओर महावीर जी का ध्यान लगाने के लिए उनके पिता जी ने महावीर का विवाह एक सुंदर राजकुमारी यशोदा से कर दिया। विवाह के समय महावीर जी की आयु कितनी थी इसके बारे हमें कोई निश्चित जानकारी प्राप्त नहीं है। कुछ समय पश्चात् महावीर जी के घर एक पुत्री ने जन्म लिया। उसका नाम प्रियादर्शना रखा गया।
3. महान् त्याग और ज्ञान प्राप्ति (Renunciation and Enlightenment)-गृहस्थी जीवन भी महावीर जी की धार्मिक रुचियों की राह में किसी तरह की अड़चन (रुकावट) न बन सका। अपने माता-पिता की मृत्यु हो जाने के बाद महावीर अपने बड़े भाई नंदीवर्मन से आज्ञा लेकर गृह त्याग्न कर जंगलों में ज्ञान की खोज के लिए चले गये। उस समय महावीर जी की आयु 30 वर्ष थी। उन्होंने 12 वर्षों तक बड़ा कठोर तप किया। अंततः उनको ऋजुपालिका नदी के नज़दीक जरिमबिक गाँव में कैवल्य ज्ञान (सर्वोच्च सत्य) प्राप्त हुआ। इस ज्ञान की प्राप्ति के बाद वर्धमान जिन (इंद्रियों पर जीत प्राप्त करने वाला) और महावीर (महान् विजयी) कहलाये। ज्ञान प्राप्ति के समय महावीर जी की आयु 42 वर्ष थी।
4. धर्म प्रचार (Preachings)-ज्ञान प्राप्ति के बाद महावीर जी ने लोगों में फैले अंधविश्वासों को दूंर करने के लिए और उनको सच्चा मार्ग बताने के लिए अपने उपदेशों का प्रचार किया। उनके उपदेशों से बहुत सारे लोग प्रभावित हुए और वे महावीर जी के अनुयायी बन गये। महावीर जी के प्रसिद्ध प्रचार केंद्र राजगृह, वैशाली, कौशल, मिथिला, विदेह और अंग थे। जैन परंपराओं के अनुसार मगध के शासक बिंबिसार और उसके पुत्र अजातशत्रु ने जैन मत को स्वीकार कर लिया।
5. निर्वाण (Nirvana)—स्वामी महावीर ने लगभग 30 वर्षों तक अपना प्रचार किया। 72 वर्ष की आयु में पावा (पटना) में 527 ई० पू० में उन्होंने निर्वाण (मुक्ति) प्राप्त किया। उस समय महावीर जी के 14,000 अनुयायी थे।
प्रश्न 3.
जैन धर्म के आरंभ तथा विकास के बारे में प्रकाश डालें। (Discuss the origin and development of Jainism.)
अथवा
जैन धर्म के बारे में जानकारी दीजिए।
(Describe Jainism.)
उत्तर-
जैन धर्म भारत के सबसे प्राचीन धर्मों में से एक है। इसका साधुओं वाला मार्ग और योग की रीतियों का आरंभ हड़प्पा काल में से ढूँढा जा सकता है। वैदिक साहित्य में जैन आचार्यों का वर्णन मिलता है। इससे पता चलता है कि जैन धर्म उस समय प्रचलित था। जैन अनुश्रुतियों के अनुसार ऋषभनाथ जो कि उनका पहला तीर्थंकर था वह पहला व्यक्ति था जिससे मनुष्य की सभ्यता का आरंभ हुआ। इस तरह सभ्यता के आरंभ के समय पर ही जैन धर्म मौजूद था।
जैन शब्द संस्कृत के शब्द जिन से निकला है जिससे भाव है विजेता। विजेता से भाव उस व्यक्ति से है जिसने अपनी इंद्रियों और मन को जीत लिया हो। जैन धर्म को आरंभ में निरग्रंथ के नाम से जाना जाता है। निरग्रंथ से भाव था बंधनों से रहित अथवा मुक्त। जैन आचार्यों को तीर्थंकर भी कहा जाता है। तीर्थंकर से भाव है पुल बनाने वाला अथवा संसार के भवसागर से पार करने वाला गुरु। जैन दर्शन को अर्हत दर्शन भी कहा जाता है। अर्हत से भाव है पूजनीय। जैन धर्म को मानने वाले जैनी कहलाते हैं। जैन 24 तीर्थंकरों में विश्वास रखते हैं। इनके नाम ये हैं:—
- ऋषभनाथ
- अजित
- संभव
- अभिनंदन
- सुमति
- पद्मप्रभु
- सुपार्श्व
- चंद्रप्रभु
- पुष्पदंत
- शीतल
- श्रेयांसम
- वासुपूज्य
- विमल
- अनंत
- धर्म
- शाँति
- कुंथ
- अरह
- मल्लि
- मुनिसुव्रत
- नामि
- नेमि
- पार्श्वनाथ
- महावीर
जैनी ऋषभनाथ को जैन धर्म का संस्थापक मानते हैं। जैन अनुश्रुतियों के अनुसार उनका जन्म अयोध्या में हुआ। उन्होंने कई वर्षों तक राज्य किया। बाद में उन्होंने अपना राज्य अपने पुत्र भरत को सौंप दिया और स्वयं संसार त्याग कर तपस्या में लग गये। अंत में उनको ज्ञान प्राप्त हुआ। उन्होंने इस ज्ञान के बारे लोगों को उपदेश दिया। इस तरह वह पहले तीर्थंकर कहलाये। ऋषभनाथ के बाद होने वाले 21 तीर्थंकरों को ऐतिहासिक बताना संभव नहीं है, परंतु जैनियों की पवित्र अनुश्रुतियों में इनका वर्णन आता है। जैन धर्म के 23वें तीर्थंकर पार्श्वनाथ और 24वें तीर्थंकर महावीर ऐतिहासिक व्यक्ति थे। स्वामी पार्श्वनाथ का जन्म स्वामी महावीर के जन्म से 250 वर्ष पहले बनारस के राजा अश्वसेन के घर हुआ था। उनकी माता जी का नाम वामादेवी था। उनका बचपन बहुत ही ऐश-ओ-आराम में बीता। 30 वर्षों की आयु में पार्श्वनाथ ने अपने सारे सुखों का त्याग कर दिया और सच्चे ज्ञान की खोज में निकल गये। उनको 83 दिनों के घोर तप के बाद परम ज्ञान प्राप्त हुआ। इसके बाद उन्होंने अपने जीवन के बाकी 70 वर्ष अपने उपदेशों का प्रचार करने में व्यतीत किये। 777 ई० पू० के लगभग उन्होंने बिहार के माऊंट समेता नामक पहाड़ी पर निर्वाण प्राप्त किया। पार्श्वनाथ की शिक्षा को चार्तुयाम अथवा चार प्रण कहते हैं। यह चार प्रण ये हैं—
- सजीव वस्तुओं को कष्ट न पहुँचायें (अहिंसा)।
- झूठ न बोलो (सुनृत)।
- बिना दिये कुछ न लो (अस्तेय)।
- सांसारिक पदार्थों से मोह न करो (अपरिग्रह)।
स्वामी महावीर ने इन चार असूलों में एक और असूल जोड़ा जिसको ब्रह्मचर्य कहा जाता है। इससे यह सिद्ध होता है कि स्वामी महावीर जैन धर्म के संस्थापक नहीं बल्कि सुधारक थे।
1. महावीर का जन्म और बचपन (Birth and Childhood of Mahavira)- महावीर का जन्म 599 ई० पू० वैशाली (बिहार) के नज़दीक कुंडग्राम में हुआ। कुछ इतिहासकार उनकी जन्म तिथि 540 ई० पू० बताते हैं। महावीर के बचपन का नाम वर्धमान था। महावीर जी के पिता जी का नाम सिद्धार्थ था और वह एक क्षत्रिय कबीले जनत्रिका के मुखिया थे। महावीर जी की माता जी का नाम तृषला था। वह लिच्छवी वंश के शासक चेटक की बहन थी। भगवान् महावीर के जन्म से पूर्व उसे 14 स्वप्न आए थे। महावीर को शिक्षा देने के लिए विशेष प्रबंध किये गये थे। महावीर जी का बचपन से ही सांसारिक वस्तुओं से कोई लगाव नहीं था। वह अपने ही विचारों में डूबे रहते थे।
2. विवाह (Marriage)—सांसारिक कार्यों की ओर महावीर जी का ध्यान लगाने के लिए उनके पिता जी ने महावीर का विवाह एक सुंदर राजकुमारी यशोदा से कर दिया। विवाह के समय महावीर जी की आयु कितनी थी इसके बारे हमें कोई निश्चित जानकारी प्राप्त नहीं है। कुछ समय पश्चात् महावीर जी के घर एक पुत्री ने जन्म लिया। उसका नाम प्रियादर्शना रखा गया।
3. महान् त्याग और ज्ञान प्राप्ति (Renunciation and Enlightenment)-गृहस्थी जीवन भी महावीर जी की धार्मिक रुचियों की राह में किसी तरह की अड़चन (रुकावट) न बन सका। अपने माता-पिता की मृत्यु हो जाने के बाद महावीर अपने बड़े भाई नंदीवर्मन से आज्ञा लेकर गृह त्याग्न कर जंगलों में ज्ञान की खोज के लिए चले गये। उस समय महावीर जी की आयु 30 वर्ष थी। उन्होंने 12 वर्षों तक बड़ा कठोर तप किया। अंततः उनको ऋजुपालिका नदी के नज़दीक जरिमबिक गाँव में कैवल्य ज्ञान (सर्वोच्च सत्य) प्राप्त हुआ। इस ज्ञान की प्राप्ति के बाद वर्धमान जिन (इंद्रियों पर जीत प्राप्त करने वाला) और महावीर (महान् विजयी) कहलाये। ज्ञान प्राप्ति के समय महावीर जी की आयु 42 वर्ष थी।
4. धर्म प्रचार (Preachings)-ज्ञान प्राप्ति के बाद महावीर जी ने लोगों में फैले अंधविश्वासों को दूंर करने के लिए और उनको सच्चा मार्ग बताने के लिए अपने उपदेशों का प्रचार किया। उनके उपदेशों से बहुत सारे लोग प्रभावित हुए और वे महावीर जी के अनुयायी बन गये। महावीर जी के प्रसिद्ध प्रचार केंद्र राजगृह, वैशाली, कौशल, मिथिला, विदेह और अंग थे। जैन परंपराओं के अनुसार मगध के शासक बिंबिसार और उसके पुत्र अजातशत्रु ने जैन मत को स्वीकार कर लिया।
5. निर्वाण (Nirvana)—स्वामी महावीर ने लगभग 30 वर्षों तक अपना प्रचार किया। 72 वर्ष की आयु में पावा (पटना) में 527 ई० पू० में उन्होंने निर्वाण (मुक्ति) प्राप्त किया। उस समय महावीर जी के 14,000 अनुयायी थे।

प्रश्न 4.
जैन धर्म की बुनियाद नैतिक शिक्षाएँ हैं चर्चा करो।
(“Ethical teachings are the foundation of Jainism.” Discuss.)
अथवा
जैन धर्म की नैतिक शिक्षाओं के विषय में जानकारी दीजिए। (Describe the Ethical teachings of Jainism.)
अथवा
जैन धर्म की बुनियादी शिक्षाओं के विषय में संक्षिप्त परंतु भावपूर्ण जानकारी दीजिए।
(Describe in brief but meaningful the basic teachings of Jainism.)
अथवा
“नैतिक मूल्य जैन धर्म का आधार हैं।” प्रकाश डालिए।
(“Moral values are the basis of Jainism.” Elucidate.)
अथवा
जैन सदाचार पर एक विस्तृत नोट लिखो।
(Write a detailed note on Jain Ethics. )
अथवा
जैन धर्म के सदाचारक गुणों संबंधी जानकारी दो। (Discuss the Ethical values of Jainism.)
अथवा
जैन धर्म की प्रमुख शिक्षाओं की चर्चा करो।
(Discuss the main teachings of Jainism.)
अथवा
जैन धर्म की नैतिक शिक्षाओं संबंधी जानकारी दो। (Give information about moral teachings of Jainism.)
अथवा
भगवान् महावीर की नैतिक शिक्षाओं के बारे में जानकारी दीजिए। (Describe the Ethical teachings of Lord Mahavira.)
अथवा
जैन धर्म की शिक्षाओं के बारे में बताएँ।
(Write the teachings of Jainism.)
अथवा
जैन धर्म की नैतिक कीमतों के बारे में जानकारी दीजिए।
(Describe the Ethical values of Jainism.)
अथवा
जैन धर्म की नैतिक शिक्षाओं के बारे में चर्चा कीजिए। (Discuss about the Ethical teachings of Jainism.)
अथवा
भगवान् महावीर की मूल शिक्षाओं के बारे में जानकारी दीजिए। (Describe the basic teachings of Lord Mahavira.)
अथवा
जैन धर्म की मुख्य सदाचारक कीमतें कौन-सी हैं ? प्रकाश डालें। (What were the main Ethical values of Jainism ? Elucidate.)
अथवा
जैन धर्म की सदाचारक शिक्षाओं के बारे में जानकारी दीजिए। (Describe the Ethical teachings of Jainism.)
उत्तर-
जैन धर्म की अथवा महावीर जी की मुख्य नैतिक शिक्षाओं ने भारतीय संस्कृति को एक ऐसी देन दी जिस पर हमें आज भी गर्व है। जैन धर्म ने लोगों को त्रि-रत्न, अहिंसा, शुद्ध आचरण और आपसी भाइचारे का पाठ पढ़ाया। इसने समाज में प्रचलित अंध-विश्वासों का जोरदार शब्दों में खंडन किया। इसका यज्ञों, बलियों, वेदों और संस्कृत भाषा की पवित्रता में कोई विश्वास नहीं था। इसने मनुष्य को सादा और पवित्र जीवन व्यतीत करने की प्रेरणा दी। निस्संदेह जैन धर्म की नैतिक शिक्षाओं ने भारतीय समाज को एक नई दिशा देने का एक महान् कार्य किया।—
1. त्रि-रत्न (Tri-Ratna)-जैन धर्म के अनुसार मनुष्य के जीवन का परम उद्देश्य मोक्ष अथवा निर्वाण प्राप्त करना है। इसको प्राप्त करने के लिए जैन धर्म के अनुसार प्रत्येक व्यक्ति के लिए त्रि-रत्नों पर चलना अति ज़रूरी है। ये तीन रत्न हैं-सच्चा विश्वास, सच्चा ज्ञान और सच्चा आचार। पहले रत्न के अनुसार प्रत्येक व्यक्ति को 24 तीर्थंकरों, नौ सच्चाइयों और जैन शास्त्रों में अटल विश्वास होना चाहिए। दूसरे रत्नानुसार जैनियों को सच्चा और पूर्ण ज्ञान प्राप्त करना चाहिए। यह तीर्थंकरों के उपदेशों के गहरे अध्ययन से प्राप्त होता है। इस ज्ञान के दो रूप बताये गये हैं जिनको प्रत्यक्ष और परोक्ष ज्ञान कहा जाता है। आत्मा द्वारा प्राप्त ज्ञान को प्रत्यक्ष ज्ञान कहते हैं और वह ज्ञान जो इंद्रियों के द्वारा प्राप्त होता है उसको परोक्ष ज्ञान कहा जाता है। ज्ञान की पाँच किस्में हैं, जिनके नाम इस तरह हैं-मति ज्ञान, श्रुति ज्ञान, अवधि ज्ञान, मनपर्याय ज्ञान और केवल्य ज्ञान। तीसरे रत्नानुसार प्रत्येक व्यक्ति को सच्चे आचार के अनुसार अपना जीवन व्यतीत करना चाहिए। सच्चा आचार वह है जिसकी शिक्षा जैन धर्म देता है। ये तीनों रत्न साथ-साथ चलते हैं। इनमें से किसी एक की अनुपस्थिति मनुष्य को उसकी मंजिल तक नहीं पहुँचा सकती। उदाहरण के तौर पर जैसे एक दीये को प्रकाश देने के लिए उसमें तेल, बाती और आग का होना ज़रूरी है। यदि इसमें से एक भी वस्तु की कमी हो तो वह प्रकाश नहीं दे सकता।
2. अहिंसा (Ahimsa)-जैन धर्म में अहिंसा पर बहुत जोर दिया गया है। अहिंसा की महत्ता बताते हुए आचारांग सूत्र में कहा गया है, “सभी को अपना-अपना जीवन प्यारा है, सब ही सुख चाहते हैं, दुःख कोई नहीं चाहता, अधिक कोई नहीं चाहता, सब को जीवन प्यारा है और सारे ही जीने की इच्छा रखते हैं।” इसीलिए जो हमारे लिए सुखमयी है वह दूसरों के लिए भी सुखमयी है। हिंसा दो तरह की होती है-मन से हिंसा और कर्म से हिंसा। कर्म अथवा अमल में आने वाली हिंसा से पहले मन भाव विचारों में हिंसा आती है। गुस्सा, अहंकार, लालच और धोखा मन की हिंसा है। इसलिए हिंसा से बचने के लिए मन के विचारों को शुद्ध करना अति ज़रूरी है। जैन धर्म के अनुसार मनुष्यों के अतिरिक्त पशुओं, पत्थरों और वृक्षों आदि में भी आत्मा निवास करती है। इसलिए हमें किसी जीव या निर्जीव को कष्ट नहीं देना चाहिए। इसी कारण जैनी लोग नंगे पाँव चलते हैं, मुँह पर पट्टी बाँधते हैं, पानी छान कर पीते हैं और अंधेरा हो जाने के बाद कुछ नहीं खाते ताकि किसी जीव की हत्या न हो जाये। बी० एन० लूनीया के अनुसार,
“अहिंसा जैन धर्म की आधारशिला है।”1
3. नौ सच्चाइयाँ (Nine Truths)-जैन दर्शन नौ सच्चाइयों की शिक्षा देता है। ये सच्चाइयाँ हैं(1) जीव-जैन दर्शन में आत्मा को जीव कहा गया है। यह चेतन सुरूप है। यह शरीर के कर्मों के अच्छे-बुरे फल भुगतता है और आवागमन के चक्र में पड़ता है। (2) अजीव-यह जंतु पदार्थ है। यह निर्जीव है और इनमें समझ नहीं होती। इनकी दो श्रेणियाँ हैं रूपी और अरूपी। (3) पुण्य-यह अच्छे कर्मों का नतीजा है। इसके नौ साधन हैं। (4) पाप-यह जीव के बंधन का मुख्य कारण है। इसके परिणामस्वरूप घोर सज़ायें मिलती हैं। (5) अशर्व-यह वह प्रक्रिया है जिसके अनुसार आत्मा अपने अंदर कर्मों को संचित करती रहती है। कर्म 8 किस्मों के होते हैं। (6) संवर-कर्म को आत्मा की ओर आने की क्रिया को रोकने को संवर कहते हैं। कर्म को रोकने की 57 विधियाँ हैं। (7) बंध-इससे भाव बंधन है। यह जीव (आत्मा) का पुदगल (परमाणु) से मेल है। बंध के लिए पाँच कारण जिम्मेवार हैं। (8) निर्जर-इस से भाव है दूर भगाना। यह कर्मों को नष्ट करने और जला देने का कार्य करता है। (9) मोक्ष-इसमें जीव कर्मों के जंजाल से मुक्त हो जाता है। यह पूर्ण शाँति की अवस्था है जिसमें हर तरह के दुःखों से छुटकारा प्राप्त हो जाता है।
4. कर्म सिद्धांत (Karma Theory)-जैन दर्शन में कर्म सिद्धांत को एक महत्त्वपूर्ण स्थान प्राप्त है। इस सिद्धांत के अनुसार, “जैसा करोगे वैसा भरोगे, जैसे बीजोगे वैसा काटोगे, यदि कर्म अच्छे होंगे तो अच्छा फल मिलेगा, बुरा करोगे तो बुरा होगा, किसी भी स्थिति में कर्मों से छुटकारा नहीं मिलेगा।” जैसे ही हमारे मन में कोई अच्छा या बुरा विचार आता है वह तुरंत जीव (आत्मा) से उसी तरह जुड़ जाता है, जैसे तेल लगे हुए शरीर में धूलि कण चिपक जाते हैं। ये कर्म आठ प्रकार के हैं-(1) ज्ञानवर्णीय कर्म-यह आत्मा के ज्ञान को रोकते हैं। (2) दर्शनवर्णीय कर्म-यह आत्मा की इच्छा शक्ति को रोकते हैं। (3) वैदनीय कर्म-ये सुख-दुःख उत्पन्न करने वाले कर्म हैं। (4) मोहनीय कर्म-ये आत्मा को मोह माया में फंसाने वाले कर्म हैं। (5) आयु कर्मये कर्म मनुष्य की आय को निर्धारित करते हैं। (6) नाम कर्म-ये कर्म मनुष्य की आय को निर्धारित करते हैं। (7) गोत्र कर्म-ये व्यक्ति के गोत्र और समाज में उसके ऊँचे या नीचे स्थान को निर्धारित करते हैं। (8) अंतरीय कर्म-ये अच्छे कर्म को रोकने वाले कर्म हैं।
कर्मों के कारण मनुष्य आवागमन के चक्रों में फंसा रहता है। कर्मों का नाश करके ही मनुष्य इससे छुटकारा प्राप्त कर सकता है।
5. अनेकांतवाद (The Doctrine of Manyness)-अनेकांतवाद जैन दर्शन का एक अनोखा दार्शनिक सिद्धांत है। अनेकांत शब्द किसी भी पदार्थ के अनेक धर्मों या गुणों का संकेत करता है। इसका भाव यह है कि जिस वस्तु का ज्ञान हमें जिस रूप में होता है, उसी वस्तु का ज्ञान किसी अन्य व्यक्ति को किसी और रूप में हो सकता है। उदाहरणतया जैसे एक बच्चे को उसकी माँ पुत्र समझती है, बहन भाई समझती है, दादी पोता समझती है, नानी दोहता समझती है और बच्चे उसको अपना मित्र समझते हैं। कहने से.भाव यह है कि हर पदार्थ अनेकांत या अनेक गुणों वाला है। इसी कारण हर पदार्थ के बारे में हमारा ज्ञान आंशिक होता है। इसको स्यादवाद कहा जाता है। यह अनेकांतवाद का दूसरा रूप है।
6. पाँच अणुव्रत अथवा महाव्रत (Five Annuvartas or Mahavartas)-जैन धर्म के अनुसार मनुष्य को अपने जीवन में पाँच अणुव्रतों अथवा महाव्रतों की पालना करनी चाहिए। इनके अनुसार (i) मनुष्य को सदा अहिंसा की नीति पर चलना चाहिए। (ii) उसको हमेशा सत्य बोलना चाहिए। (iii) उसको कोई भी ऐसी वस्तु अपने पास नहीं रखनी चाहिए जो उसको दान में प्राप्त न हुई हो। (iv) उसको अपने पास धन नहीं रखना चाहिए। (v) उसको ब्रह्मचर्य का पालन करना चाहिए।
इनमें से पहले चार सिद्धांतों का प्रचलन पार्श्वनाथ ने किया जबकि पाँचवां सिद्धांत महावीर जी ने शामिल किया। डॉक्टर के० सी० सौगानी के अनुसार,
“इन पाँच अणुव्रतों का पालन व्यक्तिगत और सामाजिक उन्नति लाने में सहायक है।’2
7. शुद्ध आचरण (Good Character) स्वामी महावीर ने शुद्ध आचरण को विशेष महत्त्व दिया। उन्होंने कहा कि हमें चोरी, झूठ, चुगली, लालच आदि बुराइयों से दूर रहना चाहिए। उन्होंने कहा कि हमें सादा और पवित्र जीवन व्यतीत करना चाहिए। मनुष्य को पापी से नहीं, बल्कि पाप से नफरत करनी चाहिए।
8. चौबीस तीर्थंकरों की पूजा (Worship of Twenty Four Tirthankaras) जैन धर्म को मानने वाले अपने 24 तीर्थंकरों को देवते मान कर उनकी पूजा करते हैं। उनका विश्वास है कि तीर्थंकरों में पक्का विश्वास रखने से मनुष्य को निर्वाण की प्राप्ति होती है।
9. समानता में विश्वास (Belief in Equality)-जैन धर्म समानता के सिद्धांत में विश्वास रखता है। इसके अनुसार सारे मनुष्य बराबर हैं। इसलिए मनुष्यों को अमीर-गरीब, ऊँच-नीच आदि का भेदभाव नहीं करना चाहिए।
10. यज्ञों, बलियों आदि में अविश्वास (Disbelief in Yajnas and Sacrifices etc.)—जैन धर्म यज्ञों, बलियों और अन्य झूठे रीति-रिवाजों को एक अन्य ढोंग मात्र ही बताता है। उनके अनुसार कोई भी मनुष्य धर्म के बाह्य दिखावे से निर्वाण प्राप्त नहीं कर सकता। इसलिए जैन धर्म के लोगों को इन अंध-विश्वासों से दूर रहने को कहा।
11. वेदों और संस्कृत भाषा में अविश्वास (Disbelief in Vedas and Sanskrit Language)-स्वामी महावीर जी हिंदुओं के पवित्र ग्रंथ-वेदों में कोई विश्वास नहीं रखते थे। उनका कहना था कि वेदों की रचना ईश्वरीय ज्ञान से नहीं हुई। इसलिए वेदों के मंत्रों को पढ़ना बिल्कुल व्यर्थ है। वह संस्कृत भाषा की पवित्रता में भी विश्वास नहीं रखते थे। उन्होंने सारी भाषाओं को पवित्र माना। उन्होंने अपने उपदेशों का प्रचार उस समय में प्रचलित अर्धमगधी भाषा में किया।
12. ईश्वर में अविश्वास (Disbelief in God)-जैन धर्म ईश्वर की उपस्थिति में विश्वास नहीं रखता है। इसके अनुसार ईश्वर संसार की रचना, इसकी पालना और समाप्ति करने वाला नहीं है। निर्वाण प्राप्त करने के लिए ईश्वर की कोई जरूरत नहीं है। मनुष्य की आत्मा ही उसकी महान् शक्ति है। मनुष्य सादा और पवित्र जीवन व्यतीत करके निर्वाण की प्राप्ति कर सकता है।
13. निर्वाण (Nirvana) ‘महावीर जी के अनुसार मनुष्य के जीवन का मुख्य उद्देश्य निर्वाण प्राप्त करना है। जैनमत में निर्वाण से भाव आवागमन के चक्र से मुक्ति प्राप्त करना है। निर्वाण प्राप्ति के बाद मनुष्य का इस संसार में जन्म-मरण का चक्र समाप्त हो जाता है और उसको स्थाई शाँति मिलती है।
1. “Ahimsa is the sheet anchor of Jainism.” B.N. Luniya, Life and Culture in Ancient India (Agra : 1982) p. 162.
2. “The observance of these five vows is capable of bringing about individual as well as social progress.” Dr. K.C. Sogani, Jainism (Patiala : 1986) p. 65.
प्रश्न 5.
भगवान् महावीर का जीवन तथा प्रसिद्ध शिक्षाएँ बताएँ।
(Describe the life and important teachings of Bhagwan Mahavira.)
उत्तर-
जैन धर्म में कुल 24 तीर्थंकर हुए हैं। 24वें तीर्थंकर स्वामी महावीर के जीवन का संक्षिप्त वर्णन निम्नलिखित अनुसार है—
1. महावीर का जन्म और बचपन (Birth and Childhood of Mahavira)- महावीर का जन्म 599 ई० पू० वैशाली (बिहार) के नज़दीक कुंडग्राम में हुआ। कुछ इतिहासकार उनकी जन्म तिथि 540 ई० पू० बताते हैं। महावीर के बचपन का नाम वर्धमान था। महावीर जी के पिता जी का नाम सिद्धार्थ था और वह एक क्षत्रिय कबीले जनत्रिका के मुखिया थे। महावीर जी की माता जी का नाम तृषला था। वह लिच्छवी वंश के शासक चेटक की बहन थी। भगवान् महावीर के जन्म से पूर्व उसे 14 स्वप्न आए थे। महावीर को शिक्षा देने के लिए विशेष प्रबंध किये गये थे। महावीर जी का बचपन से ही सांसारिक वस्तुओं से कोई लगाव नहीं था। वह अपने ही विचारों में डूबे रहते थे।
2. विवाह (Marriage)—सांसारिक कार्यों की ओर महावीर जी का ध्यान लगाने के लिए उनके पिता जी ने महावीर का विवाह एक सुंदर राजकुमारी यशोदा से कर दिया। विवाह के समय महावीर जी की आयु कितनी थी इसके बारे हमें कोई निश्चित जानकारी प्राप्त नहीं है। कुछ समय पश्चात् महावीर जी के घर एक पुत्री ने जन्म लिया। उसका नाम प्रियादर्शना रखा गया।
3. महान् त्याग और ज्ञान प्राप्ति (Renunciation and Enlightenment)-गृहस्थी जीवन भी महावीर जी की धार्मिक रुचियों की राह में किसी तरह की अड़चन (रुकावट) न बन सका। अपने माता-पिता की मृत्यु हो जाने के बाद महावीर अपने बड़े भाई नंदीवर्मन से आज्ञा लेकर गृह त्याग्न कर जंगलों में ज्ञान की खोज के लिए चले गये। उस समय महावीर जी की आयु 30 वर्ष थी। उन्होंने 12 वर्षों तक बड़ा कठोर तप किया। अंततः उनको ऋजुपालिका नदी के नज़दीक जरिमबिक गाँव में कैवल्य ज्ञान (सर्वोच्च सत्य) प्राप्त हुआ। इस ज्ञान की प्राप्ति के बाद वर्धमान जिन (इंद्रियों पर जीत प्राप्त करने वाला) और महावीर (महान् विजयी) कहलाये। ज्ञान प्राप्ति के समय महावीर जी की आयु 42 वर्ष थी।
4. धर्म प्रचार (Preachings)-ज्ञान प्राप्ति के बाद महावीर जी ने लोगों में फैले अंधविश्वासों को दूंर करने के लिए और उनको सच्चा मार्ग बताने के लिए अपने उपदेशों का प्रचार किया। उनके उपदेशों से बहुत सारे लोग प्रभावित हुए और वे महावीर जी के अनुयायी बन गये। महावीर जी के प्रसिद्ध प्रचार केंद्र राजगृह, वैशाली, कौशल, मिथिला, विदेह और अंग थे। जैन परंपराओं के अनुसार मगध के शासक बिंबिसार और उसके पुत्र अजातशत्रु ने जैन मत को स्वीकार कर लिया।
5. निर्वाण (Nirvana)—स्वामी महावीर ने लगभग 30 वर्षों तक अपना प्रचार किया। 72 वर्ष की आयु में पावा (पटना) में 527 ई० पू० में उन्होंने निर्वाण (मुक्ति) प्राप्त किया। उस समय महावीर जी के 14,000 अनुयायी थे।

प्रश्न 6.
जैन धर्म में त्रि-रत्न से क्या अभिप्राय है ? चर्चा करें।
(What is meant by three Jewels in Jainism ? Discuss.)
अथवा
‘त्रि-रत्न’ की व्याख्या करो और बताओ कि यह किस धर्म से संबंधित है ? (Explain Tri-Ratna and tell to which religion, do they belong.)
अथवा
जैन मत के तीन हीरों की व्याख्या करें।
(Explain the three Jewels of Jainism.).
अथवा
जैन धर्म के त्रि-रत्नों के बारे में चर्चा करो।
(Discuss the Tri-Ratnas of Jainism.)
उत्तर-
जैन दर्शन के सिद्धांतों से यह बात स्पष्ट हो जाती है कि पहले जीव (आत्मा) शुद्ध रूप में होता है। बाद में यह कार्मिक पदार्थों के कारण दूषित हो जाता है। इसके परिणामस्वरूप व्यक्ति को घोर दुःखों का सामना करना पड़ता है। यदि कार्मिक पदार्थों का नाश कर दिया जाये तो व्यक्ति इस भवसागर से पार उतर सकता है और मोक्ष प्राप्त कर सकता है। जैन दर्शन मोक्ष प्राप्ति को मनुष्य के जीवन का सबसे ऊँचा उद्देश्य मानता है। कोई भी व्यक्ति बिना किसी जाति, लिंग, धर्म, वर्ग या आयु पर इस मार्ग पर चल सकता है। इस मार्ग पर चलने के लिए जैन धर्म में त्रि-रत्न निर्धारित किये गये हैं। ये त्रि-रत्न हैं-(1) सच्चा विश्वास (2) सच्चा ज्ञान (3) सच्चा आचार। ये त्रि-रत्न मोक्ष प्राप्ति के तीन भिन्न-भिन्न मार्ग नहीं हैं, बल्कि एक मार्ग के तीन साथ-साथ चलने वाले रास्ते हैं। यदि इनमें से एक की भी कमी हो तो व्यक्ति अपने उद्देश्य की प्राप्ति नहीं कर सकता। उदाहरण के तौर पर यदि किसी व्यक्ति ने अपने मकान की छत पर जाना हो तो उसको सीढ़ी लगानी पड़ेगी और यदि इस सीढ़ी के सिरे पर लगे दो और बीच में लगे डंडों में से एक चीज़ की भी कमी हो तो व्यक्ति किसी भी स्थिति में ऊपर नहीं पहुँच सकता। त्रि-रत्नों का संक्षेप वर्णन निम्नलिखित है—
1. सच्चा विश्वास (Right Belief)-जैन दर्शन के त्रि-रत्नों में सच्चा विश्वास नामक रत्न को पहला अथवा प्रमुख स्थान दिया गया है। क्योंकि यदि व्यक्ति में सच्चा विश्वास न हो तो वह सच्चा ज्ञान और सच्चा आचार कभी प्राप्त नहीं कर सकता। सच्चा विश्वास से भाव यह है कि जो व्यक्ति मोक्ष प्राप्त करना चाहता है, उसे 24 जैन तीर्थंकरों, नौ महान् सच्चाइयों और जैन शास्त्रों में पक्की श्रद्धा होनी चाहिए। जैन शास्त्रों के अनुसार सच्चा विश्वास तभी पूरा हो सकता है यदि संबंधित व्यक्ति 8 अंगों को धारण करे। ये 8 अंग हैं—
- जैन धर्म के सिद्धांतों के बारे कोई शंका नहीं होनी चाहिए।
- सांसारिक वस्तुओं से कोई प्यार नहीं होना चाहिए।
- शरीर में चाहे अनगिनत बुराइयाँ हैं, परंतु इसके प्रति कोई तिरस्कार की भावना नहीं होनी चाहिए।
- गलत मार्ग की ओर कोई झुकाव नहीं होना चाहिए।
- पवित्र व्यक्तियों की प्रशंसा की जानी चाहिए, परंतु दूसरे व्यक्तियों की निंदा नहीं की जानी चाहिए।
- जो व्यक्ति धर्म की राह से भटक गये हों उनको ठीक मार्ग दर्शाना चाहिए।
- धार्मिक व्यक्तियों का पूरा आदर किया जाना चाहिए।
- जैन सिद्धांतों के प्रचार के लिए पूरे यत्न करने चाहिए।
सच्चा विश्वास किसी भी व्यक्ति द्वारा तब ही प्राप्त किया जा सकता है यदि वह तीन प्रकार के अंध-विश्वासों और आठ प्रकार के घमंडों से दूर रहे। तीन तरह के अंध-विश्वास ये हैं—
- पहाड़ पर चढ़कर, नदी में नहाकर या आग पर चल कर अपने आप को पवित्र समझना।
- झूठे देवी-देवताओं में विश्वास करना।
- झूठे तपस्वियों का सत्कार करना।
आठ प्रकार के घमंड ये हैं—
- ज्ञान का घमंड
- पूजा का घमंड
- परिवार का घमंड
- जाति का घमंड
- शक्ति का घमंड
- दौलत का घमंड
- तप का घमंड
- सुंदर शरीर का घमंड।
सच्चा विश्वास हमारे लिए समृद्धि तथा मोक्ष का आधार तैयार करता है।
2. सच्चा ज्ञान (Right Knowledge)-सच्चा विश्वास ही सच्चे ज्ञान की आधारशिला है। इस कारण सच्चा विश्वास और सच्चे ज्ञान के मध्य गहरा संबंध है। सच्चा ज्ञान वह है जो जैन शास्त्रों में दिया गया है। जो व्यक्ति मोक्ष प्राप्त करना चाहता है उसके लिए सच्चे ज्ञान को प्राप्त करना अति ज़रूरी है। यह ज्ञान बाहर से नहीं आता बल्कि जीव पर पड़े कर्म पदार्थों के पर्दे को दूर हटाने से उत्पन्न हो जाता है। इस ज्ञान के दो रूप बताये गये हैं जिनको प्रत्यक्ष ज्ञान और परोक्ष ज्ञान कहा जाता है। वह ज्ञान जो आत्मा द्वारा सीधा प्राप्त किया जाता है प्रत्यक्ष ज्ञान कहलाता है और वह ज्ञान जो इंद्रियों के रास्ते से प्राप्त होता है परोक्ष ज्ञान कहलाता है।
जैनी ज्ञान को पाँच तरह का बताते हैं—
- मति ज्ञान-यह ज्ञान इंद्रियों द्वारा प्राप्त किया जाता है और यह सीमित होता है।
- श्रुती ज्ञान-यह ज्ञान शास्त्रों को पढ़ने और या सुनने से प्राप्त होता है। इससे भूत, वर्तमान और भविष्य संबंधी ज्ञान प्राप्त किया जा सकता है। यह ज्ञान भी इंद्रियों के द्वारा जाना जा सकता है।
- अवधि ज्ञान-दूर के समय या स्थान के बारे जो ज्ञान आत्मा के द्वारा होता है उसको अवधि ज्ञान कहते हैं।
- मनपर्याय ज्ञान-यह वह ज्ञान है जिस द्वारा व्यक्ति किसी दूसरे के मन के विचारों को जान सकता है। यह ज्ञान भी आत्मा द्वारा होता है।
- कैवल्य ज्ञान-यह पूर्ण सच्चा ज्ञान है। इसको परमार्थिक ज्ञान भी कहा जाता है। इस ज्ञान को प्राप्त करने वाले व्यक्ति को सिद्ध कहा जाता है।
ज्ञान दोष तीन तरह से पैदा होता है—
- इंद्रियों की गलती के कारण।
- गलत अध्ययन के कारण।
- अस्पष्ट दृष्टिकोण के कारण।
जैसे दूध की भारी मात्रा में थोड़ा-सा खट्टा डाल दिया जाये तो वह सारे दूध को खट्टा कर देता है। ठीक उसी तरह यदि व्यक्ति द्वारा प्राप्त ज्ञान में थोड़ा-सा भी दोष आ जाये तो वह सच्चा ज्ञान प्राप्त नहीं कर सकता।
3. सच्चा आचार (Right Conduct)-मोक्ष को प्राप्त करने के लिए व्यक्ति के लिए सच्चा विश्वास और सच्चा ज्ञान होने के बाद सच्चा आचार का होना अति ज़रूरी है। व्यक्ति का सच्चा आचार ही जीव के कार्मिक पदार्थों का नाश करता है और उसके लिए मोक्ष का मार्ग तैयार करता है। सच्चे आचार पर चलने के लिए जैन धर्म में कुछ नियम निर्धारित किये गये हैं। ये नियम यद्यपि समान रूप में आम लोगों और जैन मुनियों पर लागू होते हैं परंतु उन पर सख्ती का अंतर है । जैन मुनियों को इन नियमों की सख्ती से पालना करनी पड़ती है जबकि आम लोगों को कुछ छूट दी गई है। इन नियमों को पाँच महाव्रत या पाँच अणुव्रत कहा जाता है इनके अनुसार—
- मनुष्य को कभी किसी जीव को दु:ख नहीं देना चाहिए और उसको अहिंसा की नीति पर चलना चाहिए।
- उसको सदा सत्य बोलना चाहिए। उसके बोल मीठे और हितकारी होने चाहिए।
- उसको कोई भी ऐसी वस्तु अपने पास नहीं रखनी चाहिए जो उसको दान में प्राप्त न हुई हो।
- उसको सांसारिक वस्तुओं से मोह नहीं करना चाहिए।
- उसको ब्रह्मचर्य का पालन करना चाहिए।
ऊपरलिखित त्रि-रत्नों पर चलने के कारण जीव के कर्म पदार्थ धीरे-धीरे नष्ट होने शुरू हो जाते हैं और वह अपने परम उद्देश्य मोक्ष को प्राप्त करता है। अंत में हम प्रसिद्ध लेखक जे० पी० सुधा के इन शब्दों से सहमत हैं,
“जैनियों के अनुसार सच्चा विश्वास, सच्चा ज्ञान और सच्चा आचार जो त्रि-रत्नों के तौर पर जाने जाते हैं उस मार्ग का निर्धारण करते हैं जो जीव अपने अंदर कार्मिक पदार्थों को आने से रोकते हैं और व्यक्ति को आवागमन के बंधनों से मुक्त करते हैं।”3
3. “According to the three jewels of right faith, right knowledge and right conduct, known as Triratna constitute the path which prevents fresh Karmic matter from entering the soul and frees the individual from the bonds of rebirth.” J.P. Sudha, Religions in India (New Delhi : 1978) p. 211.
प्रश्न 7.
जैन धर्म में अहिंसा पर नोट लिखें। (Write a note on Ahimsa (non-violence) of Jainism.)
अथवा
जैन धर्म में अहिंसा के सिद्धांत के बारे में प्रकाश डालें।
(Throw light on the Jain principle of Ahimsa.)
अथवा
अहिंसा से क्या भाव है ? जैन धर्म में इसका क्या महत्त्व है ? (What is meant by Ahimsa ? What is its importance in Jainism ?)
अथवा
जैन धर्म में अहिंसा के सिद्धांत पर नोट लिखें।
(Write a note on the concept of Ahimsa in Jainism.)
उत्तर-
1. अहिंसा से अभिप्राय (Meaning of Ahimsa)-जैन धर्म में अहिंसा की नीति को जितना महत्त्व दिया गया है उतना विश्व के किसी अन्य धर्म में नहीं दिया गया। यदि अहिंसा को जैन धर्म की आधारशिला कह दिया तो इसमें कोई अतिकथनी नहीं होगी। अहिंसा से अभिप्राय है किसी भी जीवित चीज़ को कोई कष्ट न देना। जीवित जीवों को कस के बाँधने, उनको मारने-पीटने, उनकी हिम्मत से अधिक भार जोतने, उनको खुराक और पानी से वंचित रखने में जैन धर्म में मनाही है। इनके अतिरिक्त उनको अपने भोजन के लिए मारना बिल्कुल अनुचित है।
जैन दर्शन के अनुसार वृक्षों और पत्थरों आदि में भी जान होती है। इसलिए हमें उनको भी किसी किस्म का दु:ख नहीं देना चाहिए। आचारांग सूत्र में कहा गया है, “सभी को अपना जीवन प्यारा है, सभी सुख चाहते हैं, दुःख कोई नहीं चाहता, अधिक कोई नहीं चाहता, सब को जीवन प्यारा है और सभी जीने की इच्छा रखते हैं।” इसलिए जो हमारे लिए सुखमयी है वह दूसरों के लिए भी सुखमयी है।
2. दो प्रकार की हिंसा (Two types of Ahimsa)-हिंसा दो प्रकार की होती है-विचार या मन से हिंसा और कर्म से भाव शारीरिक और बाहरी हिंसा। बाहरी हिंसा के व्यवहार में आने से पहले मनुष्य के विचारों में हिंसा आती है। जब मनुष्य के मन में आवेग उठते हैं और इन आवेगों के प्रति विचार उत्पन्न होते हैं तो व्यक्ति पाप करता है और हिंसा का दोषी बन जाता है। मनुष्य संसार के लालचों में फंसकर अपनी काम वासना को पूरा करने के लिए , किसी को धोखा देने के लिए, किसी से अपना बदला लेने के लिए हिंसा करता है। जब इससे संबंधित विचार व्यक्ति के मन में आते हैं तो वह पहले अपनी आत्मा को दूषित करता है। वह यहाँ ही बस नहीं करता और बाद में बाहरी हिंसा के द्वारा दूसरों को दुःख पहुँचाता है और स्वयं भी दुःखी होता है। हिंसा को रोकने के लिए व्यक्ति का अपने विचारों को शुद्ध करना ज़रूरी है। महावीर ने अपने शिष्यों को शिक्षा देते हुए कहा, “हे श्रमणो, पहले अपने आप से युद्ध करो और आत्म शुद्धि की ओर कदम बढ़ाओ। बाहरी युद्ध से कुछ नहीं होगा।”
3. अहिंसा जीवन का एक मार्ग (Ahimsa is a way of Life)-जैन दर्शन में अहिंसा को जीवन का एक मार्ग कहा गया है। किसी भी व्यक्ति द्वारा अहिंसा के प्रति प्रतिज्ञा का पूरी तरह पालन तभी संभव है यदि उसको हिंसा की किस्मों और रूपों के बारे में पूर्ण ज्ञान हो। जैनी सूत्रों में 108 प्रकार की हिंसा का वर्णन मिलता है जिन्हें चार वर्गों में बाँटा जा सकता है। पहले वर्ग में हिंसा तीन स्तर की है। हिंसा व्यक्ति स्वयं कर सकता है, यह दूसरों से करवाई जा सकती है और यह उसकी अपनी सहमति के द्वारा की जा सकती है। व्यक्ति मन, वाणी और शरीर द्वारा हिंसा कर सकता है। दूसरे वर्ग में तीन स्तरीय हिंसा नौ स्तरीय बन जाती है क्योंकि यह मन, वाणी और शरीर रूपी तीन साधनों में प्रत्येक साधन द्वारा की जा सकती है। तीसरे वर्ग में नौ स्तरीय हिंसा सताईस स्तरीय बन जाती है क्योंकि हिंसा की तीन स्थितियाँ हैं, भाव हिंसा के बारे में सोचना, हिंसा के लिए तैयारी करना और फिर उस को व्यावहारिक रूप देना। चौथे वर्ग में सत्ताईस स्तरीय हिंसा 108 स्तरीय हिंसा बन जाती है क्योंकि यह चार मनोवेगों में से किसी न किसी से उत्तेजित होती है।
4. हिंसा से बचने के साधन (Ways to Escape Ahimsa)-हिंसा के सभी रूपों में किसी से बचना आसान नहीं है। फिर भी जैनी अपने जीवन में इनसे बचने के लिए अनेक नियमों का पालन करते हैं। वे नंगे पाँव चलते हैं ताकि कोई कीड़ा उनके पाँवों के नीचे आकर मर न जाये। वे मुँह पर पट्टी बाँध कर रखते हैं ताकि कोई कीटपतंगा सांस से उनके अंदर न चला जाए। इस उद्देश्य से वे पानी छान कर पीते हैं और सूर्य ढलने के बाद भोजन नहीं करते। जैनी ज्यादातर व्यापार का धंधा करते हैं और खेतीबाड़ी बिल्कुल नहीं करते क्योंकि उनका विचार है कि खेतीबाड़ी करते समय अनेक जीवों की हत्या हो जाती है।
जैन धर्म में व्यक्ति के मन में हिंसा के विचारों को उभरने से रोकने के लिए शराब और दूसरी नशीली वस्तुओं के सेवन, माँस खाने और युद्ध करने की मनाही है। नशीली वस्तुओं का प्रयोग करने से हमारे अंदर काम वासना और अन्य कई वासनाएँ उत्तेजित होती हैं। इनसे पाप की भावना और हिंसा उत्पन्न होती है। परिणामस्वरूप व्यक्ति लापरवाही में ही हिंसा कर देता है। माँस का प्रयोग करने पर इसलिए पाबंदी लगाई गई है ताकि मनुष्य पशुओं और पक्षियों को अपने भोजन के लिए न मारे और न ही वह हिंसा का भागीदार बने। युद्ध के दौरान व्यक्ति अपने दुश्मनों को मार कर बहुत बहादुरी का काम समझता है परंतु जैन दर्शन के अनुसार किसी भी व्यक्ति को मारना बिल्कुल अयोग्य है।

ऊपरलिखित विवरण से स्पष्ट है कि जैन धर्म में अन्य नियमों के मुकाबले अहिंसा के सिद्धांत पर अधिक बल दिया गया है। डॉक्टर ज्योति प्रसाद जैन का यह कहना बिल्कुल ठीक है,
“अहिंसा का जीवन सारी नैतिक, सामाजिक, आर्थिक और राजनीतिक बुराइयों का राम बाण इलाज है। अहिंसा सर्वोच्च धर्म है और जहाँ अहिंसा है वहाँ जीत है।”4
4. “The Ahimstic way of life is the sure panacea for all moral, social, economic and political ills. Ahimsa is the highest religion, and where there is Ahimsa, there is victory.” Dr. Jyoti Prasad Jain, Religion and Culture of the Jains (New Delhi : 1983) p. 101.
प्रश्न 8.
जैन धर्म की नौ सच्चाइयों से क्या भाव है ? इनका संक्षेप वर्णन करो। (What is meant by Nine Truths of Jainism ? Explain briefly.)
अथवा
जैन धर्म के नौ तत्त्व कौन से हैं ? चर्चा करें।
(Which are the nine tatvas in Jainism ? Discuss.)
अथवा
जैन धर्म के नौ तथ्यों पर एक नोट लिखो।
(Write a note on nine tatvas of Jainism.)
अथवा
जैन धर्म के नौ तत्त्वों से हमें क्या शिक्षा मिलती है ?
(What do we learn from nine tatvas of Jainism ?)
अथवा
जैन धर्म के नौ रत्नों के बारे में जानकारी दीजिए।
(Describe the Nine Rattans of Jainism.)
उत्तर-
नौ सच्चाइयों अथवा तत्त्वों को जैन दर्शन में केंद्रीय स्थान प्राप्त है। वह व्यक्ति जो निर्वाण प्राप्त करने का चाहवान है उसके लिए इन नौ सच्चाइयों के बारे जानकारी होना अति जरूरी है। ये नौ सच्चाइयाँ हैं—
(i) जीव
(ii) अजीव
(iii) पुण्य ”
(iv) पाप
(v) आश्रव
(vi) बंध
(vii) संवर
(viii) निर्जर
(ix) मोक्ष।
दिगंबर संप्रदाय के अनुसार सात सच्चाइयाँ हैं । वे पाप और पुण्य को अलग नहीं मानते। उनके अनुसार ये अश्रव और बंध में शामिल हैं। इन सच्चाइयों का संक्षेप वर्णन निम्नलिखित अनुसार है—
1. जीव (Jiva)-जीव शब्द का अर्थ है आत्मा। यह चेतन तथ्य है। जैन दर्शन में जीव दो प्रकार के हैं। इनको सांसारिक जीव और मुक्त जीव कहा जाता है। सांसारिक जीव को बंधन जीव भी कहते हैं। यह जीव आवागमन के चक्र में रहता है और अपने कर्मों के अनुसार बार-बार जन्म लेता है और अपने अच्छे बुरे फल भुगतता है। मुक्त जीव वह जीव है जो पुनर्जन्म से रहित है। यह जीव अनंत ज्ञान वाला, अनंत शक्ति वाला और अनंत गुणों वाला होता है। यह जीव कर्मों के जाल से मुक्त होता है।
2. अजीव (Ajiva)-अजीव से भाव उन जड़ पदार्थों से है जिनमें चेतना नहीं होती जैसे पुस्तक, कागज़, मेज़ और स्याही आदि। उदाहरण के तौर पर ऊँट के शरीर में जीव फैल कर ऊँट जितना बड़ा हो जाता है और कीड़ी के शरीर में सिकुड़ कर कीड़ी जितना हो जाता है। यह जीव तब नहीं दिखाई देता है परंतु शरीर की क्रियाओं के आधार पर इसकी उपस्थिति का ज्ञान हो जाता है। परंतु जब शरीर का अंत हो जाता है तो जीव लोप हो जाता है। जीव जिस शरीर को धारण करता है वह उस के आकार का ही हो जाता है। अजीव दो प्रकार के होते हैं रूपी और अरूपी । रूपी वह हैं जो दिखाई देते हैं जैसे कुर्सी, पैन, घड़ा आदि। अरूपी वह हैं जो दिखाई नहीं देते जैसे समय, चिंता और खुशी आदि। जैन दर्शन में अजीवों के पाँच अचेतन तत्त्व बताए गए हैं। इनका संक्षेप वर्णन निम्नलिखित है
- पुदगल (Pudgala)-पुदगल से भाव पदार्थ या परमाणु है। यह पुदगल रूप, स्पर्श, रस और गंध-चार गुणों वाले होते हैं। अग्नि के पुदगल रूप गुण वाले, वायु के पुदगल स्पर्श गुण वाले, जल के पुदगल रस गुण वाले और पृथ्वी के पुदगल गंध गुण वाले होते हैं। पुदगलों के दो रूप माने गए हैं-अणु रूप वाले और स्कंध रूप वाले। अणु रूप वाले पुदगल जीवों के भोग के लायक नहीं होते हैं जबकि स्कंध रूप वाले होते हैं। पुदगलों को सारे भौतिक जगत् की रचना का मूल आधार माना जाता है।
- धर्म (Dharma) यह तत्त्व जीव और पुदगलों में गति पैदा करता है और उनके आपसी सहयोग में सहायक माना जाता है। जैसे मछली की गति के लिए पानी की ज़रूरत अति आवश्यक है ठीक उसी प्रकार जीवों और पुदगलों की गति के लिए धर्म की ज़रूरत अति आवश्यक है। धर्म के बिना गति पैदा नहीं हो सकती।
- अधर्म (Adharma)-इसका स्वरूप और कार्य धर्म से बिल्कुल उल्ट है। यह जीवों की ओर पुदगलों की गति में रुकावट पैदा करता है। परंतु अधर्म को धर्म का विरोधी नहीं समझा जाता। अधर्म के द्वारा गति में पाई गई रुकावट जीव के आराम के लिए सहायक मानी गई है।
- आकाश (Akasha)-आकाश से भाव वह स्थान है जिसमें जीव, मुदगल, धर्म और अधर्म सारे विस्तार वाले तत्त्व रहते हैं। इन तत्त्वों के आधार पर ही आकाश की उपस्थिति का अनुमान किया जाता है। जैन दर्शन के अनुसार आकाश दो प्रकार के हैं-लोकाकाश और अलोकाकाश। लोकाकाश उस आकाश को कहा गया है जिस भाग में भौतिक लोक की स्थिति है और उससे ऊपर जो आकाश है उसको अलोकाकाश कहा गया है।
- काल (Kala)-काल से भाव समय है। यह विस्तार वाला तत्त्व नहीं है। इसकी उपस्थिति का ज्ञान अनुमान के द्वारा प्राप्त होता है। काल को जगत् के परिवर्तन का मूल कारण माना गया है। भूत, वर्तमान, भविष्य से काल का संबंध है। काल को आदि और अंत वाला तत्त्व कहा जाता है।
3. पुण्य (Punya)-पुण्य वह कर्म है जो अच्छे अमलों से कमाये जाते हैं। पुण्य कमाने के अलग-अलग ढंग हैं। भूखे को खाना देना, प्यासे को पानी पिलाना, नंगे को कपड़ा देना, हाथों से सेवा करनी, मीठा बोलना आदि पुण्य के काम हैं, पुण्य को मानने के 42 साधन हैं। अच्छी सेहत, आर्थिक समृद्धि, प्रसिद्धि, अच्छा वैवाहिक जीवन, अच्छे रिश्तेदारों और दोस्तों का मिलना, अच्छी पढ़ाई और उच्च पदवियों पर नियुक्ति आदि अच्छे पुण्यों का ही नतीजा है। पुण्य को आत्मा का सहायक माना जाता है क्योंकि इससे खुशी प्राप्त होती है।
4. पाप (Papa)-पाप को जीव के बंधन का मुख्य कारण माना जाता है। जीवों को मारना, झूठ, चोरी, क्रोध, लोभ, मोह, अहंकार, धोखा, नशा और दुश्मनी आदि सब पापों के भार में वृद्धि करते हैं। पापियों को घोर सजाएँ . मिलती हैं। आपने देखा होगा कि एक ही घर में पैदा हुए दो सगे भाइयों के जीवन में भारी अंतर होता है। एक ऊँची पदवी पर सुशोभित होता है और उसको प्रसिद्धि प्राप्त होती है। दूसरा दर-दर की ठोकरें खाता फिरता है, चोरियाँ करता है और बदनामी कमाता है। ऐसा क्यों होता है ? जैन दर्शन के अनुसार ऐसा व्यक्ति के पुण्य और पाप कमाने का कारण होता है। पापी मनुष्य कभी भी सुखी नहीं हो सकता और उसको अपने जीवन में घोर संकट का सामना करना पड़ता है। ऐसे व्यक्ति की आत्मा भी तड़पती रहती है। जैन सूत्रों के अनुसार पापों के 82 अलग-अलग परिणाम निकलते हैं।
5. आशरव (Asrava) ब्रह्मांड में अनगिनत सूक्ष्म अणु (कार्मिक पदार्थ) घूमते रहते हैं जिनको आत्मा अपने अच्छे बुरे कर्मों के अनुसार अपनी ओर खींचती है। इस अंदर आने की कारवाई को आश्व कहते हैं। मनुष्य के कर्म आत्मा में उसी तरह शामिल होते हैं जैसे एक सुराख के रास्ते से नाव में पानी। कर्म जीव के बंधन का एक मुख्य कारण है। कर्म जड़ हैं। इसलिए आप जीव में प्रवेश नहीं करते, वे मन, वचन और शरीर की सहायता से जीव में प्रवेश करते हैं। कर्म दो प्रकार के हैं शुभ और अशुभ। यदि शुभ कर्म जीव में प्रवेश होंगे तो उसको सुख की प्राप्ति होगी और यदि कर्म अशुभ होंगे तो जीव को कष्ट होगा। इसलिए कर्मों का शुभ अथवा अशुभ होना व्यक्ति की प्रवृत्ति पर निर्भर करता है।
6. बंध (Bandha)-जब कर्म पदार्थ का पर्दा जीव के शुद्ध स्वरूप पर पड़ जाता है तो वह दूषित हो जाता है। यह जीव के बंधन का कारण बनता है। जैन दर्शन के अनुसार इस दिशा की ओर ले जाने वाले पाँच कारण हैं।
- मिथ्या दर्शन-इससे भाव गलत विश्वास है।
- आवृत्ति-इससे भाव है प्रतिज्ञा की कमी।
- प्रसाद-इससे भाव है लापरवाही।
- काश्य-इससे भाव है काम वासना।
- योग-इससे भाव है शरीर, मन और बोल की प्रक्रिया।
बंध चार प्रकार के हैं—
- प्रकृति-जीव से जुड़े कर्म पदार्थों का स्वरूप।
- स्थिति-कर्म पदार्थ जीव से कितने समय के लिए जुड़े हैं।
- अनुभाग-कर्म पदार्थ सख्त चरित्र के हैं या नर्म चरित्र के। (घ) प्रदेश जीव-जीव से जुड़े कर्म पदार्थों में अणुओं की संख्या।
कर्मों के जाल में फंस कर जीव का व्यावहारिक रूप नष्ट हो जाता है और वह बंधन में फंस जाता है। इस कारण वह बार-बार जन्म लेता है और शरीर रूपी कैद भोगता है।
7. संवर (Sanvara)—योग क्रिया के द्वारा कर्म पदार्थ जीव की ओर खींचे आते हैं। मोक्ष प्राप्त करने के लिए इस क्रिया को रोकना अति ज़रूरी है। इसको संवर कहते हैं। इसको आश्व निरोध भी कहते हैं, जिससे भाव है कर्मों का हमारे अंदर प्रवेश करने से रुक जाना। कर्म को रोकने की 57 विधियाँ हैं। इनमें आत्म संयम, शुभ विचार, लोभ, मोह, अहंकार, क्रोध और पापों से परहेज़ आदि शामिल हैं। इस कारण जीव के इर्द-गिर्द एक ऐसी ऊँची दीवार बन जाती है जिसके अंदर कर्म पदार्थों का दाखिल होना असंभव है। जैसे एक तालाब में जिस नाली के द्वारा पानी जा रहा है उसको रोकना संभव है ठीक उसी प्रकार कर्म पदार्थों को संवर के द्वारा जीव में प्रवेश करने से रोकना संभव है।
8. निर्जर (Nirjara)-निर्जर से भाव कर्म पदार्थों को जीव से दूर हटाना है। यह जीव के द्वारा संचित कर्मों को नष्ट करने का एक मुख्य साधन है। संवर द्वारा जीव में कर्मों के बढ़ने और प्रवेश को रोका जाता है। परंतु पुराने कर्मों को जिन का जीव के भीतर आश्व हो गया है निर्जर के द्वारा नाश किया जा सकता है। निर्जर में तपस्या शामिल है। तपस्या अग्नि की तरह कर्म पदार्थों के इकट्ठे हुए ढेर को जला कर राख कर देती है। इसी प्रकार जब जीव पर से कर्म पदार्थों का पड़ा पर्दा हट जाता है तो उसका शुद्ध स्वरूप प्रकट हो जाता है। जैसे बिलौर के सामने काला कपड़ा रखने से वह काला नज़र आने लग जाता है। परंतु जब कपड़ा हटा लिया जाता है तो उसकी अपनी चमक दुबारा प्रकट हो जाती है।
9. मोक्ष (Moksha)-जैन दर्शन के अनुसार मनुष्य के जीवन का परम उद्देश्य मोक्ष अथवा निर्वाण को प्राप्त करना है। इसमें जीव कर्मों के सारे बंधनों से मुक्त हो जाता है। कर्मों की समाप्ति से मनुष्य मोक्ष प्राप्त करता है। इसलिए संवर और निर्जर आवश्यक है। कर्मों के बंधन को तोड़ने के लिए जैनी तीन सद्गुणों के पालन की सिफ़ारिश करते हैं, जिनको त्रि-रत्न कहा जाता है। ये हैं सच्चा विश्वास, सच्चा ज्ञान और सच्चा आचार। मोक्ष जीव की प्राप्ति की सर्वोच्च अवस्था है। जो व्यक्ति मोक्ष प्राप्त कर लेता है उसको सिद्ध कहते हैं । सिद्ध पुरुष जन्म, मृत्यु, सुख और दुःख से दूर है। वह ब्रह्मांड में चिरंजीवी शाँति प्राप्त करते हैं।
प्रश्न 9.
जैन धर्म के पाँच महाव्रतों के महत्त्व का उल्लेख करें। (Describe the importance of Five Mahavartas in Jainism.)
अथवा
जैन धर्म के पाँच महाव्रतों के बारे में चर्चा कीजिए।
(Discuss the Five Mahavartas of Jainism.)
अथवा
जैन धर्म में पाँच महाव्रतों का क्या महत्त्व है ? प्रकाश डालिए।
(What is the importance of Five Mahavartas in Jainism ? Elucidate.)
अथवा
जैन धर्म के पाँच अणुव्रतों के बारे में जानकारी दें।
(Describe the Five Anuvartas of Jainism.)
अथवा
जैन धर्म के पाँच अणुव्रतों का क्या महत्व है ? प्रकाश डालें।
(What is the importance of Five Anuvartas of Jainism ? Elucidate.) ।
उत्तर-
जैन धर्म में पाँच महाव्रतों को विशेष स्थान प्राप्त है। इन नियमों की पालना करनी प्रत्येक जैनी के लिए आवश्यक है। ये नियम बहुत कठोर हैं। ये नियम जैन भिक्षुओं और भिक्षुणियों के लिए बनाए गए थे। गृहस्थियों के लिए ये नियम इतने कठोर नहीं थे। इनके लिए बनाए गए नियमों को पाँच अणुव्रत (Five Anuvartas) कहा जाता है। इन पाँच महाव्रतों या अणुव्रतों का संक्षिप्त वर्णन निम्नलिखित अनुसार है—
1. अहिंसा (Ahimsa)-जैन धर्म में अहिंसा पर बहुत ज़ोर दिया गया है। अहिंसा की महत्ता बताते हुए आचारांग सूत्र में कहा गया है, “सभी को अपना-अपना जीवन प्यारा है सब ही सुख चाहते हैं, दुःख कोई नहीं चाहता, अधिक कोई नहीं चाहता, सब को जीवन प्यारा है और सारे ही जीने की इच्छा रखते हैं।” इसीलिए जो हमारे लिए सुखमयी है वह दूसरों के लिए भी सुखमयी है। हिंसा दो तरह की होती है-मन से हिंसा और कर्म से हिंसा। कर्म अथवा अमल में आने वाली हिंसा से पहले मन भाव विचारों में हिंसा आती है। गुस्सा, अहंकार, लालच और धोखा मन की हिंसा है। इसलिए हिंसा से बचने के लिए मन के विचारों को शुद्ध करना अति ज़रूरी है। जैन धर्म के अनुसार मनुष्यों के अतिरिक्त पशुओं, पत्थरों और वृक्षों आदि में भी आत्मा निवास करती है। इसलिए हमें किसी जीव या निर्जीव को कष्ट नहीं देना चाहिए। इसी कारण जैन लोग नंगे पाँव चलते हैं, मुँह पर पट्टी बाँधते हैं, पानी छान कर पीते हैं और अंधेरा हो जाने के बाद कुछ नहीं खाते ताकि किसी जीव की हत्या न हो जाये। बी० एन० लूनीया के अनुसार,
“अहिंसा जैन धर्म की आधारशिला है।”5
2. सत्य (Satya)-जैन धर्म में सत्य बोलने पर बहुत बल दिया गया है। हमें हमेशा सत्य और मीठे वचन बोलने चाहिए। ऐसा करने से व्यक्ति दूसरे के मन को मोह लेता है। झूठ बोलने से आत्मा को दुःख होता है। झूठ बोलने वाला व्यक्ति कभी सुखी नहीं हो सकता। वास्तव में झूठ बोलने से कलह-क्लेश बढ़ता है और इसका अंत नहीं होता। विवश होकर अंत में व्यक्ति को सत्य मानना ही पड़ता है। झूठ के परिणाम हमेशा बुरे ही होते हैं। हमें किसी के डर के कारण, लालच के कारण अथवा हंसी-मज़ाक में भी झूठ नहीं बोलना चाहिए। इसलिए हमें हमेशा सोच-समझ कर बोलना चाहिए। गुस्सा आने पर शांत बने रहना चाहिए। जैन धर्म में इस बात पर भी बल दिया गया है कि हमें किसी पर भी झूठा आरोप नहीं लगाना चाहिए। हमें किसी के साथ भी धोखा नहीं करना चाहिए। हमें किसी को भी गलत परामर्श देकर उसे मार्ग से विचलित नहीं करना चाहिए। झूठ बोलकर किसी का रिश्ता तय नहीं करना चाहिए। पंचायत अथवा किसी भी और स्थान पर झूठी गवाही नहीं देनी चाहिए। झूठ ही हिंसा को जन्म देता है। सत्य अहिंसा का आधार है।

3. अस्तेय (Asteya)—जैन धर्म में अस्तेय को बहुत महत्त्व दिया गया है। अस्तेय का भाव है चोरी न करना। जैन धर्म में चोरी का अर्थ बहुत विशाल है। किसी की वस्तु चुरा लेनी एक सीधा अपराध है, लेकिन जैन धर्म में उसको चोरी ही माना गया है जो कोई भी व्यक्ति किसी द्वारा भूली हुई वस्तु का प्रयोग भी करता है। हमें किसी की वस्तु उसके मालिक की आज्ञा के बिना नहीं लेनी चाहिए। हमें किसी के घर में भी बिना आज्ञा के प्रवेश नहीं करना चाहिए। गुरु की स्वीकृति के बिना भिक्षा में प्राप्त अनाज को ग्रहण नहीं करना चाहिए। बिना स्वीकृति के हमें किसी के घर निवास नहीं करना चाहिए। यदि घर में रहने की स्वीकृति मिले तो उसकी आज्ञा के बिना उसकी वस्तु को इस्तेमाल नहीं करना चाहिए। जैन धर्म के अनुसार चोरी के दो प्रकार हैं। ये हैं-सूक्ष्म चोरी और स्थूल चोरी। सूक्ष्म चोरी उसको कहते हैं जिस में मनुष्य अपने परिवार के हित के लिए संयम स्वभाव से काम करता है। जैसे जंगल में लकड़ी और फल आदि प्राप्त करना। समाज और कानून की नज़रों में जिस चोरी को दंड योग्य माना जाता है उसको स्थूल चोरी कहा जाता है। मिलावट करनी, चोर की सहायता करनी, चोरी का माल खरीदना, कम मापदंड करना, लोगों से धोखे के सा. अधिक ब्याज प्राप्त करने को स्थूल चोरी कहा जाता है। एक बार चोरी करने वाला मनुष्य ग़रीब घर में जन्म लेता है बार-बार चोरी करने वाला मनुष्य अगले जन्म में गुलाम के रूप में जन्म लेगा।
4. अपरिग्रह (Aparigraha) जैन धर्म में अपरिग्रह महाव्रत को बहुत महत्ता दी गई है। अपरिग्रह से भाव है सांसारिक वस्तुओं के प्रति मोह न रखना। ये सामान्य देखने में आता है कि गृहस्थी लोग आवश्यक वस्तुओं को आवश्यकता से ज्यादा इकट्ठा करते हैं। जीवन की आवश्यक वस्तुओं को इकट्ठा करने में कोई बुराई नहीं, लेकिन वस्तुओं का आवश्यकता से अधिक भंडार इकट्ठा करना वास्तव में अन्य लोगों के अधिकार को मारना है। जितनी अधिक वस्तुओं को इकट्ठा करने की आकांक्षा बढ़ेगी उतना ही मन अशांत रहेगा। ऐसा मनुष्य कभी भी मोक्ष प्राप्त – * कर सकता। आवश्यकता से ज्यादा संपत्ति इकट्ठा करना भी एक अनुचित कर्म है। जैन साधुओं को आवप्रगकता से अधिक भोजन करने, कपड़े पहनने और बिस्तर आदि रखने की मनाही है। इस महाव्रत की पालना करने वाला व्यक्ति मोक्ष को प्राप्त करता है।
5. ब्रह्मचर्या (Brahmacharya)—जैन धर्म में ब्रह्मचर्या महाव्रत को विशेष महत्त्व प्राप्त है। इससे भाव है काम वासना से दूर रहना। जैन साधुओं के लिए इस सम्बन्धी कठोर नियम बनाए गए हैं। उनके लिए ये आवश्यक कि वे किसी स्त्री की ओर न देखें, उनसे बातें न करें, किसी भी स्त्री के साथ भूतकाल में बिताए समय को याद न करें। ऐसे किसी घर में न जाए जहाँ कोई स्त्री अकेली रहती हो। शुद्ध और थोड़ा भोजन खाना चाहिए। इस तरह जैन साधवियों के लिए भी नियम निश्चित हैं। उनके लिए किसी पुरुष के साथ बातचीत करने और उनके बारे में सोचने की मनाही है। ग्रहस्थियों के लिए केवल अपनी स्त्री का साथ करना ही ब्रह्मचर्या है। जैन धर्म में काम को वास्तव में जीवन को समाप्त करने वाला रोग माना गया है।
उपरोक्त पाँच महाव्रतों की पालना करने वाला व्यक्ति संयमी बन जाता है और निर्वाण अथवा मोक्ष प्राप्त करता है। डॉ० के० सी० सोगानी के अनुसार,
“इन पाँच महाव्रतों की पालना व्यक्तिगत और सामाजिक उन्नति के लिए सहायक है।”6
5. “Ahimsa is the sheet anchor of Jainism.” B.B. Luniya, Life and Culture in Ancient India (Agra : 1982) p. 162.
6. “The observance of these five rows is capable of bringing about individual as well as social progress.”: Dr. K.C. Sogani, op. cit., p, 65.
प्रश्न 10.
प्रमुख जैन संप्रदायों के बारे में जानकारी दें।
(Write about the main sects in Jainism.)
उत्तर-
जैनी अनेक संप्रदायों में बंटे हुए हैं। इनमें से कुछ प्रमुख संप्रदायों का संक्षेप वर्णन निम्नलिखित अनुसार—
1. अजीविक (The Ajivika)-इस संप्रदाय का संस्थापक गोशाल था। वह स्वामी महावीर का शिष्य था और 6 वर्षों के पश्चात् उनसे अलग हो गया था। यह संप्रदाय अपने नियति (किस्मत) के विशेष सिद्धांत के लिए प्रसिद्ध है। इसके अनुसार हर वस्तु की किस्मत पहले से ही निश्चित है। इस को मनुष्य के यत्नों के द्वारा बदला नहीं जा सकता। गोशाल के द्वारा प्रचारित धर्म भारत में 13वीं शताब्दी तक प्रफुल्लित रहा और बाद में लोप हो गया।
2. दिगंबर और श्वेतांबर संप्रदाय (The Digambara and Shvetambra Sects)-जैन धर्म के सब संप्रदायों में से दिगंबर और श्वेतांबर संप्रदाय सबसे अधिक प्रसिद्ध थे। चंद्रगुप्त मौर्य के शासन काल के समय मगध में भयंकर अकाल पड़ा था। इसलिए भद्रबाहु जो जैनी भिक्षुकों का नेता था अपने साथ बहुत सारे भिक्षुओं को लेकर मैसूर (कर्नाटक) चला गया। जो भिक्षुक मगध में रह गये थे उन्होंने स्थूलभद्र को अपना मुखिया चुन लिया। इन भिक्षुकों ने पाटलिपुत्र में एक सभा का आयोजन किया और अपने साहित्य को एक नया रूप दिया। इस साहित्य को उन्होंने अंग का नाम दिया। इसके अतिरिक्त इन भिक्षुओं ने नंगे रहने की प्रथा को त्याग दिया और सफ़ेद कपड़े पहनने शुरू कर दिये। 12 वर्षों के पश्चात् जब भद्रबाहु अपने अन्य भिक्षुकों के साथ दुबारा मगध आया तो उसने स्थूलभद्र द्वारा किए गए परिवर्तनों को स्वीकार न किया। परिणामस्वरूप जैनी दो संप्रदायों दिगंबर और श्वेतांबर में बाँटे गए। दिगंबर से भाव था नग्न रहने वाले और श्वेतांबर से भाव था सफ़ेद वस्त्र पहनने वाले। इन दोनों में प्रमुख अंतर निम्नलिखित हैं—
- दिगंबर संप्रदाय वाले नंगे रहते थे जबकि श्वेतांबर जाति वाले सफ़ेद वस्त्र पहनते थे।
- दिगंबर संप्रदाय वालों का कहना है कि स्त्रियाँ तब तक मोक्ष प्राप्त नहीं कर सकतीं जब तक वे पुरुष के रूप में जन्म नहीं लेती। श्वेतांबर संप्रदाय वाले इस सिद्धांत को गलत मानते हैं। उनका कहना है कि स्त्रियाँ इसी जन्म में मोक्ष प्राप्त कर सकती हैं।
- दिगंबर संप्रदाय वाले स्त्रियों को जैन संघ में शामिल होने की आज्ञा नहीं देते। दूसरी ओर श्वेतांबर संप्रदाय वाले स्त्रियों पर ऐसी कोई पाबंदी नहीं लगाते। उनका कहना था कि 19वीं तीर्थंकर मल्ली एक स्त्री थी। दिगंबर संप्रदाय वाले इस बात का खंडन करते हैं।
- दिगंबर संप्रदाय वालों का कहना है कि स्वामी महावीर ने विवाह नहीं करवाया था। श्वेतांबर संप्रदाय वाले यह मानते हैं कि स्वामी महावीर ने विवाह करवाया था। उनकी एक पुत्री थी, जिसका नाम प्रियादर्शना था।
- दिगंबर संप्रदाय वालों का यह मत है कि ज्ञान प्राप्त करने वाले साधुओं को भोजन की ज़रूरत नहीं रहती जबकि श्वेतांबर मत वाले इस बात का खंडन करते हैं।
- दिगंबर और श्वेतांबर संप्रदाय वालों का धार्मिक साहित्य अलग-अलग है।
- दिगंबर संप्रदाय वालों की मूर्तियाँ नंगेज होती हैं जबकि श्वेतांबर संप्रदाय वालों की मूर्तियों को कपड़े पहनाये जाते हैं और उनको गहनों से सजाया जाता है।
3. लोक संप्रदाय (Lonka Sect)-इस संप्रदाय का मुखिया लोंक सा था। वह अहमदाबाद का रहने वाला था। 1474 ई० में एक जैनी साधु ज्ञान जी ने कुछ धार्मिक जैनी ग्रंथों का उतारा करने के लिए लोक सा को कहा। इन ग्रंथों को पढ़ते समय लोंक सा ने देखा कि मूर्ति पूजा का वर्णन कहीं भी नहीं आया जबकि जैनी कई सदियों से मूर्ति पूजा करते आ रहे थे। इसलिए उसने जैन धर्म में प्रचलित मूर्ति पूजा का खंडन किया। इससे जैनियों में एक बड़ा विवाद शुरू हो गया ? भानाजी लोंक सा के मत से सहमत हुआ और इस तरह वह लोंक सा संप्रदाय का पहला आचार्य बना।
4. स्थानकवासी (Sthanakvasi)-इस संप्रदाय का संस्थापक वीराजी था। वह सूरत का रहने वाला था। इस नए संप्रदाय का नाम स्थानकवासी इसलिए पड़ा क्योंकि इस संप्रदाय के साधु मंदिरों की जगह मठों में रहते थे। वे बहुत ही सादा जीवन व्यतीत करते थे। वे मूर्ति पूजा और तीर्थ यात्राओं में विश्वास नहीं रखते थे।
5. तेरा पंथ (Terapanth)-इंस संप्रदाय के संस्थापक मारवाड़ के भीखनजी थे। इसकी स्थापना 1706 ई० में की गई थी। इस संप्रदाय के तेरह धार्मिक नियम थे जिस कारण इस संप्रदाय का नाम तेरा पंथ पड़ा। यह संप्रदाय भी मूर्ति पूजा में विश्वास नहीं रखता। यह तप और अनुशासन पर बहुत ज़ोर देता है।
6. तारना पंथ (Taranapanina)-इस पंथ की स्थापना स्वामी तारना ने ग्वालियर में की थी। इस पंथ को मानने वाले मूर्ति पूजा, धर्म के बाहरी दिखावे और जाति भेदों के विरुद्ध हैं। उनके अपने अलग मंदिर हैं जिनमें मूर्तियाँ ही नहीं बल्कि पवित्र धार्मिक ग्रंथों की पूजा भी की जाती है।

प्रश्न 11.
जैन मत के प्रमुख संप्रदाय कौन से हैं ? उनके मध्य समानताएँ तथा भिन्नताएँ स्पष्ट करें।
(What are the main sects in Jainism ? Explain their similarities and differences.)
अथवा
जैन धर्म के फिरके दिगंबर और श्वेतांबर के बारे में जानकारी दीजिए।
(Describe the sects Digambara and Shvetambra of Jainism.)
उत्तर-
दिगंबर और श्वेतांबर संप्रदाय (The Digambara and Shvetambra Sects)-जैन धर्म के सब संप्रदायों में से दिगंबर और श्वेतांबर संप्रदाय सबसे अधिक प्रसिद्ध थे। चंद्रगुप्त मौर्य के शासन काल के समय मगध में भयंकर अकाल पड़ा था। इसलिए भद्रबाहु जो जैनी भिक्षुकों का नेता था अपने साथ बहुत सारे भिक्षुओं को लेकर मैसूर (कर्नाटक) चला गया। जो भिक्षुक मगध में रह गये थे उन्होंने स्थूलभद्र को अपना मुखिया चुन लिया। इन भिक्षुकों ने पाटलिपुत्र में एक सभा का आयोजन किया और अपने साहित्य को एक नया रूप दिया। इस साहित्य को उन्होंने अंग का नाम दिया। इसके अतिरिक्त इन भिक्षुओं ने नंगे रहने की प्रथा को त्याग दिया और सफ़ेद कपड़े पहनने शुरू कर दिये। 12 वर्षों के पश्चात् जब भद्रबाहु अपने अन्य भिक्षुकों के साथ दुबारा मगध आया तो उसने स्थूलभद्र द्वारा किए गए परिवर्तनों को स्वीकार न किया। परिणामस्वरूप जैनी दो संप्रदायों दिगंबर और श्वेतांबर में बाँटे गए। दिगंबर से भाव था नग्न रहने वाले और श्वेतांबर से भाव था सफ़ेद वस्त्र पहनने वाले। इन दोनों में प्रमुख अंतर निम्नलिखित हैं—
- दिगंबर संप्रदाय वाले नंगे रहते थे जबकि श्वेतांबर जाति वाले सफ़ेद वस्त्र पहनते थे।
- दिगंबर संप्रदाय वालों का कहना है कि स्त्रियाँ तब तक मोक्ष प्राप्त नहीं कर सकतीं जब तक वे पुरुष के रूप में जन्म नहीं लेती। श्वेतांबर संप्रदाय वाले इस सिद्धांत को गलत मानते हैं। उनका कहना है कि स्त्रियाँ इसी जन्म में मोक्ष प्राप्त कर सकती हैं।
- दिगंबर संप्रदाय वाले स्त्रियों को जैन संघ में शामिल होने की आज्ञा नहीं देते। दूसरी ओर श्वेतांबर संप्रदाय वाले स्त्रियों पर ऐसी कोई पाबंदी नहीं लगाते। उनका कहना था कि 19वीं तीर्थंकर मल्ली एक स्त्री थी। दिगंबर संप्रदाय वाले इस बात का खंडन करते हैं।
- दिगंबर संप्रदाय वालों का कहना है कि स्वामी महावीर ने विवाह नहीं करवाया था। श्वेतांबर संप्रदाय वाले यह मानते हैं कि स्वामी महावीर ने विवाह करवाया था। उनकी एक पुत्री थी, जिसका नाम प्रियादर्शना था।
- दिगंबर संप्रदाय वालों का यह मत है कि ज्ञान प्राप्त करने वाले साधुओं को भोजन की ज़रूरत नहीं रहती जबकि श्वेतांबर मत वाले इस बात का खंडन करते हैं।
- दिगंबर और श्वेतांबर संप्रदाय वालों का धार्मिक साहित्य अलग-अलग है।
- दिगंबर संप्रदाय वालों की मूर्तियाँ नंगेज होती हैं जबकि श्वेतांबर संप्रदाय वालों की मूर्तियों को कपड़े पहनाये जाते हैं और उनको गहनों से सजाया जाता है।
प्रश्न 12.
जैन संघ की मुख्य विशेषताओं का वर्णन करो। (Explain the salient features of Jain Sangha.)
अथवा
जैन धर्म के संघ-अनुशासन के बारे में चर्चा कीजिए।
(Discuss the Sangha discipline of Jainism.)
उत्तर-
जैन संघ की स्थापना स्वामी महावीर जी ने पावा नगर में की थी। इसने जैन धर्म के प्रसार में प्रशंसनीय योगदान दिया।
1. सदस्य (Member)-जैन संघ में चार प्रकार के लोग शामिल होते हैं जिनको भिक्षु और भिक्षुणियाँ तथा श्रावक और श्राविका कहा जाता था। भिक्षु और भिक्षुणियाँ वे थे जिन्होंने संसार का त्याग कर दिया था। श्रावक और श्राविका वे थे जो गृहस्थी का जीवन व्यतीत करते थे।
2. दीक्षा (Initiation)—जो व्यक्ति संघ में शामिल होना चाहता था उसको अपने माता-पिता और संरक्षक से आज्ञा लेनी पड़ती थी। इसके बाद वह अपना मुंडन करके, स्नान करके, सफ़ेद कपड़े पहन के भिक्षा का बर्तन लेकर किसी प्रमुख जैन आचार्य के पास जा कर दीक्षा लेता था। इस संस्कार को निष्कर्म संस्कार कहते थे। स्त्रियाँ भी जैन संघ में शामिल हो सकती थीं। जैन संघ के दरवाज़े सभी जातियों के लिए खुले थे। केवल अधर्मी व्यक्तियों को संघ में प्रवेश करने की आज्ञा नहीं थी।
3. अनुशासित जीवन (Disciplined Life)-दीक्षा प्राप्त करने के बाद भिक्षु-भिक्षुणियों को बहुत अनुशासित जीवन व्यतीत करना पड़ता था। उनको पाँच महाव्रतों, अहिंसा, सुनित, अस्तेय, अपरिगृह और ब्रह्मचर्य का पालन करना पड़ता था। उनको मन, वचन और शरीर से किसी को भी हिंसा पहुँचाने की मनाही थी। उनको झूठ बोलने, चोरी करने, अपने पास संपत्ति रखने, सुगंधित वस्तुओं का प्रयोग करने, जूते, छाता, पलंग और कुर्सी आदि का प्रयोग करने, बिना आज्ञा किसी के घर जाने, गृहस्थी के बर्तनों में भोजन करने, अधिक खाने, रात हो जाने के बाद भोजन करने, किसी की निंदा करने, किसी स्त्री के साथ बातचीत करने, जिस घर में स्त्री हो वहाँ ठहरने आदि की सख्त मनाही थी। गृहस्थी व्यक्तियों को भी यद्यपि इन नियमों का पालन करने के लिए कहा गया है, परंतु उन पर इतनी सख्ती लागू नहीं की गई थी।
4. प्रतिदिन जीवन (Daily Life)-प्रत्येक भिक्षु अथवा भिक्षुणी अपने रोज़ाना जीवन को 8 भागों में बाँटता था। इनमें 4 भाग धार्मिक ग्रंथों की पढ़ाई के लिए, 2 तप के लिए, 1 खाने के लिए और 1 आराम करने के लिए निश्चित होता था। वे अपना भोजन प्रतिदिन माँग कर खाते थे। उनको एक से अधिक घर से भिक्षा लेने की मनाही थी। जैन संघ के सारे सदस्य वर्षा के चार महीनों में एक स्थान पर रह कर जैन धर्म का प्रचार करते थे। बाकी के आठ महीने वे अलग-अलग स्थानों पर जा कर जैन धर्म के प्रचार में व्यतीत करते थे।
5. जैन संघ का मुखिया (Chief of the Jain Sangha)-जैन संघ का मुखिया आचार्य कहलाता था। वह संघ के सारे भिक्षुओं पर नियंत्रण रखता था। केवल उसी को ही दीक्षा देने, संघ का सदस्य बनाने अथवा किसी को सज़ा देने का अधिकार था। इस पदवी के लिए बहुत ही सुलझे हुए और उच्च चरित्र के व्यक्ति को नियुक्त किया जाता था। स्त्रियों के अपने अलग संघ होते थे। इसके प्रमुख को प्रवर्तिनी कहा जाता था। उसका प्रमुख कार्य जैन संघ में अनुशासन स्थापित रखना था।
6. जैन संघ की भूमिका (Role of Jain Sangha)-जैन संघ ने भारत में जैन धर्म को लोकप्रिय बनाने में महत्त्वपूर्ण भूमिका निभाई। जैन संघ में सम्मिलित होने वाले भिक्षुओं एवं भिक्षुणियों ने जैन धर्म के प्रसार के लिए कोई प्रयास शेष नहीं छोड़ा। प्रसिद्ध लेखक एस० सी० रैचौधरी के अनुसार,
“वास्तव में जैन संघ के प्रयासों के कारण जैन धर्म ने भारत की भूमि में अपनी गहरी जड़ें बना लीं तथा यह आज भी कायम हैं।”7
7. “In fact, it is mainly due to their efforts that Jainism took root into Indian soil and still survives,” S.C. Raychoudhary, History of Ancient India (Delhi : 2006) p. 107.
प्रश्न 13.
जैन धर्म ग्रंथों की भाषा क्या है ? जैन धर्म ग्रंथों के बारे में प्रारंभिक जानकारी दें।
(What is the language of Jain scriptures ? Give preliminary information about Jain scriptures.)
अथवा
जैन धर्म ग्रंथों के बारे में प्रारंभिक जानकारी दें।
(Give preliminary information about the major Jain scriptures.)
अथवा
जैन मत के प्रमुख धार्मिक ग्रंथों की जानकारी दो। (Give information about the prominent scriptures of Jainism.)
अथवा
जैन धर्म के प्रमुख ग्रंथों के बारे में आप क्या जानते हो ?
(What do you know about the prominent scriptures of Jainism ?)
अथवा
प्रमुख जैन धार्मिक ग्रंथों पर प्रकाश डालें।
(Throw light on the prominent Jain scriptures.)
उत्तर-
जैनियों ने अनेक धार्मिक ग्रंथों की रचना की। इनमें से जो ग्रंथ हमें आज उपलब्ध हैं उनकी संख्या 45 है। ये सारे ग्रंथ जैन धर्म के श्वेतांबर संप्रदाय के साथ संबंधित हैं। ये ग्रंथ प्राकृत अथवा अर्ध मगधी जो उस समय लोगों की बोलचाल की आम भाषा थी में लिखे गए हैं। इन ग्रंथों को गुजरात में वल्लभी के स्थान पर 5वीं शताब्दी में लिखित रूप दिया गया। इनको एक प्रसिद्ध जैनी साधु देवरिद्धी ने संपूर्ण किया। इन ग्रंथों को 6 वर्गों में बाँटा गया है। इनके नाम हैं—
(1) 12 अंम
(2) 12 उपांग
(3) 10 प्राकिरण
(4) 6 छेदसूत्र
(5) 4 मूलसूत्र
(6) 2 विविध पुस्तकें।
इनका संक्षेप वर्णन निम्नलिखित अनुसार है—
1. 12 अंग (The Twelve Angas)-जैनियों के धार्मिक ग्रंथों में 12 अंगों को सब से अधिक पवित्र समझा जाता है। इन अंगों के नाम और उनका संक्षेप वर्णन इस प्रकार है
- आचारांग सूत्र-इसमें जैन भिक्षुओं और भिक्षुणियों के लिए नियमों का वर्णन किया गया है। इसमें महावीर के जीवन का भी वर्णन मिलता है।
- सूत्रक्रितांग- इसमें कर्म और अहिंसा के सिद्धांतों के बारे में और नरक के दु:खों के बारे में वर्णन मिलता है। इनके अतिरिक्त इसमें विरोधी धर्मों के सिद्धांतों का खंडन इस उद्देश्य से किया गया है ताकि जैनियों का अपने धर्म में पक्का विश्वास रहे।
- स्थानांग-इसमें जैन धर्म के अलग-अलग विषयों के बारे जानकारी दी गई है।
- समवायांग-इसमें जैन सिद्धांतों का संख्यात्मक ढंग से वर्णन किया गया है।
- भगवती सूत्र-इसको जैन धार्मिक साहित्य का सबसे महत्त्वपूर्ण ग्रंथ समझा जाता है। इसमें जैन सिद्धांतों का प्रश्न-उत्तर रूप में वर्णन किया गया है। ये प्रश्न स्वामी महावीर के प्रमुख शिष्य गौतम इंद्रभूति द्वारा पूछे गये थे और इनका उत्तर स्वामी महावीर ने स्वयं दिया था।
- ज्ञात धर्म कथा-इसमें जैन धर्म से संबंधित प्रसिद्ध कथाओं का वर्णन मिलता है। इन कथाओं को उदाहरणों सहित समझाया गया है।
- उपासकदशा-इसमें स्वामी महावीर के समय के 10 उन अमीर व्यक्तियों की कहानियाँ दी गई हैं जो महावीर के शिष्य बन गए थे और जिन्होंने कठोर तपस्या के बाद मोक्ष प्राप्त किया।
- अंतक्रिदशा-इसमें उन जैन मुनियों के जीवन का वर्णन मिलता है जिन्होंने कठोर तप के बाद मोक्ष प्राप्त किया।
- अनउत्तरोपपातिक-इसमें भी कुछ जैन मुनियों के जीवन का वर्णन मिलता है।
- प्रश्न व्याकरण- इसमें पाँच महाव्रतों और पाँच अणुव्रतों का वर्णन किया गया है।
- विपाकसूत्र-इसमें अच्छे या बुरे कर्मों से मिलने वाले फलों का वर्णन किया गया है।
- दृष्टिवाद-यह अंग अब लोप हो चुका है। अन्य ग्रंथों में से इस अंग से संबंधित मिलते विवरणों के आधार पर कहा जा सकता है कि इसमें विभिन्न सिद्धांतों का संक्षेप वर्णन किया गया था।
2. 12 उपांग (The Twelve Upangas)-प्रत्येक अंग का एक-एक उपांग है। इनमें मिथिहासिक कथाओं का अधिक वर्णन मिलता है। इनसे ज्योतिष, भूगोल और ब्रह्मांड आदि के संबंध में जानकारी प्राप्त होती है। कहीं-कहीं ऐतिहासिक घटनाओं का भी जिक्र आता है। 12 उपांगों में राज्य प्रश्नीय नामक उपांग सब से अधिक प्रसिद्ध है। इसमें जैन मुनी केश और पायोस नामक राजा के मध्य हुई वार्तालाप का विवरण लिखा हुआ है।
3. 10 प्राकिरण (The Ten Prakirans)-इनमें जैन धर्म से संबंधित विभिन्न विषयों को पद्य रूप में लिखा गया है। इनसे स्वामी महावीर के जीवन और उसके उपदेशों संबंधी महत्त्वपूर्ण जानकारी प्राप्त होती है।
4. 6 छेदसूत्र (The Six Chhedasutras)-इनमें जैन भिक्षुओं और भिक्षुणियों के आचार से संबंधित नियमों का वर्णन किया गया है। छेदसूत्रों में कल्पसूत्र को सबसे प्रसिद्ध माना जाता है। इसकी रचना भद्रबाह ने की थी। इसमें स्वामी महावीर की जीवन कथा का विस्तारपूर्वक वर्णन किया गया है।
5. 4 मूलसूत्र (The Four Mulasutras)-4 मूलसूत्रों को जैनी साहित्य में बहुमूल्य समझा जाता है। इनमें जैन धर्म से संबंधित कथाओं और उनसे मिलने वाली शिक्षा, जैन संघ के नियमों और कुछ जैन मुनियों के जीवन तथा उनके उपदेशों के बारे जानकारी प्राप्त होती है। ये सारे मूलरूप में लिखे गये हैं। मूलसूत्रों में उत्तर अध्ययन नामक सूत्र को सबसे महत्त्वपूर्ण समझा जाता है।
6. 2 विविध पुस्तकें (Two Miscellaneous Texts)—इनमें नंदीसूत्र और अनुयोगद्वार नामक पुस्तकें शामिल हैं। ये एक प्रकार से विश्वकोष हैं। इनमें जैन धर्म की विभिन्न शाखाओं, धार्मिक सिद्धांतों, अर्थशास्त्र और काम शास्त्र के विषयों के संबंध में जानकारी दी गई है।

प्रश्न 14.
जैन धर्म का भारतीय सभ्यता को क्या योगदान है ? (What is the Legacy of Jainism to Indian Civilization ?)
उत्तर-
इसमें कोई शक नहीं कि जैन धर्म बौद्ध धर्म की तरह उन्नत हो सका परंतु फिर भी इसने भारत में सामाजिक, धार्मिक, सांस्कृतिक और राजनीतिक क्षेत्रों में अपनी गहरी छाप छोड़ी।।
1. सामाजिक क्षेत्र में योगदान (Legacy in the Social Field) सामाजिक क्षेत्र में जैनियों ने बहुत महत्त्वपूर्ण भूमिका निभाई। छठी शताब्दी में हिंदू धर्म में जाति प्रथा बड़ी कठोर हो गई थी। एक जाति के लोग दूसरी जाति के लोगों से सख्त नफ़रत करते थे। शूद्र जाति के लोगों के साथ जानवरों से भी बुरा व्यवहार किया जाता था। महावीर ने जाति प्रथा का ज़ोरदार शब्दों में खंडन किया। उन्होंने अपने धर्म में प्रत्येक धर्म से संबंधित लोगों को शामिल किया। उन्होंने लोगों में आपसी भाईचारे और बराबरी का प्रचार किया। परिणामस्वरूप वह लोगों में फैली आपसी घृणा को काफी सीमा तक दूर करने में सफल हुए। इस प्रकार जैनियों ने भारतीय समाज को एक नया रूप दिया।
2. धार्मिक क्षेत्र में योगदान (Legacy in the Religious Field)-धार्मिक क्षेत्र में भी जैनियों का योगदान बहुत प्रशंसनीय था। जैन धर्म ने लोगों को सादा और पवित्र जीवन व्यतीत करने के लिए प्रेरित किया। जैन धर्म में फ़िजूल के रीति-रिवाजों, यज्ञों और बलियों आदि के लिए कोई स्थान नहीं था। जैन धर्म के यत्नों के कारण धार्मिक क्षेत्र में फैले बहुत सारे अंध-विश्वासों का अंत हो गया। जैन धर्म की बढ़ती हुई प्रसिद्धि को देखकर हिंदू धर्म के नेताओं ने अपने धर्म को सुरजीत करने के उद्देश्य से अपने धर्म में आवश्यक सुधार किए।
3. सांस्कृतिक क्षेत्र में योगदान (Legacy in the Cultural Field)—सांस्कृतिक क्षेत्र में भी जैन धर्म का योगदान बहुत महत्त्वपूर्ण था। जैन धर्म के सिद्धांतों ने अपने ग्रंथ प्राकृत, गुजराती, हिंदी, मराठी, कन्नड़ और तामिल भाषाओं में लिखे। परिणामस्वरूप इन क्षेत्रीय भाषाओं को बहुत उत्साह मिला। इन ग्रंथों में यद्यपि धर्म से संबंधित बातें लिखी गई हैं पर फिर भी इनसे हमें उस समय की भारत की सामाजिक और राजनीतिक स्थिति के बारे में महत्त्वपूर्ण जानकारी प्राप्त होती है। इस कारण इन जैनी ग्रंथों को भारतीय इतिहास का एक अमूल्य स्रोत माना जाता है। जैनियों ने कई प्रभावशाली और प्रसिद्ध मंदिरों का निर्माण करवाया। इन मंदिरों में कई बहुत मनमोहक मूर्तियाँ रखी जाती थीं। राजस्थान में माऊँट आबू और कर्नाटक में श्रावण बेलगोला में बने जैनियों के मंदिर अपनी भूवन निर्माण कला के कारण न केवल भारत में बल्कि दुनिया भर में प्रसिद्ध हैं। इनके अतिरिक्त जैनियों ने भारत में कई प्रसिद्ध स्तूपों का निर्माण भी करवाया।
4. लोक कल्याण के क्षेत्र में योगदान (Legacy in the Field of Public Welfare)-स्वामी महावीर ने अपने शिष्यों को समाज सेवा का उपदेश दिया था। इसी कारण जैनमत वालों ने लोगों की सहायता के लिए बहुत सी धर्मशालाएँ बनाईं। शिक्षा के प्रचार के लिए शिक्षा संस्थाओं की स्थापना की, मनुष्यों और पशुओं के इलाज के लिए कई अस्पताल खुलवाए और कई अन्य लोक कल्याण के कार्य भी किए। जैनियों द्वारा स्थापित की गई कई शिक्षा संस्थाएँ आज भी प्रसिद्ध हैं। उनके द्वारा खोले गए अस्पतालों में आज भी ग़रीब रोगियों का मुफ्त इलाज होता है और जानवरों की देखभाल की जाती है।
5. राजनीतिक क्षेत्र में योगदान (Legacy in the Political Field) जैन मत में अहिंसा के सिद्धांत पर बहुत ज़ोर दिया जाता था। इसने लोगों को शांतमयी जीवन व्यतीत करने की प्रेरणा दी। परिणामस्वरूप कई राजाओं ने लड़ाई में हिस्सा लेना बंद कर दिया ताकि निर्दोष लोगों का खून न बहाया जाये। वे शांतिप्रिय बन गए। इसी कारण भारत में काफी समय तक शाँति और खुशहाली का वातावरण रहा परंतु दूसरी ओर इसका भारतीय राजनीति पर कुछ बुरा प्रभाव भी पड़ा। युद्धों में भाग न लेने के कारण भारतीय सेना कमजोर हो गई। परिणामस्वरूप वह बाद में होने वाले विदेशी आक्रमणों का डट कर मुकाबला न कर सकी। इसी कारण भारतीयों को सैंकड़ों वर्षों तक गुलामी का जीवन व्यतीत करना पड़ा।
समूचे रूप में हम यह कह सकते हैं कि जैनियों ने भारतीय समाज को कई क्षेत्रों में बहुमूल्य योगदान दिया। अंत में हम डॉक्टर वी० ए० मंगवी के इन शब्दों से सहमत हैं,
“वास्तव में भारत में जैनियों की सबसे प्रमुख विशेषता भारतीय संस्कृति को दिया गया उनका बहुमूल्य योगदान का रिकार्ड है। उनकी सीमित एवं थोड़ी जनसंख्या को देखते हुए जैनियों ने जो योगदान भारतीय संस्कृति के विभिन्न पक्षों को दिया वह वास्तव में महान् है।”8
8. “In fact, the most outstanding characteristic of Jainism in India is their very impressive record of contributions to Indian culture in comparison with the limited and small population of Jains, the achievements of Jains in enriching the various aspects of Indian culture are re great.” Dr. V.A. Sangve, Aspects of Jaina Religion (New Delhi: 1990) p. 98.
लघु उत्तरीय प्रश्न
प्रश्न 1.
तीर्थंकर से क्या अभिप्राय है ? (What do you mean by Tirthankara ?)
उत्तर-
जैन आचार्यों को तीर्थंकर कहा जाता है। तीर्थंकर से अभिप्राय है संसार के भवसागर से पार करने वाला गुरु। जैन धर्म में कुल 24 तीर्थंकर हुए हैं। पहले तीर्थंकर का नाम ऋषभनाथ था। 23वां तीर्थंकर पार्श्वनाथ था। वह स्वामी महावीर के जन्म से 250 वर्ष पहले हुए। 24वें तीर्थंकर स्वामी महावीर थे। उनको जैन धर्म का वास्तविक संस्थापक माना जाता है। उनके समय में जैन धर्म ने अद्वितीय विकास किया।
प्रश्न 2.
पार्श्वनाथ। (Parshvanatha.)
उत्तर-
पार्श्वनाथ जैन धर्म का 23वां तीर्थंकर था। उसकी मुख्य शिक्षाएँ यह थीं—
- सजीव वस्तुओं को कष्ट न पहुँचायें (अहिंसा)।
- झूठ न बोलो (सुनृत)।
- बिना दिये कुछ न लो (अस्तेय)।
- सांसारिक पदार्थों से मोह न करो (अपरिग्रह)। 777 ई० पू० के लगभग उन्होंने बिहार के माऊँट समेता नामक पहाड़ी पर निर्वाण प्राप्त किया।
प्रश्न 3.
स्वामी महावीर। (Lord Mahavira.)
उत्तर-
स्वामी महावीर का जन्म 599 ई० पू० वैशाली के निकट कुंडग्राम में हुआ। आपके पिता जी का नाम सिद्धार्थ तथा माता जी का नाम त्रिशला था। महावीर के बचपन का नाम वर्द्धमान था। महावीर की शादी एक सुंदर राजकुमारी यशोदा से हुई। महावीर ने 30 वर्षों की आयु में गृह त्याग दिया था। उन्होंने 12 वर्ष तक घोर तपस्या के पश्चात् ज्ञान प्राप्त किया। आपने 30 वर्षों तक अपने ज्ञान का प्रसार किया। राजगृह, वैशाली, कौशल, मिथला, विदेह तथा अंग उनके प्रसिद्ध प्रचार केंद्र थे। 527 ई० पू० उन्होंने पावा में निर्वाण प्राप्त किया।
प्रश्न 4.
भगवान महावीर की शिक्षाओं के बारे में चर्चा कीजिए। (Discuss about the teachings of Lord Mahavira.)
अथवा
स्वामी महावीर की शिक्षाएँ। (Teachings of Lord Mahavira.)
उत्तर-
स्वामी महावीर ने अपने अनुयायियों को तीन रत्नों पर चलने के लिए कहा। उन्होंने कठोर तप, अहिंसा तथा उच्च आचरण पर जोर दिया। वह समानता, आवागमन तथा कर्म सिद्धांत में विश्वास रखते थे। वह ईश्वर, यज्ञों, बलियों, वेद तथा संस्कृत में विश्वास नहीं रखते थे। उनके अनुसार प्रत्येक जैनी को अपने जीवन में पाँच महाव्रतों की पालना करनी चाहिए। उनके अनुसार मानव जीवन का अंतिम उद्देश्य निर्वाण प्राप्त करना है।
प्रश्न 5.
त्रि-रत्न। (Tri-Ratna.)
अथवा
त्रि-रत्न क्या हैं ? (What is Tri-Ratna ?)
उत्तर-
स्वामी महावीर जी ने अपने अनुयायियों को तीन रत्नों पर चलने के लिए कहा। ये त्रि-रत्न थे-सच्ची श्रद्धा, सच्चा ज्ञान तथा शुद्ध आचरण। पहले रत्न के अनुसार प्रत्येक व्यक्ति को 24 तीर्थंकरों में अटल विश्वास होना चाहिए। दूसरे रत्नानुसार जैनियों को सच्चा और पूर्ण ज्ञान प्राप्त करना चाहिए तथा इनको व्यर्थ के रीति-रिवाज़ों में विश्वास नहीं रखना चाहिए। तीसरे रत्नानुसार प्रत्येक व्यक्ति को सच्चे आचार के अनुसार अपना जीवन व्यतीत करना चाहिए। इनमें से किसी एक ही अनुपस्थिति मनुष्य को उसकी मंज़िल तक नहीं पहुँचा सकती।
प्रश्न 6.
अहिंसा। (Ahimsa.)
उत्तर-
जैन धर्म में अहिंसा की नीति को जितना महत्त्व दिया गया है, उतना विश्व के किसी अन्य धर्म में नहीं दिया गया। अगर अहिंसा को जैन धर्म की आधारशिला कहा जाए तो इसमें कोई संदेह नहीं होगा। अहिंसा से अभिप्राय है कि किसी भी जैव वस्तु को कष्ट न देना। जैन दर्शन के अनुसार मनुष्यों और पशुओं के अतिरिक्त वृक्षों तथा पत्थरों में भी आत्मा का निवास होता है। इस कारण हमें किसी जीव या निर्जीव को कष्ट नहीं देना चाहिए। इसी उद्देश्य से जैनी नंगे पाँव चलते हैं, मुँह पर पट्टी बाँधते हैं, पानी छान कर पीते हैं और सूर्य छिपने के पश्चात् भोजन नहीं करते।
प्रश्न 7.
स्वामी महावीर की शिक्षा के अनुसार एक जैन भिक्षु को कैसा जीवन व्यतीत करना पड़ता था ? (According to the teachings of Lord Mahavira how a Jaina monk led his life ?)
उत्तर-
- स्वामी महावीर की शिक्षा के अनुसार जैन भिक्षुओं को बहुत स्वच्छ जीवन व्यतीत करना पड़ता था।
- प्रत्येक भिक्षु को पाँच प्रतिज्ञाओं की पालना करनी पड़ती थी।
- प्रत्येक भिक्षु को सदैव सत्य बोलना चाहिए। उनको अहिंसा की नीति की पालना करनी पड़ती थी।
- प्रत्येक भिक्षु के लिए आवश्यक था कि उनकी वेशभूषा और खाना-पीना बिल्कुल सादा हो।
प्रश्न 8.
स्वामी महावीर जी की शिक्षाओं का साधारण मनुष्य के जीवन के लिए क्या महत्त्व था ?
(What was the importance of the teachings of Lord Mahavira in the life of a common man ?)
उत्तर-
स्वामी महावीर जी की शिक्षाएँ साधारण मनुष्य के लिए महत्त्वपूर्ण थीं। भगवान् महावीर ने अपने धर्म में बिना किसी भेद-भाव के प्रत्येक वर्ग के लोगों को शामिल किया। इससे समाज में प्रचलित परस्पर घृणा बहुत सीमा तक दूर हुई और लोगों में परस्पर बंधुत्व एवं प्रेम-भाव बढ़ गया। स्वामी महावीर जी ने समाज में प्रचलित अंध-विश्वासों का जोरदार शब्दों में खंडन किया। साधारण लोग भी इन परंपराओं के विरुद्ध थे। इसलिए उनके हृदयों पर स्वामी महावीर जी की शिक्षाओं का गहरा प्रभाव पड़ा। स्वामी महावीर जी ने लोगों को समाज सेवा का उपदेश दिया।
प्रश्न 9.
स्वामी महावीर ने कौन-सी धार्मिक तथा सामाजिक बुराइयों का खंडन किया ? (Which religious and social evils were condemned by Lord Mahavira ?)
उत्तर-
स्वामी महावीर ने यज्ञों, बलियों, पुरोहितवाद तथा धर्म के बाहरी दिखावों का जोरदार शब्दों में खंडन किया। वह मूर्ति पूजा के विरुद्ध थे। उनको वेदों तथा संस्कृत भाषा की पवित्रता में विश्वास नहीं था। वह जाति प्रथा तथा समाज में प्रचलित अन्य रूढ़िवादी विचारों के घोर विरोधी थे। उन्होंने इन रीतियों को एक ढोंग बताया तथा कहा कि कोई भी व्यक्ति इनका पालन करने से निर्वाण को प्राप्त नहीं कर सकता।

प्रश्न 10.
दिगंबर। (Digambaras.)
उत्तर-
दिगंबर जैनियों का एक प्रमुख संप्रदाय है। दिगंबर से अभिप्राय है नग्न रहने वाले। इस संप्रदाय के भिक्षु नग्न रहते हैं। इस संप्रदाय को मानने वालों का कहना है कि स्त्रियाँ तब तक मोक्ष प्राप्त नहीं कर सकती जब तक वे पुरुष के रूप में जन्म नहीं, लेतीं। उन्हें जैन संघ में शामिल होने की आज्ञा नहीं दी जा सकती। इस संप्रदाय का कहना है कि स्वामी महावीर ने विवाह नहीं करवाया था। इनका अपना अलग साहित्य है।
प्रश्न 11.
श्वेतांबर। (Svetambaras.)
उत्तर-
श्वेतांबर जैन धर्म का एक प्रमुख संप्रदाय है। श्वेतांबर से अभिप्राय है सफेद वस्त्र धारण करने वाले। इस कारण इस संप्रदाय के लोग सफेद वस्त्र पहनते हैं। इस संप्रदाय के लोगों का कहना है कि स्त्रियाँ इसी जन्म में ही मुक्ति प्राप्त कर सकती हैं। वे स्त्रियों को जैन संघ में शामिल होने की आज्ञा देते थे। उनका कहना है कि स्वामी महावीर ने विवाह करवाया था। इस संप्रदाय का अपना अलग साहित्य है।
प्रश्न 12.
जैन धर्म भारत में लोकप्रिय क्यों नहीं हो सका ? (Why could not Jainism become popular in India ?)
उत्तर-
जैन धर्म की शिक्षाएँ यद्यपि सरल थीं, परंतु कई कारणों से यह धर्म लोगों में लोकप्रिय न हो सका। पहला, जैन धर्म वालों ने अपने धर्म के प्रचार के लिए कोई विशेष प्रयत्न नहीं किया। दूसरा, जैन धर्म को बौद्ध धर्म की भाँति राजकीय संरक्षण प्राप्त नहीं हो सका। तीसरा, जैन धर्म वाले कठोर तप, शरीर को अत्यधिक कष्ट देने में विश्वास रखते थे। इसके अतिरिक्त उनका अहिंसा में आवश्यकता से अधिक विश्वास था। जन सामान्य के लिए इन नियमों का पालन करना बहुत कठिन था। चौथा, बौद्ध धर्म के सिद्धांत सरल थे। परिणामस्वरूप लोगों ने जैन धर्म की अपेक्षा बौद्ध धर्म को अपनाना आरंभ कर दिया।
प्रश्न 13.
जैन संघ के बारे में आप क्या जानते हैं ? (What do you know about Jain Sangha ?)
उत्तर-
जैन संघ की स्थापन स्वामी महावीर जी ने की थी। इसमें शामिल होने वाले प्रत्येक भिक्षु तथा भिक्षुणियों को अपने माता-पिता और संरक्षक से आज्ञा लेनी पड़ती थी। उनको बहुत अनुशासित जीवन व्यतीत करना पड़ता था। जैन संघ के सारे सदस्य वर्षा के चार महीनों को छोड़कर बाकी समय अलग-अलग स्थानों पर जाकर धर्म प्रचार करने में व्यतीत करते थे। जैन संघ का मुखिया आचार्य कहलाता था। स्त्रियों के अपने अलग संघ होते थे।
प्रश्न 14.
जैन मत की देन। (Legacy of Jainism.)
अथवा
जैन मत का प्रभाव। (Effects of Jainism.)
उत्तर-
जैन मत ने भारतीय सभ्यता को कई क्षेत्रों में बहुमूल्य देन दी। उन्होंने परस्पर भ्रातृत्व तथा समानता का प्रचार किया। जैन मत ने लोगों को सादा तथा पवित्र जीवन व्यतीत करने के लिए प्रेरित किया। जैन धर्म के विद्वानों ने अनेक भाषाओं में अपने ग्रंथ लिखे। इस कारण क्षेत्रीय भाषाओं को उत्साह मिला। जैनियों ने अनेक प्रभावशाली तथा प्रसिद्ध मंदिरों का निर्माण करवाया। इस कारण भारतीय भवन निर्माण कला को एक नया उत्साह मिला। जैन धर्म ने शांति का संदेश दिया।
प्रश्न 15.
स्वामी पार्श्वनाथ पर एक संक्षिप्त नोट लिखो। (Write a short note on Lord Parshvanatha.)
उत्तर-
स्वामी पार्श्वनाथ का जन्म स्वामी महावीर के जन्म से 250 वर्ष पहले बनारस के राजा अश्वसेन के घर हुआ था। उनकी माता जी का नाम वामादेवी था। उनका बचपन बहुत ही ऐश-ओ-आराम में बीता। 30 वर्षों की आयु में पार्श्वनाथ ने अपने सारे सुखों का त्याग कर दिया और सच्चे ज्ञान की खोज में निकल गये। उनको 83 दिनों के घोर तप के बाद परम ज्ञान प्राप्त हुआ। इसके बाद उन्होंने अपने जीवन के बाकी 70 वर्ष अपने उपदेशों का प्रचार करने में व्यतीत किये। 777 ई० पू० के लगभग उन्होंने बिहार के माऊँट समेता नामक पहाड़ी पर निर्वाण प्राप्त किया। पार्श्वनाथ की शिक्षा को चार्तुयाम अथवा चार प्रण कहते हैं। यह चार प्रण ये हैं—
- सजीव वस्तुओं को कष्ट न पहुँचायें (अहिंसा)।
- झूठ न बोलो (सुनृत)।
- बिना दिये कुछ न लो (अस्तेय)।
- सांसारिक पदार्थों से मोह न करो (अपरिग्रह)।
प्रश्न 16.
स्वामी महावीर पर एक संक्षिप्त नोट लिखें।
(Write a short note on Lord Mahavira.)
अथवा
जैन धर्म के 24वें तीर्थंकर के महत्त्व को दर्शाइए।
(Describe the importance of 24th Tirthankar of Jainism.)
उत्तर-
स्वामी महावीर जैन धर्म के 24वें तीर्थंकर थे। उन्हें जैन धर्म का वास्तविक संस्थापक माना जाता है। उनका जन्म 599 ई० पू० वैशाली के निकट कुंडग्राम में हुआ। उनके पिता जी का नाम सिद्धार्थ तथा माता जी का नाम त्रिशला था। महावीर का बचपन का नाम वर्द्धमान था। वे शुरू से ही बहुत विचारशील थे। वे सांसारिक कार्यों में बहुत कम रुचि लेते थे। महावीर की शादी एक सुंदर राजकुमारी यशोदा से की गई। उनके घर एक पुत्री ने जन्म लिया जिसका नाम प्रियदर्शना अथवा अनोजा रखा गया। महावीर ने 30 वर्षों की आयु में गृह त्याग दिया था। उन्होंने 12 वर्ष तक घोर तपस्या के पश्चात् ज्ञान प्राप्त किया। उन्होंने लोगों में फैले अंधकार को दूर करने के लिए अपने ज्ञान का प्रसार किया। राजगृह, वैशाली, कौशल, मिथला, विदेह तथा अंग उनके प्रसिद्ध प्रचार केंद्र थे। महावीर ने त्रि-रत्न अहिंसा, कठिन तप, शुद्ध आचरण आदि पर बल दिया। वह यज्ञों, बलियों, वेदों, संस्कृत भाषा तथा ईश्वर के अस्तित्व में विश्वास नहीं रखते थे। 527 ई० पू० उन्होंने पावा में निर्वाण प्राप्त किया। निस्संदेह जैन धर्म के विकास में उनका योगदान बहुमूल्य था।
प्रश्न 17.
भगवान महावीर की शिक्षाओं के बारे में चर्चा कीजिए।
(Discuss about the teachings of Lord Mahavira.)
अथवा
स्वामी महावीर की शिक्षाएँ का संक्षिप्त वर्णन करें।
(Discuss briefly the teachings of Lord Mahavira.)
अथवा
जैन धर्म की मुख्य शिक्षाएँ क्या थीं?
(What were the main teachings of Jainism ?)
अथवा
जैन धर्म की प्रमुख शिक्षाओं के बारे में जानकारी दीजिए।
(Describe the pre-eminent teaching of Jainism.)
अथवा
जैन धर्म का आधार उसकी नैतिक कीमतें हैं। संक्षिप्त चर्चा करें।
(The base of Jainism is their Ethical values. Discuss in brief.)
अथवा
जैन धर्म की नैतिक कीमतों के बारे में जानकारी दीजिए।
(Describe the moral-values of Jainism.)
अथवा
नैतिक कीमतें जैन धर्म में प्रमुख हैं। चर्चा कीजिए।
(Moral values are supreme in Jainism. Discuss.)
उत्तर-
स्वामी महावीर जी की शिक्षाएँ अत्यंत सरल एवं प्रभावशाली थीं। उनके अनुसार मानव जीवन का परम उद्देश्य निर्वाण (मुक्ति) प्राप्त करना है। अतः उन्होंने अपने अनुयायियों को तीन रत्नों—
- सच्ची श्रद्धा,
- सच्चा ज्ञान,
- और शुद्ध आचरण पर चलने के लिए कहा।
वे कठोर तप में विश्वास रखते थे। वे अहिंसा पर बहुत ज़ोर देते थे। उनके अनुसार मनुष्य और पशुओं के अतिरिक्त हमें पेड़-पौधों और पक्षियों आदि को भी कष्ट नहीं देना चाहिए। वे आवागमन और कर्म सिद्धांतों में विश्वास रखते थे। उन्होंने समानता व आपसी भाईचारे का प्रचार किया। उन्होंने लोगों को सादा एवं पवित्र जीवन व्यतीत करने की प्रेरणा दी। उन्होंने हिंदू धर्म में फैले झूठे रीति-रिवाजों और यज्ञों का जोरदार शब्दों में खंडन किया। वे वेदों और संस्कृत भाषा की पवित्रता में विश्वास नहीं रखते थे। उन्होंने अपना प्रचार लोगों की साधारण भाषा में किया। वे परमात्मा के अस्तित्व में भी विश्वास नहीं रखते थे। उनका कथन था कि मनुष्य अपने भाग्य का स्वयं निर्माता है। अतः उसे ईश्वर की सहायता की आवश्यकता नहीं है। जैसा मनुष्य कर्म करेगा उसे वैसा ही फल प्राप्त होगा। वे तीर्थंकरों की उपासना में विश्वास रखते थे।

प्रश्न 18.
त्रि-रत्न से क्या भाव है ? इसका क्या महत्त्व है ? (What is meant by Tri-Ratnas ? What is its importance ?)
अथवा
त्रि-रत्न से क्या भाव है ?
(What is meant by Tri-Ratnas ?)
अथवा
आप त्रि-रत्न के बारे में क्या जानते हैं ? (What do you understand by Tri-Ratna ?)
अथवा
जैन धर्म के तीन रत्नों का उल्लेख करें। (Write about the Tri-Ratnas of Jainism.)
उत्तर-
जैन धर्म के अनुसार मनुष्य के जीवन का परम उद्देश्य मोक्ष अथवा निर्वाण प्राप्त करना है। इसको प्राप्त करने के लिए जैन धर्म के अनुसार प्रत्येक व्यक्ति के लिए त्रि-रत्नों पर चलना अति ज़रूरी है। ये तीन रत्न हैंसच्चा विश्वास, सच्चा ज्ञान और सच्चा आचार। पहले रत्न के अनुसार प्रत्येक व्यक्ति को 24 तीर्थंकरों, नौ सच्चाइयों और जैन शास्त्रों में अटल विश्वास होना चाहिए। दूसरे रत्नानुसार जैनियों को सच्चा और पूर्ण ज्ञान प्राप्त करना चाहिए। यह तीर्थंकरों के उपदेशों के गहरे अध्ययन से प्राप्त होता है। इस ज्ञान के दो रूप बताये गये हैं जिनको प्रत्यक्ष और परोक्ष ज्ञान कहा जाता है। आत्मा द्वारा प्राप्त ज्ञान को प्रत्यक्ष ज्ञान कहते हैं और वह ज्ञान जो इंद्रियों के द्वारा प्राप्त होता है उसको परोक्ष ज्ञान कहा जाता है। तीसरे रत्नानुसार प्रत्येक व्यक्ति को सच्चे आचार के अनुसार अपना जीवन व्यतीत करना चाहिए। सच्चा आचार वह है जिसकी शिक्षा जैन धर्म देता है। ये तीनों रत्न साथ-साथ चलते हैं। इनमें से किसी एक की अनुपस्थिति मनुष्य को उसकी मंज़िल तक नहीं पहुँचा सकती। उदाहरण के तौर पर जैसे एक दीये को प्रकाश देने के लिए उसमें तेल, बाती और आग का होना ज़रूरी है। यदि इसमें से एक भी वस्त की कमी हो तो वह प्रकाश नहीं दे सकता।
प्रश्न 19.
जैन धर्म में अहिंसा का क्या महत्त्व है ? (What is the importance Ahimsa in Jainism ?)
अथवा
जैन धर्म में अहिंसा के महत्त्व का वर्णन करें।
(Explain the importance of Ahimsa in Jainism.)
उत्तर-
जैन धर्म में अहिंसा पर बहुत ज़ोर दिया गया है। अहिंसा की महत्ता बताते हुए आचारंग सूत्र में कहा गया है, “सभी को अपना-अपना जीवन प्यारा है, सब ही सुख चाहते हैं, दुःख कोई नहीं चाहता, अधिक कोई नहीं चाहता, सब को जीवन प्यारा है और सारे ही जीने की इच्छा रखते हैं।” इसीलिए जो हमारे लिए सुखमयी है वह दूसरों के लिए भी सुखमयी है। हिंसा दो तरह की होती है-मन से हिंसा और कर्म से हिंसा। कर्म अथवा अमल में आने वाली हिंसा से पहले मन भाव विचारों में हिंसा आती है। गुस्सा, अहंकार, लालच और धोखा मन की हिंसा है। इसलिए हिंसा से बचने के लिए मन के विचारों को शुद्ध करना अति ज़रूरी है। जैन धर्म के अनुसार मनुष्यों के अतिरिक्त पशुओं, पत्थरों .और वृक्षों आदि में भी आत्मा निवास करती है। इसलिए हमें किसी जीव या निर्जीव को कष्ट नहीं देना चाहिए। इसी कारण जैनी लोग नंगे पाँव चलते हैं, मुँह पर पट्टी बाँधते हैं, पानी छान कर पीते हैं और अंधेरा हो जाने के बाद कुछ नहीं खाते ताकि किसी जीव की हत्या न हो जाये।
प्रश्न 20.
जैन धर्म की नौ सच्चाइयों पर नोट लिखो। (Write a short note on the Nine Truths of the Jainism.)
अथवा
जैन धर्म के नौ-तत्त्वों के बारे में जानकारी दें।
(Describe the Nine Tatvas of Jainism.)
उत्तर-
जैन दर्शन नौ सच्चाइयों की शिक्षा देता है। ये सच्चाइयाँ हैं—
- जीव-जैन दर्शन में आत्मा को जीव कहा गया है। यह चेतन सुरूप है। यह शरीर के कर्मों के अच्छे-बुरे फल भुगतता है और आवागमन के चक्र में पड़ता है।
- अजीव-यह जंतु पदार्थ है। यह निर्जीव है और इनमें समझ नहीं होती। इनकी दो श्रेणियाँ हैं रूपी और अरूपी।
- पुण्य-यह अच्छे कर्मों का नतीजा है। इसके नौ साधन हैं।
- पाप-यह जीव के बंधन का मुख्य कारण है। इसके परिणामस्वरूप घोर सजायें मिलती हैं।
- अशर्व-यह वह प्रक्रिया है जिसके अनुसार आत्मा अपने अंदर कर्मों को संचित करती रहती है। कर्म 8 किस्मों के होते हैं।
- संवर-कर्म को आत्मा की ओर आने की क्रिया को रोकने को संवर कहते हैं। कर्म को रोकने की 57 विधियाँ हैं।
- बंध-इससे भाव बंधन है। यह जीव (आत्मा) का पुदगल (परमाणु) से मेल है। बंध के लिए पाँच कारण जिम्मेवार हैं।
- निर्जर-इस से भाव है दूर भगाना। यह कर्मों को नष्ट करने और जल देने का कार्य करता है।
- मोक्ष-इसमें जीव कर्मों के जंजाल से मुक्त हो जाता है। यह पूर्ण शाँति की अवस्था है जिसमें हर तरह के दुःखों से छुटकारा प्राप्त हो जाता है।
प्रश्न 21.
जैन दर्शन में कर्म सिद्धांत का क्या महत्त्व है ? (What is the importance of Karma Theory in Jain Philosophy ?)
अथवा
जैन धर्म का कार्य सिद्धांत के बारे में क्या विचार है ? (What is meant by Karma Theory of Jainism ?)
उत्तर-
जैन दर्शन में कर्म सिद्धांत को एक महत्त्वपूर्ण स्थान प्राप्त है। इस सिद्धांत के अनुसार, “जैसा करोगे वैसा भरोगे, जैसा बीजोगे वैसा काटोगे, यदि कर्म अच्छे होंगे तो अच्छा फल मिलेगा, बुरा करोगे तो बुरा होगा, किसी भी स्थिति में कर्मों से छुटकारा नहीं मिलेगा।” जैसे ही हमारे मन में कोई अच्छा या बुरा विचार आता है वह तुरंत जीव (आत्मा) से उसी तरह जुड़ जाता है, जैसे तेल लगे हुए शरीर से धूलि कण चिपक जाते हैं। ये कर्म आठ प्रकार के हैं-
- ज्ञानवर्णीय कर्म- यह आत्मा के ज्ञान को रोकते हैं।
- दर्शनवीय कर्म- यह आत्मा की इच्छा शक्ति को रोकते हैं।
- वैदनीय कर्म-ये सुख-दुःख उत्पन्न करने वाले कर्म हैं।
- मोहनीय कर्म-ये आत्मा को मोह माया में फंसाने वाले कर्म हैं।
- आयु कर्म-ये कर्म मनुष्य की आयु को निर्धारित करते हैं।
- नाम कर्म-ये कर्म मनुष्य के व्यक्तित्व को निर्धारित करते हैं।
- गोत्र कर्म-ये व्यक्ति के गोत्र और समाज में उसके ऊँचे या नीचे स्थान को निर्धारित करते हैं।
- अंतरीय कर्म-ये अच्छे कर्म को रोकने वाले कर्म हैं।
प्रश्न 22.
जैन धर्म में जीव एवं अजीव से क्या अभिप्राय है ? (What is meant by Jiva and Ajiva in Jainism ?)
अथवा
जैन धर्म में जीव से क्या अभिप्राय है?
(What is meant by Jiva in Jainism ?)
उत्तर-
1. जीव-जीव शब्द का अर्थ है आत्मा। यह चेतन तथ्य है। जैन दर्शन में जीव दो प्रकार के हैं। इनको सांसारिक जीव और मुक्त जीव कहा जाता है। सांसारिक जीव को बंधन जीव भी कहते हैं। यह जीव आवागमन के चक्र में रहता है और अपने कर्मों के अनुसार बार-बार जन्म लेता है और अपने अच्छे बुरे फल भुगतता है। मुक्त जीव वह जीव है जो पुनर्जन्म से रहित है। यह जीव अनंत ज्ञान वाला, अनंत शक्ति वाला और अनंत गुणों वाला होता है। यह जीव कर्मों के जाल से मुक्त होता है।
2. अजीव-अजीव से भाव उन जड़ पदार्थों से है जिनमें चेतना नहीं होती जैसे पुस्तक, कागज़, मेज़ और स्याही आदि। उदाहरण के तौर पर ऊँट के शरीर में जीव फैल कर ऊँट जितना बड़ा हो जाता है और कीड़ी के शरीर में सिकुड़ कर कीड़ी जितना हो जाता है । यह जीव तब नहीं दिखाई देता है परंतु शरीर की क्रियाओं के आधार पर इसकी उपस्थिति का ज्ञान हो जाता है। परंतु जब शरीर का अंत हो जाता है तो जीव लोप हो जाता है। जीव जिस शरीर को धारण करता है वह उस के आकार का ही हो जाता हैं।
प्रश्न 23.
जैन धर्म में पाप एवं पुण्य से क्या अभिप्राय है ? (What is meant by Papa and Punya in Jainism ?)
अथवा
जैन धर्म में पाप से क्या अभिप्राय है ?
(What is meant by Paap in the Jainism ?)
उत्तर-
1. पाप-पाप को जीव के बंधन का मुख्य कारण माना जाता है। जीवों को मारना, झूठ, चोरी, क्रोध, लोभ, मोह, अहंकार, धोखा, नशा और दुश्मनी आदि सब पापों के भार में वृद्धि करते हैं। पापियों को घोर सजायें मिलती हैं। आपने देखा होगा कि एक ही घर में पैदा हुए दो सगे भाइयों के जीवन में भारी अंतर होता है। एक ऊँची पदवी पर सुशोभित होता है और उसको प्रसिद्धि प्राप्त होती है। दूसरा दर-दर की ठोकरें खाता फिरता है, चोरियाँ करता है और बदनामी कमाता है। ऐसा क्यों होता है ? जैन दर्शन के अनुसार ऐसा व्यक्ति के पुण्य और पाप कमाने का कारण होता है। पापी मनुष्य कभी भी सुखी नहीं हो सकता और उसको अपने जीवन में घोर संकट का सामना करना पड़ता है। ऐसे व्यक्ति की आत्मा भी तड़पती रहती है। जैन सूत्रों के अनुसार पापों के 82 अलगअलग परिणाम निकलते हैं।
2. पुण्य-पुण्य वह कर्म है जो अच्छे अमलों से कमाये जाते हैं। पुण्य कमाने के अलग-अलग ढंग हैं। भूखे को खाना देना, प्यासे को पानी पिलाना, नंगे को कपड़ा देना, हाथों से सेवा करनी, मीठा बोलना आदि पुण्य के काम हैं, पुण्य को मानने के 42 साधन हैं। अच्छी सेहत, आर्थिक समृद्धि, प्रसिद्धि, अच्छा वैवाहिक जीवन, अच्छे रिश्तेदारों और दोस्तों का मिलना, अच्छी पढ़ाई और उच्च पदवियों पर नियुक्ति आदि अच्छे पुण्यों का ही नतीजा है। पुण्य को आत्मा का सहायक माना जाता है क्योंकि इससे खुशी प्राप्त होती है।
प्रश्न 24.
महावीर जी की शिक्षाओं का साधारण मनुष्य के जीवन के लिए क्या महत्त्व था ? (What was the importance of Mahavira’s teachings in the life of a common man ?)
उत्तर-
महावीर जी की शिक्षाएँ साधारण मनुष्य के लिए महत्त्वपूर्ण थीं। उस समय हिंदू धर्म में जाति प्रथा बहुत कठोर हो गई थी। उच्च जाति के लोग निम्न जाति के लोगों से घृणा करते थे। भगवान महावीर ने अपने धर्म में _बिना किसी भेद-भाव के प्रत्येक वर्ग के लोगों को शामिल किया। इससे समाज में प्रचलित परस्पर घृणा बहुत सीमा तक दूर हुई और लोगों में परस्पर बंधुत्व एवं प्रेम-भाव बढ़ गया। महावीर जो ने समाज में प्रचलित अंध-विश्वासों का जोरदार शब्दों में खंडन किया। साधारण लोग भी इन परंपराओं के विरुद्ध थे। इसलिए उनके हृदयों पर महावीर जी की शिक्षाओं का गहरा प्रभाव पड़ा। महावीर जी की अहिंसा नीति के कारण लोगों को युद्ध से घृणा हो गई और वे शाँति को पसंद करने लगा। महावीर जी ने लोगों को समाज सेवा का उपदेश दिया। परिणामस्वरूप जैन मत वालों ने लोगों की सहायता के लिए बहुत-सी धर्मशालाएँ बनवाईं। शिक्षा प्रचार के लिए शिक्षा संस्थाएँ और मनुष्यों एवं पशुओं की चिकित्सा के लिए अस्पताल खोले।
प्रश्न 25.
महावीर की शिक्षा के अनुसार एक जैन भिक्षु को कैसा जीवन व्यतीत करना पड़ता था ?
(What type of life a Jain monk had to lead according to the teachings of Mahavira ?)
उत्तर-
महावीर की शिक्षा के अनुसार जैन भिक्षुओं को बहुत स्वच्छ जीवन व्यतीत करना पड़ता था। प्रत्येक भिक्षु को पाँच प्रतिज्ञाओं की पालना करनी पड़ती थी।
- प्रत्येक भिक्षु को सदैव सत्य बोलना चाहिए।
- उसको अहिंसा की नीति पर चलना चाहिए।
- उसको कोई भी ऐसी वस्तु अपने पास नहीं रखनी चाहिए जो उसको दान में प्राप्त न हुई हो।
- उसको अपने पास धन नहीं रखना चाहिए।
- उसको ब्रह्मचर्य का पालन करना चाहिए।
इनके अतिरिक्त भिक्षु के लिए आवश्यक था कि उनकी वेश-भूषा और खाना-पीना बिल्कुल सादा हो। उनके लिए छाता और सुगंध देने वाली वस्तुओं के प्रयोग करने पर प्रतिबंध था। भिक्षु के लिए किसी स्त्री से बातचीत करने पर भी प्रतिबंध था। उनको सदैव मीठे वचन बोलने के लिए कहा गया था जिससे किसी को दुःख न पहुँचे। उनको इस बात का भी ध्यान रखना पड़ता था कि उनके चलने से या खान-पीने में किसी जीव की हत्या न हो।
प्रश्न 26.
दिगंबर और श्वेतांबर पर एक नोट लिखें। (Write a note on Digambara and Svetambara.)
अथवा
दिगंबर तथा श्वेतांबर से आपका क्या अभिप्राय है ? (What do you understand by Digambara and Svetambara ?)
उत्तर-
जैन धर्म के सभी संप्रदायों में से दिगंबर तथा श्वेतांबर संप्रदायों को प्रमुख स्थान प्राप्त है। दिगंबर से अभिप्राय था नग्न रहने वाले तथा श्वेतांबर से अभिप्राय था श्वेत (सफ़ेद) वस्त्र धारण करने वाले। इन दोनों संप्रदायों में प्रमुख अंतर निम्नलिखित अनुसार थे—
- दिगंबर संप्रदाय के अनुयायी नग्न रहते हैं जबकि श्वेतांबर संप्रदाय के अनुयायी सफ़ेद वस्त्र धारण करते हैं।
- दिगंबर संप्रदाय स्त्रियों को जैन संघ में सम्मिलित होने की आज्ञा नहीं देता जबकि श्वेतांबर संप्रदाय वाले ऐसा कोई प्रतिबंध नहीं लगाते।
- दिगंबर संप्रदाय वालों का कहना है कि स्त्रियां तब एक मोक्ष प्राप्त नहीं कर सकती जब तक वे पुरुष के रूप में जन्म नहीं लेतीं। श्वेतांबर संप्रदाय वाले इस सिद्धांत को गलत मानते हैं। उनका कथन है कि स्त्रियाँ इसी जन्म में मोक्ष प्राप्त कर सकती हैं।
- दिगंबर संप्रदाय वालों का यह कथन है कि स्वामी महावीर जी ने विवाह नहीं करवाया था। श्वेतांबर संप्रदाय वालों का यह कथन है कि स्वामी महावीर जी ने विवाह करवाया था तथा उनकी एक पुत्री थी जिसका नाम प्रियदर्शना था।
- दिगंबर संप्रदाय वालों का कथन है कि ज्ञान प्राप्त करने वाले साधुओं को भोजन की आवश्यकता नहीं रहती जबकि श्वेतांबर संप्रदाय वाले इस बात का खंडन करते हैं।
- दिगंबर तथा श्वेतांबर संप्रदायों का साहित्य भी अलग-अलग है।
- दिगंबर संप्रदाय वालों की मूर्तियाँ नंगेज हैं जबकि श्वेतांबर संप्रदाय वालों की मूर्तियों को वस्त्र पहनाए जाते हैं तथा उन्हें गहनों से सुसज्जित किया जाता है।

प्रश्न 27.
जैन धर्म भारत में लोकप्रिय क्यों नहीं हो सका ? (Why could not Jainism become popular in India ?)
उत्तर-
जैन धर्म की शिक्षाएँ यद्यपि सरल थीं, परंतु कई कारणों से यह धर्म लोगों में लोकप्रिय न हो सका। पहला, जैन धर्म वालों ने अपने धर्म के प्रचार के लिए कोई विशेष प्रयत्न नहीं किया। किसी भी धर्म की सफलता के लिए ऐसा किया जाना आवश्यक होता है। दूसरा, जैन धर्म को बौद्ध धर्म की भाँति राजकीय संरक्षण प्राप्त नहीं हो सका। यह सही है कि बिंबिसार, अजातशत्रु और खारवेल जैसे शासकों ने जैन धर्म को अपना संरक्षण दिया, परंतु वे बौद्ध धर्म की भाँति जैन धर्म को प्रगति के शिखर तक पहुँचाने में विफल रहे। तीसरा, जैन धर्म वाले कठोर तप, शरीर को अत्यधिक कष्ट देने में विश्वास रखते थे। इसके अतिरिक्त उनका अहिंसा में आवश्यकता से अधिक विश्वास था। वे मुँह पर पट्टी बाँधते थे, नंगे पाँव चलते थे और पानी छान कर पीते थे ताकि किसी जीव की मृत्यु न हो जाए। वे वृक्षों और पत्थरों को भी प्राणवान् मानते थे। इसलिए इन्हें कष्ट देना भी पाप समझा जाता था। वे बीमार पड़ने पर औषधि का भी प्रयोग नहीं करते थे। जन सामान्य के लिए इन नियमों का पालन करना बहुत कठिन था। चौथा, जैन धर्म के लोकप्रिय न होने का एक कारण यह भी था कि उस समय बौद्ध धर्म के सिद्धांत भी बहुत सरल थे। परिणामस्वरूप लोगों ने जैन धर्म की अपेक्षा बौद्ध धर्म को अपनाना आरंभ कर दिया। पाँचवां, समय के साथ-साथ जैन लोगों ने हिंदू धर्म के कई सिद्धांतों को अपना लिया। परिणामस्वरूप वे अपने अलग अस्तित्व को न बनाए रख सके।
प्रश्न 28.
जैन स्रोत। (The Jaina Sources.)
उत्तर-
जैन स्रोत प्राचीन भारत के इतिहास पर महत्त्वपूर्ण प्रकाश डालते हैं। जैनियों ने अनेक ग्रंथों की रचना की। ये ग्रंथ प्राकृत अथवा अर्द्ध मगधी जो उस समय लोगों की बोलचाल की आम भाषा थी में लिखे गए हैं। जैनियों के धार्मिक ग्रंथों में 12 अंशों को सबसे महत्त्वपूर्ण एवं पवित्र समझ जाता है। इनमें महावीर के जीवन तथा जैन धर्म के सिद्धांतों पर प्रकाश डाला गया है। जैन धर्म के 12 उपांग भी हैं। इनमें अधिकाँश मिथिहासिक कथाओं का वर्णन मिलता है। जैन धर्म के 10 प्राकिरणों से महावीर के जीवन एवं उसके उपदेशों संबंधी महत्त्वपूर्ण जानकारी प्राप्त होती है। 6 छेदसूत्रों में जैन भिक्षु एवं भिक्षुणियों के नियमों का वर्णन किया गया है। जैनी साहित्य में 4 मूलसूत्रों को बहुमूल्य समझा जाता है। इनसे जैन धर्म से संबंधित कथाओं के बारे में महत्त्वपूर्ण जानकारी उपलब्ध होती है।
प्रश्न 29.
जैन मत की भारतीय सभ्यता को क्या देन है ? (What is the legacy of Jainism to the Indian Civilization ?)
उत्तर-
जैन मत ने भारतीय सभ्यता को कई क्षेत्रों में बहुमूल्य देन दी। महावीर ने जाति प्रथा का जोरदार शब्दों में खंडन किया। उन्होंने अपने धर्म में प्रत्येक जाति से संबंधित लोगों को शामिल किया। उन्होंने परस्पर भ्रातृत्व तथा समानता का प्रचार किया। परिणामस्वरूप समाज में फैली घृणा को काफ़ी सीमा तक दूर किया जा सका। जैन मत ने लोगों को सादा तथा पवित्र जीवन व्यतीत करने के लिए प्रेरित किया। इसके प्रयत्नों के कारण लोगों में फैले बहुत-से धार्मिक अंध-विश्वासों का अंत हो गया। जैन धर्म की बढ़ती हुई प्रसिद्धि को देख कर हिंदू धर्म के नेताओं ने इसमें आवश्यक सुधार किए। जैन धर्म के विद्वानों ने अनेक भाषाओं में अपने ग्रंथ लिखे। इस कारण क्षेत्रीय भाषाओं को उत्साह मिला। ये ग्रंथ भारतीय इतिहास के बहुमूल्य स्रोत हैं। जैनियों ने अनेक प्रभावशाली तथा प्रसिद्ध मंदिरों का निर्माण करवाया। इस कारण भारतीय भवन निर्माण कला को एक नया उत्साह मिला। जैन धर्म ने लोगों के कल्याण के लिए अनेक धर्मशालाएँ, शौक्षिक संस्थाएँ तथा अस्पतालों आदि की स्थापना की जो आज भी जारी हैं। जैन धर्म ने शाँति का संदेश दिया। यह युद्धों के विरुद्ध था। इसका भारतीय राजनीति पर बुरा प्रभाव पड़ा।
वस्तुनिष्ठ प्रश्न
प्रश्न 1. ‘जैन’ शब्द से क्या अभिप्राय है ?
उत्तर-विजेता।
प्रश्न 2. जैन धर्म को आरंभ में क्या नाम दिया गया था ?
उत्तर-निग्रंथ।
प्रश्न 3. निग्रंथ से क्या अभिप्राय है ?
उत्तर-बंधनों से मुक्त।
प्रश्न 4. जैन आचार्यों को किस अन्य नाम से जाना जाता था ?
उत्तर-तीर्थंकर।
प्रश्न 5. तीर्थंकर से क्या अभिप्राय है ?
उत्तर-संसार के भवसागर से पार कराने वाला गुरु।
प्रश्न 6. जैन धर्म में कुल कितने तीर्थंकर हुए हैं ?
उत्तर-24 तीर्थंकर।।
प्रश्न 7. जैन धर्म के प्रथम तीर्थंकर का क्या नाम था ?
अथवा
जैन धर्म के पहले तीर्थंकर का नाम बताओ।
उत्तर-ऋषभदेव।
प्रश्न 8. जैन धर्म के 23वें तीर्थंकर कौन थे ?
उत्तर-पार्श्वनाथ।
प्रश्न 9. स्वामी पार्श्वनाथ जैन धर्म के कौन-से तीर्थंकर थे ?
उत्तर-23वें।
प्रश्न 10. स्वामी पार्श्वनाथ का जन्म कहाँ हुआ था ?
उत्तर-बनारस में।
प्रश्न 11. स्वामी पार्श्वनाथ के पिता जी कौन थे ?
उत्तर- बनारस के राजा अश्वसेन।
प्रश्न 12. स्वामी पार्श्वनाथ ने जब अपना घर त्याग दिया उस समय उनकी आयु कितनी थी ?
उत्तर-30 वर्ष।
प्रश्न 13. स्वामी पार्श्वनाथ ने कितने दिनों के घोर तप के बाद परम ज्ञान प्राप्त किया ?
उत्तर-83 दिनों के।
प्रश्न 14. स्वामी पार्श्वनाथ ने कितने सिद्धांतों का प्रचलन किया ?
उत्तर-स्वामी पार्श्वनाथ ने चार सिद्धांतों का प्रचलन किया।
प्रश्न 15. स्वामी पार्श्वनाथ के सिद्धांतों को क्या कहा जाता है ?
उत्तर-चातुर्याम।
प्रश्न 16. स्वामी पार्श्वनाथ का कोई एक सिद्धांत बताएँ।
उत्तर-कभी झूठ न बोलो।
प्रश्न 17. स्वामी पार्श्वनाथ ने कितने वर्ष प्रचार किया ?
उत्तर-स्वामी पार्श्वनाथ ने 70 वर्ष प्रचार किया।
प्रश्न 18. स्वामी पार्श्वनाथ ने कब निर्वाण प्राप्त किया?
उत्तर-777 ई० पू०।
प्रश्न 19. जैन धर्म का संस्थापक कौन था और वह कितना तीर्थंकर था ?
उत्तर-जैन धर्म का संस्थापक स्वामी महावीर था और वह 24वां तीर्थंकर था।
प्रश्न 20. जैन धर्म का अंतिम तीर्थंकर कौन था ?
अथवा
जैन धर्म का 24वां तीर्थंकर कौन था ?
उत्तर-स्वामी महावीर जी।

प्रश्न 21. जैन धर्म के पहले व आखिरी तीर्थंकर का नाम बताएँ।
उत्तर-जैन धर्म के पहले तीर्थंकर का नाम ऋषभदेव था तथा आखिरी तीर्थंकर का नाम स्वामी महावीर था।
प्रश्न 22. स्वामी महावीर जी का जन्म कब और कहाँ हुआ ?
उत्तर-599 ई० पू० कुंडग्राम में।
प्रश्न 23. स्वामी महावीर जी का जन्म कहाँ हुआ ?
उत्तर-कुंडग्राम में।
प्रश्न 24. स्वामी महावीर जी के पिता जी का क्या नाम था ?
उत्तर-सिद्धार्थ।
प्रश्न 25. स्वामी महावीर जी की माता जी का क्या नाम था ?
उत्तर-त्रिशला।
प्रश्न 26. भगवान् महावीर जी के जन्म से पूर्व उनकी माता को कितने स्वप्न आए थे ?
उत्तर-14.
प्रश्न 27. स्वामी महावीर जी का आरंभिक नाम क्या था ?
उत्तर-वर्धमान।
प्रश्न 28. स्वामी महावीर जी का संबंध किस कबीले के साथ था ?
उत्तर-जनत्रिका।
प्रश्न 29. स्वामी महावीर जी का विवाह किसके साथ हुआ ?
उत्तर-यशोदा से।
प्रश्न 30. स्वामी महावीर जी की पुत्री का क्या नाम था ?
उत्तर-प्रियदर्शना।
प्रश्न 31. घर त्याग के समय स्वामी महावीर जी की आयु कितनी थी?
उत्तर-30 वर्ष।
प्रश्न 32. स्वामी महावीर जी ने कितने वर्षों तक कठोर तप किया ?
उत्तर-12 वर्ष।
प्रश्न 33. स्वामी महावीर जी ने कौन-सी आयु में ज्ञान प्राप्त किया ?
उत्तर-42 वर्ष की।
प्रश्न 34. कैवल्य ज्ञान से क्या भाव है ?
उत्तर-सर्वोच्च सत्य।
प्रश्न 35. स्वामी महावीर जी ने कितने वर्षों तक प्रचार किया ?
उत्तर-30 वर्ष।
प्रश्न 36. स्वामी महावीर जी के कोई दो प्रसिद्ध प्रचार केंद्रों के नाम लिखो।
उत्तर-
- राजगृह
- वैशाली।
प्रश्न 37. स्वामी महावीर जी ने कब निर्वाण प्राप्त किया?
उत्तर-527 ई० पू०।
प्रश्न 38. स्वामी महावीर जी ने कहाँ निर्वाण प्राप्त किया था ?
उत्तर-पावा में।
प्रश्न 39. स्वामी महावीर जी ने जब निर्वाण प्राप्त किया तब उनकी आयु क्या थी ?
उत्तर-72 वर्ष।
प्रश्न 40. जैन धर्म की बुनियादी कीमतें किसने निर्धारित की ?
उत्तर-स्वामी महाबीर जी ने।
प्रश्न 41. जैन धर्म की कोई एक प्रमुख शिक्षा बताएँ।
उत्तर-जैन धर्म अहिंसा में विश्वास रखता था।
प्रश्न 42. त्रिरत्न किस धर्म के साथ संबंधित है ?
उत्तर-जैन धर्म के साथ।
प्रश्न 43. जैन धर्म के तीन रत्न कौन-से हैं ?
अथवा
जैन धर्म के त्रिरत्नों के नाम बताएँ।
अथवा
जैन धर्म के तीन रत्न क्या हैं ?
उत्तर-
- सत्य-श्रद्धा
- सत्य-ज्ञान
- सत्य-आचरण।
प्रश्न 44. जैन धर्म में ब्रह्मचर्य का सिद्धांत किसने प्रचलित किया ?
उत्तर-स्वामी महावीर जी ने।
प्रश्न 45. जैन धर्म दर्शन में कितने तत्त्व माने गए हैं ?
उत्तर-9.
प्रश्न 46. जैन धर्म की कोई दो सच्चाइयाँ बताएँ।
उत्तर-
- पाप
- पुण्य।
प्रश्न 47. जैन दर्शन में आत्मा को क्या कहा गया है ?
उत्तर-जीव।
प्रश्न 48. जैन दर्शन में अजीव की कौन-सी दो श्रेणियाँ हैं ?
उत्तर-
- रूपी
- अरूपी
प्रश्न 49. जैन दर्शन में कर्म को आत्मा की ओर आने की क्रिया को रोकने को क्या कहते हैं ?
उत्तर-संवर।
प्रश्न 50. जैन धर्म में अशर्व के क्या अर्थ है ?
उत्तर-वह प्रक्रिया जिसके अनुसार आत्मा अपने अंदर कर्मों को संचित करती रहती है।
प्रश्न 51. जैन धर्म में पुदगल से क्या अभिप्राय है ?
उत्तर-परमाणु।

प्रश्न 52. जैन धर्म के अनुसार कर्म कितनी प्रकार के हैं ?
उत्तर-8 प्रकार के।
प्रश्न 53. जैन धर्म के किसी एक प्रकार के कर्म का नाम बताएँ।
उत्तर-ज्ञानवर्णनीय कर्म।
प्रश्न 54. जैन धर्म में जीव से क्या भाव है ?
उत्तर-आत्मा।
प्रश्न 55. जैन धर्म में अजीव से क्या भाव है ?
उत्तर-जड़ पदार्थ।
प्रश्न 56. जैन दर्शन में कितनी प्रकार की हिंसा का वर्णन मिलता है ?
उत्तर-108 प्रकार की।
प्रश्न 57. जैन दर्शन में पुण्य को मानने के कितने साधन हैं ?
उत्तर-42.
प्रश्न 58. जैन दर्शन के अनुसार पाप के कितनी प्रकार के परिणाम निकलते हैं ?
उत्तर-82 प्रकार के।
प्रश्न 59. अनेकांतवाद का सिद्धांत किस धर्म के साथ संबंधित है ?
उत्तर-जैन धर्म के साथ।
प्रश्न 60. जैन दर्शन के अनुसार मनुष्य को अपने जीवन में कितने अणुव्रतों की पालना करनी चाहिए ?
उत्तर-पाँच अणुव्रतों की।
प्रश्न 61. जैन धर्म में निर्वाण से क्या अभिप्राय है ?
उत्तर-आवागमन के चक्र से मुक्ति।
प्रश्न 62. जैन धर्म को नास्तिक धर्म क्यों कहा जाता है ?
उत्तर-क्योंकि यह धर्म ईश्वर के अस्तित्व में विश्वास नहीं रखता।
प्रश्न 63. अजीविक संप्रदाय का संस्थापक कौन था ?
उत्तर-गौशाल।
प्रश्न 64. अजीविक संप्रदाय का प्रमुख सिद्धांत क्या था ?
उत्तर-इस संप्रदाय का प्रमुख सिद्धांत नियति (किस्मत) था।
प्रश्न 65. जैन धर्म के दो प्रमुख संप्रदाय कौन-से हैं ?
उत्तर-जैन धर्म के दो प्रमुख संप्रदायों के नाम दिगंबर एवं श्वेतांबर है।
प्रश्न 66. दिगंबर से क्या अभिप्राय है ?
उत्तर-दिगंबर से अभिप्राय है नग्न रहने वाला।
प्रश्न 67. श्वेतांबर से क्या अभिप्राय है ?
उत्तर-श्वेतांबर से अभिप्राय है श्वेत वस्त्र धारण करने वाला।
प्रश्न 68. लोंक सा कौन था ?
उत्तर-लोक सा लोंक संप्रदाय का मुखिया था।
प्रश्न 69. स्थानकवासी संप्रदाय का संस्थापक कौन था ?
उत्तर-वीराजी।
प्रश्न 70. तेरा पंथ का संस्थापक कौन था ?
उत्तर-भीखनजी।
प्रश्न 71. जैन संघ में कितनी तरह के लोग शामिल होते हैं ?
उत्तर-चार तरह के।
प्रश्न 72. जैन संघ में किन्हें सम्मिलित होने की आज्ञा नहीं थी ?
उत्तर- अधर्मी व्यक्तियों को।
प्रश्न 73. जैन धर्म में सम्मिलित होने वाले स्त्री एवं पुरुषों को क्या कहा जाता था ?
उत्तर-
- भिक्षुणियाँ
- भिक्षु।
प्रश्न 74. जैन धर्म ग्रंथों की भाषा क्या है ?
उत्तर-प्राकृत अथवा अर्ध मगधी।
प्रश्न 75. जैन धर्म में सर्वाधिक पवित्र पुस्तकें कौन-सी हैं ?
उत्तर-12 अंग।
प्रश्न 76. जैन धर्म के किसी एक अंग का नाम बताएँ।
उत्तर-आचारांग सूत्र।
प्रश्न 77. जैन धर्म के किस ग्रंथ में जैन भिक्षुओं से संबंधित नियम दिए गए हैं ?
उत्तर-आचारांग सूत्र में।
प्रश्न 78. जैन धर्म में कितने उपांग हैं ?
उत्तर-12 उपांग।
प्रश्न 79. कल्पसूत्र की रचना किसने की थी ?
उत्तर-भद्रबाहू ने।
प्रश्न 80. कल्पसूत्र का विषय क्या है ?
उत्तर-स्वामी महावीर जी का जीवन।
प्रश्न 81. जैन धर्म में कितने छेदसूत्र हैं ?
उत्तर-जैन धर्म में 6 छेदसूत्र हैं।
प्रश्न 82. जैन धर्म से संबंधित मूलसूत्र कितने हैं ?
उत्तर-4.
प्रश्न 83. जैन धर्म के दिगंबर से संबंधित कितनी पुस्तकें उपलब्ध हैं ?
उत्तर-4.
प्रश्न 84. दिगंबर संप्रदाय से संबंधित एक पुस्तक का नाम बताएँ।
उत्तर-पर्थमानु योग।
नोट-रिक्त स्थानों की पूर्ति करें—
प्रश्न 1. जैन धर्म को आरंभ में ………….. के नाम से जाना जाता था।
उत्तर-निग्रंथ
प्रश्न 2. जैन धर्म में कुल ………. तीर्थंकर थे।।
उत्तर-24
प्रश्न 3. जैन धर्म के पहले तीर्थंकर का नाम ………… था।
उत्तर-ऋषभनाथ
प्रश्न 4. जैन धर्म के 23वें तीर्थंकर …………… थे।
उत्तर- पार्श्वनाथ
प्रश्न 5. जैन धर्म के 24वें तीर्थंकर …………… थे।
उत्तर-स्वामी महावीर
प्रश्न 6. स्वामी महावीर का जन्म ……….. में हुआ।
उत्तर-599 ई०पू०
प्रश्न 7. स्वामी महावीर की माता जी का नाम ………. था।
उत्तर-त्रिशला
प्रश्न 8. स्वामी महावीर के जन्म से पहले उनकी माता जी को ………… स्वप्न आए थे।
उत्तर-14
प्रश्न 9. स्वामी महावीर जी की पुत्री का नाम ………. था।
उत्तर-प्रियदर्शना
प्रश्न 10. ज्ञान प्राप्ति के समय स्वामी महावीर जी की आयु ………. थी।
उत्तर-42 वर्ष
प्रश्न 11. स्वामी महावीर जी ने ………. में निर्वाण प्राप्त किया।
उत्तर-527 ई० पू०
प्रश्न 12. जैन धर्म ……….. रत्नों में विश्वास रखता है।
उत्तर-तीन
प्रश्न 13. जैन धर्म में ब्रह्मचर्य का सिद्धांत ………. ने प्रचलित किया।
उत्तर-स्वामी महावीर
प्रश्न 14. जैन धर्म ………… सच्चाइयों में विश्वास रखता है।
उत्तर-नौ

प्रश्न 15. जैन धर्म के अनुसार ………. वह प्रक्रिया है जिसके अनुसार आत्मा अपने आंतरिक कर्मों को संचित करती रहती है।
उत्तर-अशर्व
प्रश्न 16. जैन धर्म ………. प्रकार के कर्मों में विश्वास रखता है।
उत्तर-आठ
प्रश्न 17. अनेकांतवाद को ………… के नाम से भी जाना जाता है।
उत्तर-स्यादवाद
प्रश्न 18. जैन धर्म ………… महाव्रतों में विश्वास रखता है।
उत्तर-पाँच
प्रश्न 19. जैन धर्म के अनुसार मनुष्य के जीवन का सर्वोच्च उद्वेश्य …………. प्राप्त करना है।
उत्तर-निर्वाण
प्रश्न 20. जैन धर्म के अनुसार पुदगल से भाव ……….. है।
उत्तर-परमाणु
प्रश्न 21. अजीविक संप्रदाय का संस्थापक ………… था।
उत्तर-गौशाल
प्रश्न 22. अजीविक संप्रदाय ……….. के सिद्धांत में विश्वास रखता था।
उत्तर-नियति
प्रश्न 23. ………. संप्रदाय वाले श्वेत वस्त्र धारण करते थे।
उत्तर-श्वेतांबर
प्रश्न 24. लोक संप्रदाय का संस्थापक ………. था।
उत्तर-लोक सा
प्रश्न 25. तेरा पंथ संप्रदाय का संस्थापक ……….. था।
उत्तर-भीखनजी
प्रश्न 26. जैन धर्म का संस्थापक ……….. कहलाता था।
उत्तर-आचार्य
प्रश्न 27. जैन धर्म ………… अंगों में विश्वास रखता है।
उत्तर-12
नोट-निम्नलिखित में से ठीक अथवा ग़लत चुनें—
प्रश्न 1. जैन धर्म कुल 20 तीर्थंकरों में विश्वास रखता है।
उत्तर-ग़लत
प्रश्न 2. जैन धर्म के पहले तीर्थंकर का नाम विमल था।
उत्तर-ग़लत
प्रश्न 3. स्वामी पार्श्वनाथ जैन धर्म के 23वें तीर्थंकर थे।
उत्तर-ठीक
प्रश्न 4. स्वामी पार्श्वनाथ को 23 दिनों के कठिन तप के पश्चात् ज्ञान प्राप्त हुआ था।
उत्तर-ग़लत
प्रश्न 5. स्वामी पार्श्वनाथ की शिक्षा को चातुरयाम कहते हैं।
उत्तर-ठीक
प्रश्न 6. स्वामी महावीर जैन धर्म के 24वें तीर्थंकर थे।
उत्तर-ठीक
प्रश्न 7. स्वामी महावीर का जन्म 567 ई०पू० में हुआ था।
उत्तर-ग़लत
प्रश्न 8. स्वामी महावीर जी के बचपन का नाम वर्धमान था।
उत्तर-ठीक
प्रश्न 9. स्वामी महावीर जी की माता का नाम महामाया था।
उत्तर-ग़लत
प्रश्न 10. ज्ञान प्राप्ति के समय स्वामी महावीर जी की उनकी आयु 42 वर्ष थी।
उत्तर-ठीक
प्रश्न 11. स्वामी महावीर जी ने पावा में निर्वाण प्राप्त किया था।
उत्तर-ठीक
प्रश्न 12. जैन धर्म त्रि-रत्नों में विश्वास रखता है।
उत्तर-ठीक
प्रश्न 13. जैन धर्म अहिंसा में विश्वास नहीं रखता है।
उत्तर-ग़लत
प्रश्न 14. जैन धर्म के अनुसार तत्व नौ प्रकार के हैं।
उत्तर-ठीक
प्रश्न 15. जैन धर्म तीन प्रकार के कर्मों में विश्वास रखता है।
उत्तर-ग़लत
प्रश्न 16. जैन धर्म के अनुसार मनुष्य को अपने जीवन में पाँच अनुव्रतों की पालना करनी चाहिए।
उत्तर-ठीक

प्रश्न 17. जैन धर्म के अनुसार मानवीय जीवन का मुख्य उद्देश्य निर्वाण प्राप्त करना है।
उत्तर-ठीक
प्रश्न 18. जैन धर्म के अनुसार सच्चा विश्वास सच्चे ज्ञान की आधारशिला है।
उत्तर-ठीक
प्रश्न 19. जैन धर्म के अनुसार ज्ञान पाँच प्रकार का होता है।
उत्तर-ठीक
प्रश्न 20. जैन धर्म के अनुसार हिंसा आठ प्रकार की होती है।
उत्तर-ग़लत
प्रश्न 21. जैन धर्म में जीव शब्द का अर्थ है ‘आत्मा’।
उत्तर-ठीक
प्रश्न 22. जैन धर्म के अनुसार पुण्य प्राप्त करने के 42 साधन हैं।
उत्तर-ठीक
प्रश्न 23. जैन धर्म के अनुसार कर्म को रोकने की 57 विधियां हैं। .
उत्तर-ठीक
प्रश्न 24. जैन धर्म चार महाव्रतों में विश्वास रखता है।
उत्तर-ग़लत
प्रश्न 25. अजीविक संप्रदाय किस्मत के सिद्धांत में विश्वास रखता है।
उत्तर-ठीक
प्रश्न 26. तारना संप्रदाय का संस्थापक भीखनजी था।
उत्तर-ग़लत
प्रश्न 27. स्थानकवासी संप्रदाय का संस्थापक वीराजी था।
उत्तर-ठीक
प्रश्न 28. जैनियों के धार्मिक ग्रंथों में 12 अंगों को सबसे महत्त्वपूर्ण माना जाता है।
उत्तर-ठीक
नोट-निम्नलिखित में से ठीक उत्तर चनें—
प्रश्न 1.
जैन धर्म कुल कितने तीर्थंकरों में विश्वास रखता है ?
(i) 20
(ii) 23
(iii) 24
(iv) 25
उत्तर-
(iii) 24
प्रश्न 2.
जैन धर्म का पहला तीर्थंकर कौन था ?
(i) पार्श्वनाथ
(ii) महावीर
(iii) विमल
(iv) ऋषभनाथ।
उत्तर-
(iv) ऋषभनाथ।
प्रश्न 3.
जैन धर्म के 23वें तीर्थंकर कौन थे ?
(i) विमल
(ii) अनंत
(iii) ऋषभनाथ
(iv) पार्श्वनाथ।
उत्तर-
(iv) पार्श्वनाथ।
प्रश्न 4.
जैन धर्म के 24वें तीर्थंकर कौन थे ?
(i) अभिनंदन
(ii) महावीर
(iii) पुष्पदंत
(iv) अजित।
उत्तर-
(ii) महावीर
प्रश्न 5.
स्वामी महावीर जी का जन्म कब हुआ ?
(i) 566 ई० पू०
(ii) 567 ई० पू०
(iii) 569 ई० पू०
(iv) 599 ई० पू०।
उत्तर-
(iv) 599 ई० पू०।
प्रश्न 6.
स्वामी महावीर जी का जन्म कहाँ हुआ ?
(i) लुंबिनी में
(ii) कुंडग्राम में
(iii) कुशीनगर में
(iv) कपिलवस्तु में।
उत्तर-
(ii) कुंडग्राम में

प्रश्न 7.
स्वामी महावीर जी के पिता जी का नाम क्या था ?
(i) सिद्धार्थ
(ii) राहुल
(iii) वर्धमान
(iv) इनमें से कोई नहीं।
उत्तर-
(i) सिद्धार्थ
प्रश्न 8.
स्वामी महावीर जी की माता जी का नाम क्या था ?
(i) त्रिशला
(ii) यशोधरा
(iii) महामाया
(iv) प्रजापति गौतमी।
उत्तर-
(i) त्रिशला
प्रश्न 9.
स्वामी महावीर जी के जन्म से पूर्व उनकी माता जी को कितने स्वप्न आए थे ?
(i) 8
(ii) 10
(iii) 12
(iv) 14.
उत्तर-
(iv) 14.
प्रश्न 10.
स्वामी महावीर जी के बचपन का नाम क्या था ?
(i) वर्धमान
(ii) सिद्धार्थ
(ii) राहुल
(iv) इनमें से कोई नहीं।
उत्तर-
(i) वर्धमान
प्रश्न 11.
स्वामी महावीर जी की ज्ञान प्राप्ति के समय उनकी आयु कितनी थी ?
(i) 20 वर्ष
(ii) 30 वर्ष
(iii) 35 वर्ष
(iv) 42 वर्ष।
उत्तर-
(iv) 42 वर्ष।
प्रश्न 12.
स्वामी महावीर जी को ज्ञान की प्राप्ति कहाँ हुई थी ?
(i) जरिमबिक गाँव
(ii) बौद्ध गया
(ii) वैशाली
(iv) कुंडग्राम।
उत्तर-
(i) जरिमबिक गाँव
प्रश्न 13.
निम्नलिखित में कौन-सा स्वामी महावीर जी का प्रचार केंद्र नहीं था ?
(i) राजगृह
(ii) वैशाली
(iii) अंग
(iv) पुरुषपुर।
उत्तर-
(iv) पुरुषपुर।
प्रश्न 14.
स्वामी महावीर जी को कहाँ निर्वाण प्राप्त हुआ था ?
(i) विदेह
(ii) अंग
(iii) राजगृह
(iv) पावा।
उत्तर-
(iv) पावा।
प्रश्न 15.
स्वामी महावीर जी की निर्वाण प्राप्ति के समय उनकी आयु कितनी थी ?
(i) 60 वर्ष
(ii) 62 वर्ष
(iii) 72 वर्ष
(iv) 80 वर्ष।
उत्तर-
(iii) 72 वर्ष
प्रश्न 16.
निम्नलिखित में से कौन-सा धर्म त्रि-रत्नों में विश्वास रखता था ?
(i) बौद्ध धर्म
(ii) जैन धर्म
(iii) ईसाई धर्म
(iv) पारसी धर्म।
उत्तर-
(ii) जैन धर्म
प्रश्न 17.
जैन धर्म कितनी सच्चाइयों में विश्वास रखता है ?
(i) 3
(i) 5
(iii) 7
(iv) 9.
उत्तर-
(iv) 9.

प्रश्न 18.
जैन धर्म जीव के बंधन का मुख्य कारण किसे मानते हैं ?
(i) पाप
(ii) पुण्य
(iii) मोक्ष
(iv) अजीव।
उत्तर-
(i) पाप
प्रश्न 19.
निम्नलिखित में से कौन-सी स्वामी महावीर जी की शिक्षा नहीं है ?
(i) वह अहिंसा में विश्वास रखते थे
(ii) वह कर्म सिद्धांत में विश्वास रखते थे ।
(iii) वह समानता में विश्वास रखते थे
(iv) वह ईश्वर में विश्वास रखते थे।
उत्तर-
(iv) वह ईश्वर में विश्वास रखते थे।
प्रश्न 20.
जैन धर्म कितने अनुव्रतों में विश्वास रखता है ?
(i) 3
(ii) 5
(iii) 7
(iv) 9.
उत्तर-
(ii) 5
प्रश्न 21.
जैन धर्म के अनुसार हिंसा कितने प्रकार की होती है ?
(i) 2
(ii) 3
(iii) 4
(iv) 5.
उत्तर-
(i) 2
प्रश्न 22.
कौन-सा तत्व जीव और पुदगल के मध्य गति पैदा करता है ?
(i) पुदगल
(ii) धर्म
(iii) अधर्म
(iv) पाप।
उत्तर-
(ii) धर्म
प्रश्न 23.
अजीविक संप्रदाय का संस्थापक कौन था ?
(i) गोशाल
(ii) स्वामी महावीर
(iii) वीराजी
(iv) भीखनजी।
उत्तर-
(i) गोशाल
प्रश्न 24.
निम्नलिखित में से कौन जैन धर्म के साथ संबंधित संप्रदाय नहीं हैं ?
(i) दिगंबर
(ii) श्वेतांबर
(iii) लोंक
(iv) महायान।
उत्तर-
(iv) महायान।

प्रश्न 25.
निम्नलिखित में से कौन-सा धर्म जैन धर्म के साथ संबंधित नहीं है ?
(i) दीपवंश
(ii) कल्पसूत्र
(iii) भगवती सूत्र
(iv) आचारंग सूत्र।
उत्तर-
(i) दीपवंश
![]()
![]()
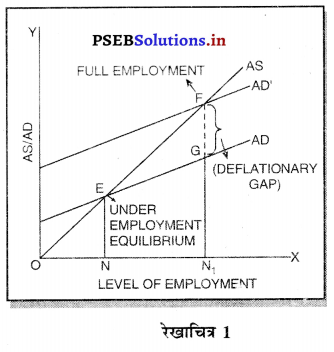
![]()
![]()
![]()