PSEB 12th Class Maths Solutions Chapter 5 Continuity and Differentiability Ex 5.6

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 5 Continuity and Differentiability Ex 5.6 Textook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.6

Direction (1 – 10) : If x and y are connected parametrically by the equations, given in the following questions without eliminating the parameter, find

Question 1.
x = 2at², y = at⁴
Solution.
The given equations are x = 2at² and y = at⁴
On differentiating w.r.t. t, we get
\(\frac{d x}{d t}\) = \(\frac{d}{d t}\) (2at²)
= 2a . \(\frac{d}{d t}\) (t²)
= 2a . 2t = 4at

and \(\frac{d y}{d t}\) = \(\frac{d}{d t}\) (at⁴)
= a . \(\frac{d}{d t}\) (t⁴)
= a . 4 . t³
= 4at³

∴ \(\frac{d y}{d x}=\frac{\left(\frac{d y}{d t}\right)}{\left(\frac{d x}{d t}\right)}=\frac{4 a t^{3}}{4 a t}\) = t²

(∴ \(\frac{d y}{d x}=\frac{d y / d t}{d x / d t}\))

Question 2.
x = a cos θ, y = b cos θ
Solution.
The given equations are x = a cos θ and y = b cos θ
On differentiating w.r.t. θ, we get
\(\frac{d x}{d θ}\) = \(\frac{d}{d θ}\) (a cos θ)
= a (- sin θ) = – a sin θ
and \(\frac{d y}{d θ}\) = \(\frac{d}{d θ}\) (cos θ)
= b (- sin θ) = – sin θ
∴ \(\frac{d y}{d x}=\frac{\left(\frac{d y}{d \theta}\right)}{\left(\frac{d x}{d \theta}\right)}=\frac{-b \sin \theta}{-a \sin \theta}=\frac{b}{a}\)

Question 3.
x = sin t, y = cos 2t
Solution.
The given equations are x = sin t and y = cos 2t
On differentiating w.r.t. t, we get
\(\frac{d x}{d t}\) = \(\frac{d}{d t}\) (sin t) = cos t
and \(\frac{d y}{d t}\) = \(\frac{d}{d t}\) (cos 2t)
= – sin (2t) . \(\frac{d}{d t}\) (2t) = – 2 sin 2t
∴ \(\frac{d y}{d x}=\frac{\left(\frac{d y}{d t}\right)}{\left(\frac{d x}{d t}\right)}\)

= \(\frac{-2 \sin 2 t}{\cos t}=\frac{-2 \cdot 2 \sin t \cos t}{\cos t}\)
= – 4 sin t.

Question 4.
x = 4t, y = \(\frac{4}{t}\)
Sol.
The given equations are x = 4t and y = \(\frac{4}{t}\)
On differentiating w.r.t. t, we get

Question 5.
x = cos θ – cos 2θ, y = sin θ – sin 2θ
Solution.
The given equations are x = cos θ – cos 2θ, y = sin θ – sin 2θ
On differentiating w.r.t θ, we get
\(\frac{d x}{d θ}\) = \(\frac{d}{d θ}\) (cos θ – cos 2θ)

= \(\frac{d}{d θ}\) (cos θ) – \(\frac{d}{d θ}\) (cos 2θ)
= – sin θ – (- sin 2θ)
= 2 sin 2θ – sin θ

and \(\frac{d y}{d θ}\) = \(\frac{d}{d θ}\) (sin θ – sin 2θ)

= \(\frac{d}{d θ}\) (sin θ) – \(\frac{d}{d θ}\) (sin 2θ)
= cos θ – 2 cos 2θ
∴ \(\frac{d y}{d x}=\frac{\left(\frac{d y}{d \theta}\right)}{\left(\frac{d x}{d \theta}\right)}=\frac{\cos \theta-2 \cos 2 \theta}{2 \sin 2 \theta-\sin \theta}\)

Question 6.
x = a (θ – sin θ), and y = a(1 + cos θ)
Solution.
The given equations are x = a (θ – sin θ), and y = a(1 + cos θ)
On differentiating w.r.t x, we get
\(\frac{d x}{d θ}\) = a [\(\frac{d}{d θ}\) (θ) – \(\frac{d}{d θ}\) (sin θ)]
= a (1 – cos θ)

and \(\frac{d y}{d θ}\) = a[\(\frac{d}{d θ}\) (1) + \(\frac{d}{d θ}\) (cos \(\frac{d}{d θ}\))]
= a[0 + (- sin θ)]
– a sin θ
∴ \(\frac{d y}{d x}=\frac{\left(\frac{d y}{d \theta}\right)}{\left(\frac{d x}{d \theta}\right)}=\frac{-a \sin \theta}{a(1-\cos \theta)}\)

= \(\frac{-2 \sin \frac{\theta}{2} \cos \frac{\theta}{2}}{2 \sin ^{2} \frac{\theta}{2}}=\frac{-\cos \frac{\theta}{2}}{\sin \frac{\theta}{2}}=-\cot \frac{\theta}{2}\)

Question 7.
x = \(\frac{\sin ^{3} t}{\sqrt{\cos ^{2} t}}\), y = \(\frac{\cos ^{3} t}{\sqrt{\cos 2 t}}\)
Solution.
The given equations are x = \(\frac{\sin ^{3} t}{\sqrt{\cos ^{2} t}}\), y = \(\frac{\cos ^{3} t}{\sqrt{\cos 2 t}}\)
On differentiating w.r.t t, we get

Question 8.
x = a(cos t + log tan \(\frac{t}{2}\)), y = a sin t
Solution.
The given equations are x = a (cos t + log tan \(\frac{t}{2}\)) and y = a sin t
On differentiating w.r.t t, we get

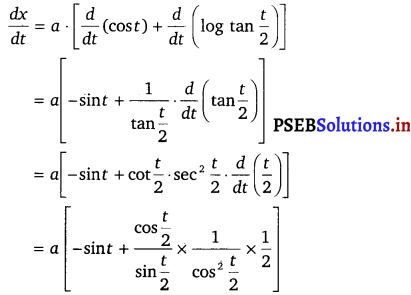
Question 9.
x = a sec θ, y = b tan θ
Solution.
The given equations are x = a sec θ and y = b tan θ
On differentiating w.r.t to θ, we get
\(\frac{d x}{d θ}\) = a . \(\frac{d}{d θ}\) (sec θ)
= a sec θ tan θ

and \(\frac{d y}{d θ}\) = b . \(\frac{d}{d θ}\) (tan θ)
= b sec² θ

∴ \(\frac{d y}{d x}=\frac{\left(\frac{d y}{d \theta}\right)}{\left(\frac{d x}{d \theta}\right)}=\frac{b \sec ^{2} \theta}{a \sec \theta \tan \theta}\)

= \(\frac{b}{a}\) sec θ cot θ

= \(\frac{b \cos \theta}{a \cos \theta \sin \theta}=\frac{b}{a} \times \frac{1}{\sin \theta}=\frac{b}{a} \ {cosec} \theta\)

Question 10.
x = a (cos θ + θ sin θ), y = a (sin θ – θ cos θ)
Solution.
The given equations are x = a (cos θ + θ sin θ), y = a (sin θ – θ cos θ)
On differentiating w.r.t to θ, we get

\(\frac{d x}{d θ}\) = a [\(\frac{d}{d θ}\) (cos θ ) + \(\frac{d x}{d θ}\) (θ sin θ)]

= a [- sin θ + θ \(\frac{d}{d θ}\) (sin θ) + sin θ \(\frac{d}{d θ}\) (θ)]

= a [- sin θ + θ cos θ + sin θ] = a θ cos θ

and \(\frac{d y}{d θ}\) = a [\(\frac{d}{d θ}\) (sin θ) – \(\frac{d}{d θ}\) (θ cos θ)]

= a [cos θ – {θ latex]\frac{d}{d θ}[/latex] (cos θ) + cos θ . latex]\frac{d}{d θ}[/latex] (θ)}]

= a [cos θ + θ sin θ – cos θ] = aθ sin θ

∴ \(\frac{d y}{d x}=\frac{\left(\frac{d y}{d \theta}\right)}{\left(\frac{d x}{d \theta}\right)}=\frac{a \theta \sin \theta}{a \theta \cos \theta}\) = tan θ.

Question 11.
If x = \(\sqrt{a^{\sin ^{-2} t}}\), y = \(\sqrt{a^{\cos ^{-1} t}}\), show that \(\frac{d y}{d x}=-\frac{y}{x}\).
Solution.
The given equations are x = \(\sqrt{a^{\sin ^{-2} t}}\) and y = \(\sqrt{a^{\cos ^{-1} t}}\)

⇒ x = \(\sqrt{a^{\sin ^{-2} t}}\) and y = \(\sqrt{a^{\cos ^{-1} t}}\)

Consider x = \(a^{\frac{1}{2} \sin ^{-1} t}\)
Taking logarithm on bothsides, we get
log x = \(\frac{1}{2}\) sin^-1 t log a

⇒ \(\frac{1}{x} \cdot \frac{d x}{d t}=\frac{1}{2} \log a \cdot \frac{d}{d t}\left(\sin ^{-1} t\right)\)

⇒ \(\frac{d x}{d t}=\frac{x}{2} \log a \cdot \frac{1}{\sqrt{1-t^{2}}}\)

⇒ \(\frac{d x}{d t}=\frac{x \log a}{2 \sqrt{1-t^{2}}}\)

Then, consider y = \(a^{\frac{1}{2} \cos ^{-1} t}\)

Taking logarithm on bothsides, we get

Hence proved.