PSEB 12th Class Maths Solutions Chapter 5 Continuity and Differentiability Miscellaneous Exercise

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 5 Continuity and Differentiability Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Miscellaneous Exercise

Direction (1 – 11) :
Differentiate the following functions with respect to x.
Question 1.
(3x² – 9x + 5)⁹
Solution.
Let y = (3x² – 9x + 5)⁹
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (3x² – 9x + 5)⁹
= 9(3x² – 9x + 5)⁸ – (3x² – 9x + 5) dx
= 9(3x² – 9x + 5)⁸ . ⁸ (6x – 9)
= 9(3x² – 9x + 5)⁸ . 3(2x – 3)
= 27(3x² – 9x + 5)⁸ (2x – 3)

Question 2.
sin³ x + cos⁶ x
Solution.
Let y = sin³ x + cos⁶ x
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (sin³ x) + \(\frac{d}{d x}\) (cos⁶ x)
= 3 sin² x \(\frac{d}{d x}\) (sin x) + 6 cos⁵ x . \(\frac{d}{d x}\) (cos x)
= 3 sin² x cos x + 6 cos⁵ x . (- sin x)
= 3 sin x cos x (sin x – 2 cos⁴ x).

Question 3.
(5x)^{3 cos 2x}
Solution.
Let y = (5x)^{3 cos 2x}
Taking logarithm on both sides, we get
log y = 3 cos 2x log 5x
Differentiating on both sides w.r.t. x, we get
\(\frac{1}{y}\) \(\frac{d y}{d x}\) = 3 [log 5x . \(\frac{d}{d x}\) (cos 2x) + cos 2x . \(\frac{d}{d x}\) (log 5x)]

⇒ \(\frac{d y}{d x}\) = 3y [log 5x (- sin 2x) . \(\frac{d}{d x}\) (2x) + cos 2x . \(\frac{1}{5 x}\) . \(\frac{d}{d x}\) (5x)]

⇒ \(\frac{d y}{d x}\) = 3y [- 2 sin 2x log 5x + \(\frac{\cos 2 x}{x}\)]

⇒ \(\frac{d y}{d x}\) = y [\(\frac{3 \cos 2 x}{x}\) – 6 sin 2x log 5x]

∴ \(\frac{d y}{d x}\) = (5x)^{3 cos 2x} [\(\frac{3 \cos 2 x}{x}\) – 6 sin 2x log 5x]

Question 4.
sin^-1(x√x), 0 ≤ x ≤ 1
Solution.
Let y = sin^-1 (x√x)
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) sin^-1 (x√x)
= \(\frac{1}{\sqrt{1-(x \sqrt{x})^{2}}} \times \frac{d}{d x}(x \sqrt{x})\)

= \(\frac{1}{\sqrt{1-x^{3}}} \cdot \frac{d}{d x}\left(x^{\frac{3}{2}}\right)\)

= \(\frac{1}{\sqrt{1-x^{3}}} \times \frac{3}{2} \cdot x^{\frac{1}{2}}\)

= \(\frac{3 \sqrt{x}}{2 \sqrt{1-x^{3}}} \Rightarrow \frac{3}{2} \sqrt{\frac{x}{1-x^{3}}}\)

Question 5.
\(\frac{\cos ^{-1} \frac{x}{2}}{\sqrt{2 x+7}}\), – 2 < x < 2
Solution.
Let y = \(\frac{\cos ^{-1} \frac{x}{2}}{\sqrt{2 x+7}}\)
Differentiating w.r.t. x, we get

Question 6.
cot^-1 \(\left[\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right]\), 0 < x < \(\frac{\pi}{2}\)
Solution.

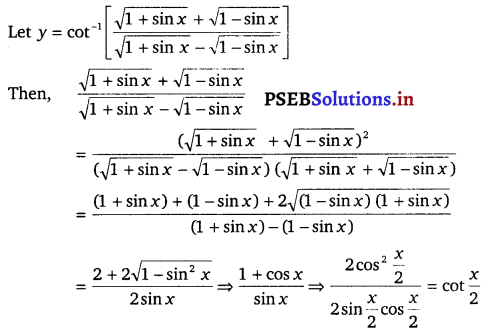
Therefore, Eq. (i) becomes
y = cot^-1 (cot \(\frac{x}{2}\))
⇒ y = \(\frac{x}{2}\)
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{1}{2}\) \(\frac{d}{d x}\) (x)
⇒ \(\frac{d y}{d x}\) = \(\frac{1}{2}\).

Question 7.
(log x)^{log x}, x > 1
Solution.
Let y = (log x)^{log x}
Taking logarithm on both sides, we get
log y = log (log x)log x
⇒ log y = log x . log(log x)
Differentiating both sides w.r.t. x, we get
\(\frac{1}{y}\) . \(\frac{d y}{d x}\) = \(\frac{d}{d x}\) [log x . log(log x)] y
⇒ \(\frac{1}{y}\) . \(\frac{d y}{d x}\) = log (log x) . \(\frac{d}{d x}\) (log x) + log x . \(\frac{d}{d x}\) [log (log x)]

⇒ \(\frac{d y}{d x}\) = y [log (log x) . \(\frac{1}{x}\) + log x . \(\frac{1}{\log x}\) . \(\frac{d}{d x}\) (log x)]

⇒ \(\frac{d y}{d x}\) = y [\(\frac{1}{x}\) log (log x) + \(\frac{1}{x}\)]

∴ \(\frac{d y}{d x}\) = (log x)^{log x} [\(\frac{1}{x}\) log (log x) + \(\frac{1}{x}\)]

Question 8.
cos(a cos x + b sin x), for some constant a and b.
Solution.
Let y = cos(acosx + bsinx)
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) cos(a cos x + b sin x)
\(\frac{d y}{d x}\) = – sin(a cos x + b sin x) . \(\frac{d}{d x}\) (a cos x + b sin x)
= – sin(a cos x + b sin x) . [a (- sin x) + b cos x]
= (a sin x – b cos x) . sin (a cos x + b sin x).

Question 9.
(sin x – cos x)^{(sin x – cos x)}, \(\frac{\pi}{4}<x<\frac{3 \pi}{4}\)
Solution.
Let y = (sin x – cos x) (sin x – cos x)
Taking logarithm on both sides, we get
log y = log (sin x – cos x)[(sin x – cos x)^{(sin x – cos x)}]
⇒ log y = (sin x – cos x) . log(sin x – cos x)
Differentiating on both sides w.r.t. x, we get
\(\frac{1}{y}\) . \(\frac{d y}{d x}\) = \(\frac{d}{d x}\) [(sin x – cos x) log(sin x – cos x)]

⇒ \(\frac{1}{y}\) . \(\frac{d y}{d x}\) = log (sin x – cos x) . \(\frac{d}{d x}\) log (sin x – cos x) – (sin x – cos x) + (sin x – cos x) . \(\frac{d}{d x}\) log (sin x – cos x)

⇒ \(\frac{d y}{d x}\) = (sin x – cos x)^{(sin x – cos x)} [(cos x + sin x) . log (sin x – cos x) + (cos x – sin x)]

∴ \(\frac{d y}{d x}\) = (sin x – cos x)^{(sin x – cos x)} (cos x + sin x) [1 + log (sin x – cos x)]

Question 10.
x^x + x^a + a^x + a^a, for some fixed a > 0 and x > 0.
Solution.
Let y = x^x + x^a + a^x + a^a
Also, let x^x = u, x^a = v, a^x = w, and a^a = s
∴ y = u + v + w + s
Differentiating w.r.t. x, we get

\(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}+\frac{d w}{d x}+\frac{d s}{d x}\) ……………(i)

Then, u = x^x
⇒ log u = log x^x (Taking log on both sides)
⇒ log u = x logx
Differentiating on both sides w.r.t. x, we get
\(\frac{1}{u}\) \(\frac{d u}{d x}\) = log x . \(\frac{d}{d x}\) (x) + x . \(\frac{d}{d x}\) (log x)
⇒ \(\frac{d u}{d x}\) = u [log x . 1 + x . \(\frac{1}{x}\)]

⇒ \(\frac{d u}{d x}\) = x^x [log x + 1]
= x^x (1 + log x) …………..(ii)

v = x^a
Differentiating w.r.t. x, we get
\(\frac{d v}{d x}\) = \(\frac{d}{d x}\) (x^a)

⇒ \(\frac{d v}{d x}\) = a x^{a – 1} ………….(iii)

w = a^x
⇒ log w = log a^x
⇒ log w = a log x
Differentiating on both sides w.r.t. x, we get
⇒ \(\frac{d w}{d x}\) = log a . \(\frac{d}{d x}\) (x)

⇒ \(\frac{d w}{d x}\) = a^x log a ………………(iv)

s = a^a
Since, a is constant, therefore a^a is also a constant.
∴ \(\frac{d s}{d x}\) = 0 …………..(v)
From Eqs. (i), (ii), (iii), (iv) and (v), we get
\(\frac{d y}{d x}\) = x^x (1 + log x) + a x^{a – 1} + a^x log a + 0
= xx^x (1 + log x) + a x^{a – 1} + a^x log a.

Question 11.
x^{x2 – 3} + (x – 3)^x2, for x > 3.
Solution.
Let y = x^{x2 – 3} + (x – 3)^x2
Also, let u = x^{x2 – 3} and v = (x – 3)^x2
∴ y = u + v
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\)
Then, u = x^{x2 – 3}
Taking log on both sides, we get
log u = log x^{x2 – 3}
= (x² – 3) log x
Differentiating w.r.t. x, we get
\(\frac{1}{u}\) \(\frac{d u}{d x}\) = 2x log x + (x² – 3) log x × \(\frac{1}{x}\)

∴ \(\frac{d u}{d x}\) = u (2x log x + \(\frac{x^{2}-3}{x}\))
= x^{x2 – 3} (2x log x + \(\frac{x^{2}-3}{x}\)) …………….(ii)
Also, v = (x – 3)^{x2
Differentiating on both sides, we get
\(\frac{1}{v}\) \(\frac{d v}{d x}\) = \(\frac{d v}{d x}\) [2x log (x – 3) + \(\frac{x^{2}-3}{x}\)] ……………..(iii)
From Eqs. (i), (ii) and (iii), we get
\(\frac{d y}{d x}\) = xx2 – 3 \(\left(2 x \log x+\frac{x^{2}-3}{x}\right)+(x-3)^{x^{2}}\left[2 x \log (x-3)+\frac{x^{2}}{x-3}\right]\)}

Question 12.
Find \(\frac{d y}{d x}\), if y = 12 (1 – cos t), x = 10 (t – sin t), \(-\frac{\pi}{2}<t<\frac{\pi}{2}\)
Solution.
Given, y = 12 (1 – cos t) and x = 10 (t – sin t)
Differentiating w.r.t t, we get
\(\frac{d x}{d t}\) = \(\frac{d}{d t}\) [10 (t – sin t)]
= 10 . \(\frac{d}{d t}\) (t – sin t)
= 10 (1 – cos t)

and \(\frac{d y}{d t}\) = \(\frac{d}{d t}\) [12 (1 – cos t)]
= 12 . \(\frac{d}{d t}\) (1 – cos t)
= 12 . [0 – (- sin t)] = 12 sin t

Now, \(\frac{d y}{d x}\) = \(\frac{\left(\frac{d y}{d t}\right)}{\left(\frac{d x}{d t}\right)}=\frac{12 \sin t}{10(1-\cos t)}\)

= \(\frac{12 \cdot 2 \sin \frac{t}{2} \cdot \cos \frac{t}{2}}{10 \cdot 2 \sin ^{2} \frac{t}{2}}=\frac{6}{5} \cot \frac{t}{2}\).

Question 13.
Find \(\frac{d y}{d x}\), if y = sin^-1 x + sin^-1 \(\sqrt{1-x^{2}}\), – 1 ≤ x ≤ 1.
Solution.
Given, y = sin^-1 x + sin^-1 \(\sqrt{1-x^{2}}\)
putting x = sin θ in above eq., we get
y = sin^-1 sin θ + sin^-1 \(\sqrt{1-(\sin \theta)^{2}}\)
y = θ + sin^-1 \(\sqrt{1-(\sin \theta)^{2}}\)
= θ + sin^-1 (cos θ)
= θ + sin^-1 sin (\(\frac{\pi}{2}\) – θ)
= θ + \(\frac{\pi}{2}\) – θ
Differentiating w.r.t x, we get
∴ \(\frac{d y}{d x}\) = 0

Question 14.
If x \(\sqrt{1+y}\) + y \(\sqrt{1+x}\) = 0, for – 1 < x < 1, prove that \(\frac{d y}{d x}=\frac{1}{(1+x)^{2}}\).
Solution.
Given, x \(\sqrt{1+y}\) + y \(\sqrt{1+x}\) = 0
⇒ x \(\sqrt{1+y}\) = – y \(\sqrt{1+x}\)
On squaring bothsides, we get
x² (1 + y) = y² (1 + x)
⇒ x² + x²y = y² + xy²
⇒ x² – y² = xy² – x²y
⇒ x² – y² = xy (y – x)
⇒ (x + y) (x – y) = xy (y – x)
∴ x + y = -xy
⇒ (1 + x) y = – x
⇒ y = \(\frac{-x}{(1+x)}\)
Differentiating on bothsides w.r.t x, we get
\(\frac{d y}{d x}\) = \(\frac{(1+x) \frac{d}{d x}(x)-x \frac{d}{d x}(1+x)}{(1+x)^{2}}\)

= \(-\frac{(1+x)-x}{(1+x)^{2}}=-\frac{1}{(1+x)^{2}}\)

Hence proved.

Question 15.
If (x – a)² + (y – b)² = c², for some c > 0, prove that \(\frac{\left(1+\left(\begin{array}{l}
d y \\
d x
\end{array}\right)^{2}\right]^{3}}{d^{2} y} \frac{d x^{2}}{}\) is a constant independent of a and b.
Solution.
Given, (x – a)² + (y – b)² = c²
Differentiating on both sides w.r.t. x. we get
\(\frac{d}{d x}\) [(x – a)²] + \(\frac{d}{d x}\) [(y – b)²] = \(\frac{d}{d x}\) (c²)
⇒ 2 (x – a) . \(\frac{d}{d x}\) (x – a) + 2 (y – b) . \(\frac{d}{d x}\) (y – b) = 0
⇒ 2 (x – a) . 1 + 2(y – b) . \(\frac{d y}{d x}\) = 0
⇒ \(\frac{d y}{d x}\) = \(\frac{-(x-a)}{y-b}\) ………………(i)
Again, differentiating w.r.t. x, we get
∴ \(\frac{d^{2} y}{d x^{2}}\) = \(\frac{d}{d x}\left[\frac{-(x-a)}{y-b}\right]\)

= – \(\left[\frac{(y-b) \cdot \frac{d}{d x}(x-a)-(x-a) \cdot \frac{d}{d x}(y-b)}{(y-b)^{2}}\right]\)

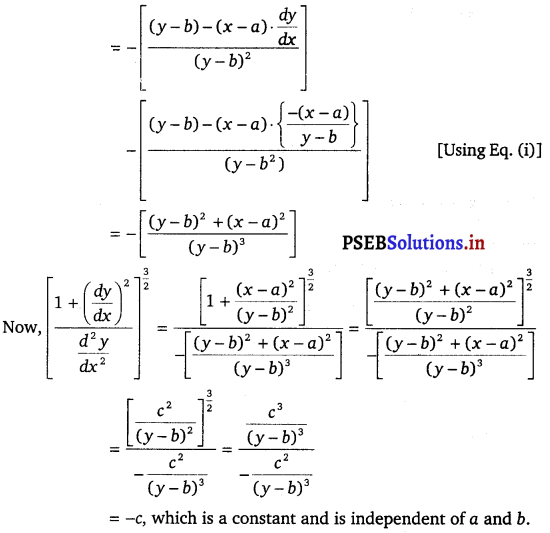
Hence proved.

Question 16.
If cos y = x cos (a + y), with cos a ≠ ± 1, prove that \(\frac{d y}{d x}=\frac{\cos ^{2}(a+y)}{\sin a}\).
Solution.
Given, cos y = x cos(a + y)
Differentiating w.r.t. x, we get
\(\frac{d}{d x}\) [cos y] = \(\frac{d}{d x}\) [x cos (a + y)]
⇒ – sin y = cos (a + y) . \(\frac{d}{d x}\) (x) + x . \(\frac{d}{d x}\) [cos (a + y)]
⇒ – sin y \(\frac{d y}{d x}\) = cos (a + y) + x [- sin (a + y)]
⇒ [x sin (a + y) – sin y] \(\frac{d y}{d x}\) = cos (a + y) ……………(i)
∵ cos y = x cos (a + y), x = \(\frac{\cos y}{\cos (a+y)}\)
Then, Eq. (i) reduces to
[\(\frac{\cos y}{\cos (a+y)}\) . sin (a + y) – sin y] \(\frac{d y}{d x}\) = cos (a + y)
⇒ [cos y . sin (a + y)] – sin y . cos (a + y)] . \(\frac{d y}{d x}\) = cos ² (a + y)
⇒ sin (a + y – y) \(\frac{d y}{d x}\) = cos² (a + y)
⇒ \(\frac{d y}{d x}\) = \(\frac{\cos ^{2}(a+y)}{\sin a}\).
Hence proved.

Question 17.
If x = a(cos t + t sin t) and y = a(sin t – t cos t), find \(\frac{d^{2} y}{d x^{2}}\).
Solution.
Given, x = a (cos t + t sin t) and y = a (sin t – t cos t)
Differentiating both Eqs. w.r.t. t, we get
∴ \(\frac{d x}{d t}\) = a \(\frac{d}{d t}\) (cos t + t sin t)

= a [- sin t + sin t . \(\frac{d}{d x}\) (t) + t . \(\frac{d}{d t}\) (sin t)]

= a [- sin t + sin t + t cos t] = at cost
Also, \(\frac{d y}{d t}\) = a \(\frac{d}{d t}\) (sin t – t cost)

= a [cos t – {cos t . \(\frac{d}{d t}\) (t) + t . \(\frac{d}{d t}\) (cost)}]
= a [cos t – {cos t – t sin t}] = at sin t

\(\frac{d y}{d x}\) = \(\frac{\left(\frac{d y}{d t}\right)}{\left(\frac{d x}{d t}\right)}=\frac{a t \sin t}{a t \cos t}\) = tan t
Again, differentiating w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac{d}{d x}\) (tan t)

= sec² t . \(\frac{d t}{d x}\)

[∵ \(\frac{d x}{d t}\) = at cos t
⇒ \(\frac{d t}{d x}\) = \(\frac{1}{a t \cos t}\)]

= sec² t . \(\frac{1}{a t \cos t}\)

= \(\frac{\sec ^{3} t}{a t}\), 0 < t < \(\frac{\pi}{2}\)

Question 18.
If f(x) = |x|³, show that f”(x) exists for all real x and find it.
Solution.
Here, f(x) = | x |³
When x > 0, f(x) = |x|³ = x³
Differentiating both sides w.r.t. x, we get
\(\frac{d}{d x}\) [f(x)] = \(\frac{d}{d x}\) (x³)
⇒ f'(x) = 3x²
Again, differentiating both sides w.r.t. x, we get
\(\frac{d}{d x}\) [f'(x)] = \(\frac{d}{d x}\) (3x²)
⇒ f”(x) = 6x
When x < 0,
f(x) = |x|³ = – x³
Differentiating both sides w.r.t. x, we get
\(\frac{d}{d x}\) [f(x)] = \(\frac{d}{d x}\) (- x³)
⇒ f'(x) = – 3x²
Again, differentiating both sides w.r.t. x, we get
\(\frac{d}{d x}\) [f'(x)] = \(\frac{d}{d x}\) (- 3x²) = – 6x
f”(x) = – 6x
Hence,f”(x) =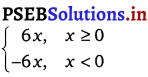

Question 19.
Using mathematical induction, prove that \(\frac{d}{d x}\) (xⁿ) = n x^{n – 1} for all positive integers n.
Solution.
Let P(n): \(\frac{d}{d x}\) (xⁿ) = nx^{n – 1} for all positive integers n
For n = 1,
P(1): \(\frac{d}{d x}\)(x) = 1 = 1 . x^{1 – 1}
∴ P(n) is true for n = 1.
Let P(k) is true for some positive integer k.
i.e., P(k): \(\frac{d}{d x}\) (x^k) = k x^{k – 1}
It has to be proved that P(k +1) is also true.
Consider \(\frac{d}{d x}\) (x^{k – 1}1) = \(\frac{d}{d x}\) (x . x^k)
= x^k . \(\frac{d}{d x}\) (x) + x . \(\frac{d}{d x}\) (x^k) [Applying product rule]
= (k + 1) . x^k
= (k + 1) . x^{(k+1) – 1}
Thus, P(k + 1) is true whenever P(k) is true.
Therefore, by the principle of mathematical induction, the statement P(n) is true for every positive integer n. Hence proved.

Question 20.
Using the fact that sin (A + B) = sin A cos B + cos A sin B and the differentiation, obtain the sum formula for cosines.
Solution.
We have, sin(A + B) = sin A cos B + cos A sin B
Differentiating on both sides w.r.t. x, we get
⇒ \(\frac{d}{d x}\) [sin(A + B)] = \(\frac{d}{d x}\) (sin A cos B) + \(\frac{d}{d x}\) (cos A sin B)

⇒ cos (A + B) . \(\frac{d}{d x}\) (A + B) = cos B . \(\frac{d}{d x}\) (sin A) + sin A . \(\frac{d}{d x}\) (cos B) + sin B . \(\frac{d}{d x}\) (cos A) + cos A . \(\frac{d}{d x}\) (sin B)
⇒ cos (A + B) . \(\frac{d}{d x}\) (A + B) = cos B cos A \(\frac{d A}{d x}\) + sin A(- sin B) \(\frac{d B}{d x}\) + sin B (- sin A) . \(\frac{d A}{d x}\) + cos A cos B \(\frac{d B}{d x}\)
cos (A + B) = cos A cos B – sin A sin B.

Question 21.
Does there exist a function which is continuous everywhere but not differentiable at exactly two points? Justify your answer.
Solution.
Yes, we have the continuous function f(x) = |x – 1| + |x – 2|, which is continuous at all x ∈ R but differentiable at all x except 1, 2.
Here, f(x) = |x – 1| + |x – 2|
=

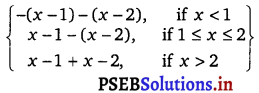
i.e., f(x) =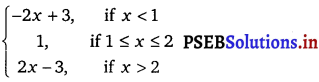
Since, polynomial function is continuous, so it is clear that f is continuous at all except possible at 1, 2.
Now, we have to check the continuity at 1, 2
At x = 1 f(1) = 1,
LHL = \(\lim _{x \rightarrow 1^{-}}\) f(x) = \(\lim _{x \rightarrow 1^{-}}\) (- 2x + 3)
= – 2 + 3 = 1

RHL = \(\lim _{x \rightarrow 1^{+}}\) f(x) = \(\lim _{x \rightarrow 1^{+}}\) 1 = 1

⇒ f(1) = \(\lim _{x \rightarrow 1^{-}}\) f(x) = \(\lim _{x \rightarrow 1^{+}}\) f(x)
⇒ f is continuous at x = 1

At x = 2 f(2) = 1
⇒ LHL = \(\lim _{x \rightarrow 2^{-}}\) f(x) = \(\lim _{x \rightarrow 2^{-}}\) (1) = 1

RHL = \(\lim _{x \rightarrow 2^{+}}\) f(x) = \(\lim _{x \rightarrow 2^{+}}\) (2x – 3)
= 2 × 2 – 3 = 1

f(x) = \(\lim _{x \rightarrow 2^{-}}\) f(x) = \(\lim _{x \rightarrow 2^{+}}\) f(x)

So, f is continuous at x = 2. Thus, f is continuous at all x ∈ R. -2, if x < 1

Lf'(2) ≠ Rf'(2)
⇒ f is not differentiale at 2.
Thus, we see that f(x) = |x – 1| + |x – 2| is continuous everywhere and differentiable also at all x ∈ R except at 1, 2.

Question 22.
If y = \(\begin{array}{ccc}
\boldsymbol{f}(\boldsymbol{x}) & \boldsymbol{g}(\boldsymbol{x}) & \boldsymbol{h}(\boldsymbol{x}) \\
\boldsymbol{l} & \boldsymbol{m} & \boldsymbol{n} \\
\boldsymbol{a} & \boldsymbol{b} & \boldsymbol{c}
\end{array}\), prove that \(\frac{d y}{d x}=\left|\begin{array}{ccc}
f^{\prime}(x) & g^{\prime}(x) & h^{\prime}(x) \\
l & m & n \\
a & b & c
\end{array}\right|\).
Solution.

Question 23.
If y = e^{a cos-1 x} ,- 1 ≤ x ≤ 1, show that (1 – x²) \(\frac{d^{2} y}{d x^{2}}\) – x \(\frac{d y}{d x}\) – a² y = 0.
Solution.
Given, y = e^{a cos-1 x}
Taking logarithm on bothsides, we get
⇒ log y = a cos^-1 x log e
⇒ log y = a cos^-1 x [∵ log e = 1]