Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 6 Application of Derivatives Ex 6.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 12 Maths Chapter 6 Application of Derivatives Ex 6.1
Question 1.
Find the rate of change of the area of a circle with respect to its radius r when
(a) r = 3 cm
(b) r = 4 cm
Solution.
The area of a circle (A) with radius (r) is given by
A = πr2
Now, the rate of change of the area with respect to its radius is given by
\(\frac{d A}{d r}\) = \(\frac{d}{d r}\) (πr2) = 2πr
(a) When, r = 3 cm
\(\frac{d A}{d r}\) = 2π(3) = 6π
Hence, the area of the circle is changing at the rate of 6π cm2/s when its radius is 3 cm.
(b) When r = 4 cm,
\(\frac{d A}{d r}\) = 2π(4) = 8π
Hence, the area of the circle is changing at the rate of 8π cm2/s when its radius is 4 cm.
![]()
Question 2.
The volume of a cube is increasing at the rate of 8 cm3/s. How fast is the surface area increasing when the length of an edge is 12 cm?
Solution.
Let x be the length of a side (edge), V be the volume and S be the surface area of the cube.
Then, V = x3 and S = 6x2 where, x is a function of time t.
It is given that \(\frac{d V}{d t}\) = 8 cm3 /s
Then, y using the chain rule, we have

Thus, when x = 12 cm,
\(\frac{d S}{d t}\) = \(\frac{32}{12}\) cm2/s
= \(\frac{8}{3}\) cm2/s
Hence, if the length of the edge of the cube is 12 cm, then the surface area is increasing at the rate of \(\frac{8}{3}\) cm2/s.
![]()
Question 3.
The radius of a circle is increasing uniformly at the rate of 3 cm/s. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
Solution.
The area of circle (A) with radius (r) is given by A = πr2
Now, the rate of change of area (A) with respect to time (t) is given by
It i s given that,
\(\frac{d r}{d t}\) = 3 cm/s
∴ \(\frac{d A}{d t}\) = 2πr (3) = 6πr
Thus, when r = 10 cm, dA
\(\frac{d A}{d t}\) = 6π(10) = 60π cm2/s dt
Hence, the rate at which the area of the circle is increasing when the radius is 10 cm, is 60π cm2/s.
Question 4.
An edge of a variable cube is increasing at the rate of 3 cm/s. How fast is the volume of the cube increasing when the edge is 10 cm long?
Solution.
Let x be the length of a side and V be the volume of the cube.
Then, V = x3
∴ \(\frac{d V}{d t}\) = 3x2 . \(\frac{d x}{d t}\)
It is given that,
\(\frac{d x}{d t}\) = 3 cm/sec
⇒ \(\frac{d V}{d t}\) = 3x2 (3) = 9x2
Thus, when x = 10 cm,
\(\frac{d V}{d t}\) = 9 (10)2 = 900 cm3/s
Hence, the volume of the cube is increasing at the rate of 900 cm3/s when the edge is 10 cm long.
![]()
Question 5.
A stone is dropped into a quiet lake and waves move in circles at the speed of 5 cm/s. At the instant when the radius of the circular wave is 8 cm, how fast is the enclosed area increasing?
Solution.
The area of a circle (A) with radius (r) is given by A = πr2.
Therefore, the rate of change of area (A) with respect to time (t) is given by
It is given that \(\frac{d r}{d t}\) = 5 cm/s dt
Thus, when r = 8 cm,
\(\frac{d A}{d t}\) = 2π (8) (5) = 80 π dt
Hence, when the radius of the circular wave is 8 cm, the enclosed area is increasing at the rate of 80π cm2/s.
Question 6.
The radius of a circle is increasing at the rate of 0.7 cm/s. What is the rate of increase of its circumference?
Solution.
The circumference of a circle (C) with radius (r) is given by C = 2nr
Therefore, the rate of change of circumference (C) with respect to time (t) is given by
\(\frac{d C}{d t}=\frac{d C}{d r} \cdot \frac{d r}{d t}\)
= \(\frac{d}{d r}(2 \pi r) \frac{d r}{d t}=2 \pi \cdot \frac{d r}{d r}\)
It is given that,
\(\frac{d r}{d t}\) = 0.7 cm/s
Hence, the rate of increase of the circumference is 2π (0.7) = 1.4π cm/s.
![]()
Question 7.
The length x of a rectangle is decreasing at the rate of 5 cm/min and the width y is increasing at the rate of 4 cm/min. When x = 8 cm and y = 6 cm, find the rates of change of
(a) the perimeter, and
(b) the area of the rectangle.
Solution.
Since, the length (x) is decreasing at the rate of 5 cm/min and the width (y) is increasing at the rate of 4 cm/min, we have
\(\frac{d x}{d t}\) = – 5 cm/min and
\(\frac{d y}{d t}\) = 4 cm/min
(a) The perimeter (P) of a rectangle is given by P = 2 (x + y)
∴ \(\frac{d P}{d t}=2\left(\frac{d x}{d t}+\frac{d y}{d t}\right)\)
= 2 (- 5 + 4) = – 2 cm/min
Hence, the perimeter is decreasing at the rate of 2 cm/min.
(b) The area (A) of a rectangle is given by A = x × y
∴ \(\frac{d A}{d t}=\frac{d x}{d t} \cdot y+x \cdot \frac{d y}{d t}\)
= – 5y + 4x
When x = 8 cm and y = 6 cm,
\(\frac{d A}{d t}\) = – 5 × 6 +4 × 8
= 2 cm2/min
Hence, the area of the rectangle is increasing at the rate of 2 cm2/min.
Question 8.
A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic cm of gas per second. Find the rate at which the radius of the balloon increases when the radius is 15 cm.
Solution.
The volume of a sphere (V) with radius (r) is given by
V = \(\frac{4}{3}\) πr3
∴ Rate of change of volume (V) with respect to time (r) is given by
\(\frac{d V}{d t}=\frac{d V}{d r} \cdot \frac{d r}{d t}\)
= \(\frac{d}{d r}\left(\frac{4}{3} \pi r^{3}\right) \cdot \frac{d r}{d t}=4 \pi r^{2} \cdot \frac{d r}{d t}\)
It is given that \(\frac{d V}{d t}{/latex] = 900 cm3/s
∴ 900 = 4πr2 . [latex]\frac{d r}{d t}\)
⇒ \(\frac{d r}{d t}\) = \(\frac{900}{4 \pi r^{2}}=\frac{225}{\pi r^{2}}\)
Therefore, when radius = 15 cm,
\(\frac{d r}{d t}=\frac{225}{\pi(15)^{2}}=\frac{1}{\pi}\).
![]()
Question 9.
A balloon, which always remains spherical, has a variable radius. Find the rate at which its volume is increasing with the radius when the later is 10 cm.
Solution.
The volume of a sphere (V) with radius (r) is gwen by V = \(\frac{4}{3}\) πr3.
Rate of change of volume (V) with respect to its radius (r) is given by
\(\frac{d V}{d r}=\frac{d}{d r}\left(\frac{4}{3} \pi r^{3}\right)\)
= \(\frac{4}{3}\) π (3r2) = 4πr2
Therefore, when radius = 10 cm,
\(\frac{d V}{d r}{/latex] = 4π(10)2 = 400π
Hence, the volume of the balloon is increasing at the rate of 400 π cm3/s.
Hence, the rate at which the radius of the balloon increases when the radius is 15 cm, is [latex]\frac{1}{\pi}\) cm/s.
Question 10.
A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall?
Solution.
Let y m be the height of the wall at which the ladder touches.
Also, let the foot of the ladder be x away from the wall.
Then, by Pythagoras theorem, we have
x2 + y2 = 25 [∵ Length of the ladder = 5 m]
⇒ y = \(\sqrt{25-x^{2}}\)
Then, the rate of change of height (y) with respect to time (t) is given by
It is given that \(\frac{d x}{d t}\) = 2 cm/s dt
∴ \(\frac{d y}{d t}=\frac{-2 x}{\sqrt{25-x^{2}}}\)
Now, when x = 4 m, we have
∴ \(\frac{d y}{d t}=\frac{-2 \times 4}{\sqrt{25-4^{2}}}=-\frac{8}{3}\)
Hence, the height of the ladder on the wall is decreasing at the rate of \(\frac{8}{3}\) cm/s.
![]()
Question 11.
A particle moves along the curve 6y = x3 + 2. Find the points on the curve at which the y – coordinate is changing 8 times as fast as the x – coordinate.
Solution.
The equation of the curve is given as 6y = x3 + 2
The rate of change of the position of the particle with respect to time (t) is given by
\(6 \frac{d y}{d t}=3 x^{2} \frac{d x}{d t}+0\)⇒ \(2 \frac{d y}{d t}=x^{2} \frac{d x}{d t}\)
When the y – coordinate of the particle changes 8 times as fast as the x-coordinate i.e., \(\left(\frac{d y}{d t}=8 \frac{d x}{d t}\right)\), we have
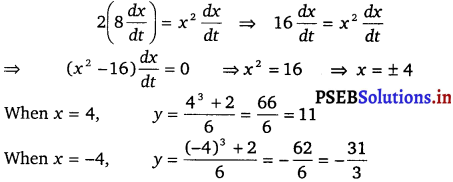
Hence, the points required on the curve are (4, 11) and (- 4, \(-\frac{31}{3}\)).
Question 12.
The radius of an air bubble is increasing at the rate of \(\frac{1}{2}\) cm/s; At what rate is the volume of the bubble increasing when the radius is 1 cm?
Solution.
The air bubble is in the shape of a sphere.
Now, the volume of an air bubble (V) with radius (r) is given by
V = \(\frac{4}{3}\) πr3.
The rate of change of volume (V) with respect to time (t) is given by
\(\frac{d V}{d t}=\frac{4}{3} \pi \frac{d}{d r}\left(r^{3}\right) \cdot \frac{d r}{d t}\)
= \(\frac{4}{3} \pi\left(3 r^{2}\right) \frac{d r}{d t}=4 \pi r^{2} \frac{d r}{d t}\)
It is given that \(\frac{d r}{d t}\) = \(\frac{1}{2}\) cm/s
Therefore, when r = 1 cm,
\(\frac{d V}{d t}\) = 4π(1)2 (\(\frac{1}{2}\))
= 2π cm3/s
Hence, the rate at which the volume of the bubble increases, is 2π cm3/s.
![]()
Question 13.
A balloon, which always remains spherical, has a variable diameter \(\frac{3}{2}\) (2x + 1). Find the rate of change of its volume with respect to x.
Solution.
The volume of a sphere (V) with radius (r) is given by
V = \(\frac{4}{3}\) πr3
It is given that, Diameter = \(\frac{3}{2}\) (2x + 1)
⇒ r = \(\frac{3}{4}\) (2x + 1)
∴ V = \(\frac{4}{3} \pi\left(\frac{3}{4}\right)^{3}(2 x+1)^{3}\)
= \(\frac{9}{16} \pi(2 x+1)^{3}\)
Hence, the rate of change of volume with respect to x is
\(\frac{d V}{d x}=\frac{9}{16} \pi \frac{d}{d x}(2 x+1)\)= \(\frac{9}{16} \pi \times 3(2 x+1)^{2} \times 2\)
= \(\frac{27}{8} \) π (2x + 1)2
Question 14.
Sand is pouring from a pipe at the rate of 12 cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?
Solution.
The volume of a cone (V) with radius (r) and height (h) is given by V = \(\frac{1}{3}\) πr2h
It is given that, h = \(\frac{1}{6}\) r
⇒ r = 6h
⇒ V = \(\frac{1}{3}\) π(6h)2 h
= 12 πh3
The rate of change of volume with respect to time (t) is given by
\(\frac{d V}{d t}\) = 12π \(\frac{d}{d h}\) (h3) . \(\frac{d h}{d t}\)
= 12π (3h2) \(\frac{d h}{d t}\)
= 36πh2 \(\frac{d h}{d t}\)
It is also given that \(\frac{d V}{d t}\) = 12 cm3/ s
Therefore, when h = 4 cm, we have
12 = 36π(4)2 \(\frac{d h}{d t}\)
Hence, when the height of the sand cone is 4 cm, its height is increasing at the rate of\(\frac{1}{48 \pi}\) cm/s.
![]()
Question 15.
The total cost C(x) in rupees associated with the production of x units of an item is given by
C(x) = 0.007 x3 – 0.003 x2 + 15x + 4000.
Find the marginal cost when 17 units are produced.
Solution.
Marginal cost is the rate of change of total cost with respect to output.
Marginal cost (MC) = \(\frac{d C}{d x}\)
= 0.007 (3x2) – 0.003 (2x) + 15
= 0.021 x2 – 0.006x + 15
When x = 17, then MC = 0.021 (172) – 0.006 (17) +15
= 0.021 (289) – 0.006 (17) +15
= 6.069 – 0.102 + 15 = 20.967
Hence, when 17 units are produced, the marginal cost is ₹ 20.967.
Question 16.
The total revenue in rupees received from the sale of x units of a product is given by R(x) = 13x2 + 26x + 15. Find the marginal revenue when x = 7.
Solution.
Marginal revenue is the rate of change of total revenue with respect to the number of units sold.
Marginal Revenue (MR) = \(\frac{d R}{d x}\)
= 13(2x) + 26
= 26x + 26
When x = 7, then MR = 26(7) + 26
= 182 + 26 = 208
Hence, the required marginal revenue is ₹ 208.
![]()
Direction (17 – 18):
Choose the correct answer.
Question 17.
The rate of change of the area of a circle with respect to its radius r at r = 6 cm is
(A) 10π
(B) 12π
(C) 8π
(D) 11π
Solution.
The area of a circle (A) with radius (r) is given by
A = πr2
Therefore, the rate of change of the area with respect to its radius r is
\(\frac{d A}{d r}\) = \(\frac{d}{d r}\) (πr2) = 2πr
∴ When r = 6 cm
⇒ \(\frac{d A}{d r}\) = 2π × 6 = 12π cm2/s
Hence, the required rate of change of the area of a circle is 12π cm2/s.
The correct answer is (B).
![]()
Question 18.
The total revenue in rupees received from the sale of x units of a product is given by R(x) = 3x2 + 36x + 5. The marginal revenue, when x = 15, is
(A) 116
(B) 96
(C) 90
(D) 126
Solution.
Marginal revenue is the rate of change of total revenue with respect to the number of units sold.
∴ Marginal Revenue (MR) = \(\frac{d R}{d x}\)
= 3(2x) + 36 = 6x + 36
∴ When x = 15, then MR = 6(15) + 36 = 90 + 36 = 126
Hence, the required marginal revenue is ₹ 126.
The correct answer is (D).
