PSEB 12th Class Maths Solutions Chapter 6 Application of Derivatives Miscellaneous Exercise

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 6 Application of Derivatives Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 6 Application of Derivatives Miscellaneous Exercise

Question 1.
Using differentials, find the approximate value of each of the following:
Solution.
(a) \(\left(\frac{17}{81}\right)^{\frac{1}{4}}\)
Solution.
Consider y = \(x^{\frac{1}{4}}\).

Let x = \(\frac{16}{81}\) and ∆x = \(\frac{1}{81}\).

Then, ∆y = (x + ∆x)^{\(\frac{1}{4}\)} – x^{\(\frac{1}{4}\)}

= \(\left(\frac{17}{81}\right)^{\frac{1}{4}}-\left(\frac{16}{81}\right)^{\frac{1}{4}}\)

= \(\left(\frac{17}{81}\right)^{\frac{1}{4}}-\frac{2}{3}\)

∴ \(\left(\frac{17}{81}\right)^{\frac{1}{4}}\) = \(\frac{2}{3}\) + ∆y

Now, dy is approximately equal to ∆y and is given by

dy = \(\left(\frac{d y}{d x}\right) \Delta x=\frac{1}{4(x)^{\frac{3}{4}}}(\Delta x)\)

= \(\frac{1}{4\left(\frac{16}{81}\right)^{\frac{3}{4}}}\left(\frac{1}{81}\right)=\frac{27}{4 \times 8} \times \frac{1}{81}=\frac{1}{32 \times 3}=\frac{1}{96}\) = 0.010

Hence, the approximate value of \(\left(\frac{17}{81}\right)^{\frac{1}{4}}\) is \(\frac{2}{3}\) + 0.010
= 0.667 + 0.010 = 0.677.

(b) Consider y = \(x^{-\frac{1}{5}}\).
Let x = 32 and ∆x = 1.
Then, ∆y = (x + ∆x)^{\(-\frac{1}{5}\)} – x^{\(-\frac{1}{5}\)}

= (33)^{\(-\frac{1}{5}\)} – (32)^{\(-\frac{1}{5}\)}

= (33)^{\(-\frac{1}{5}\)} – \(\frac{1}{2}\)
∴ (33)^{\(-\frac{1}{5}\)} = \(\frac{1}{2}\) + ∆y

Now, dy is approximately equal to ∆y and is given by
dy = \(\left(\frac{d y}{d x}\right) \Delta x=\frac{-1}{5(x)^{\frac{6}{5}}}(\Delta x)\) (As y = x^{\(-\frac{1}{5}\)})

= \(\frac{-1}{5(2)^{6}}(1)=-\frac{1}{320}\) = – 0.003.

Hence, the approximate value of (33)^{\(-\frac{1}{5}\)}
= \(\frac{1}{2}\) + (- 0.003) = 0.5 – 0.003 = 0.497.

Question 2.
Show that the function given by f(x) = \(\frac{\log x}{x}\) maximum at x = e.
Solution.
The given function is f(x) = \(\frac{\log x}{x}\)

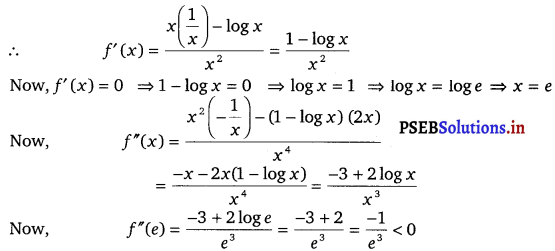
Therefore, by second derivative test, f is the maximum at x = e.

Question 3.
The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast s the area decreasing when two equal sides are equal to the base?
Solution.

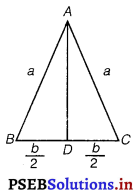
Let ∆ ABC be isosceles, where BC is the base of fixed length b.
Let the length of the two equal sides of ∆ABC be a.
Draw AD ⊥ BC

Now, in ∆ADC, by applying the Pythagoras theorem, we have

AD = \(\sqrt{a^{2}-\frac{b^{2}}{4}}\)

:. Area of triangle (A) = \(\frac{1}{2} b \sqrt{a^{2}-\frac{b^{2}}{4}}\)

The rate of change of the area with respect to time (t) is given by

\(\frac{d A}{d t}=\frac{1}{2} b \cdot \frac{2 a}{2 \sqrt{a^{2}-\frac{b^{2}}{4}}} \cdot \frac{d a}{d t}=\frac{a b}{\sqrt{4 a^{2}-b^{2}}} \cdot \frac{d a}{d t}\)

It is given that the two equal sides of the triangle are decreasing at the rate of 3 cm per second.

∴ \(\frac{d a}{d t}\) = – 3 cm/s (Negative sign shows for decreasing)

∴\(\frac{d A}{d t}=\frac{-3 b}{\sqrt{4 a^{2}-b^{2}}} \mathrm{~cm}^{2} / \mathrm{s}\) cm² / s

When a = b, we have \(\frac{d A}{d t}=\frac{-3 b^{2}}{\sqrt{4 b^{2}-b^{2}}}=\frac{-3 b^{2}}{\sqrt{3 b^{2}}}\) = √3b cm² / s
Hence, if the two equal sides are equal to the base, then the area of the triangle ¡s decreasing at the rate of √3 db cm²/s.

Question 4.
Find the equation of the normal to curve y² = 4x at the point (1, 2).
Solution.
The equation of the given curve is y² = 4x.
On differentiating w.r.t. x, we get
2y \(\frac{d y}{d x}\) = 4

⇒ \(\frac{d y}{d x}\) = \(\frac{4}{2 y}=\frac{2}{y}\)

Slope of the tangent at (1, 2) is \(\left(\frac{d y}{d x}\right)_{(1,2)}=\frac{2}{2}\) = 1
and slope of the normal at the point (1, 2) is = \(\frac{-1}{1}\) = – 1.
∴ Equation of the normal at (1, 2) is
y – 2 = – 1(x – 1)
⇒ y – 2 = – x + 1
⇒ x + y – 3 = 0.

Question 5.
Show that the normal at any point 0 to the curve x = a cos0 + a0 sin0, y = a sin0 – a0 cos0 is at a constant distance from the origin.
Solution.
The given curve is x = a cos θ + a θ sin θ, y = a sin θ – a θ cos θ
On differentiating w.r.t. θ, we get dx
\(\frac{d x}{d \theta}\) = – a sin θ + a sin θ + a θ cos θ
= a θ cos θ

and \(\frac{d y}{d \theta}\) = a cos θ – a cos θ + a θ sin θ
= a θ sin θ

Slope of the tangent at θ,

\(\frac{d y}{d x}=\frac{d y}{d \theta} \cdot \frac{d \theta}{d x}=\frac{a \theta \sin \theta}{a \theta \cos \theta}\) = tan θ

∴ Slope of the normal at θ is \(\frac{1}{\tan \theta}\) = – cot θ.

The equation of the normal at a given point (x, y) is given by
y – a sin θ + a θ cos θ = – \(\frac{1}{\tan \theta}\) (x – a cos θ – a θ sin θ)

⇒ y sin θ – a sin2 θ + a θ sin θ cos θ = – x cos θ + a cos2 θ + a θ sin θ cos θ
⇒ x cos θ + y sin θ – a (sin² θ + cos² θ) = 0
⇒ x cos θ + y sin θ – a = 0
Now, the perpendicular distance of the normal from the origin is \(\frac{|-a|}{\sqrt{\cos ^{2} \theta+\sin ^{2} \theta}}=\frac{|-a|}{\sqrt{1}}=|-a|\), which is independent of θ.
Hence, the perpendicular distance of the normal from the origin is constant.

Question 6.
Find the intervals in which the function f given by f(x) = \(\frac{4 \sin x-2 x-x \cos x}{2+\cos x}\) is
(i) strictly increasing
(ii) strictly decreasing
Solution.
Given, f(x) = \(\frac{4 \sin x-2 x-x \cos x}{2+\cos x}\)

Now, f'(x) = 0
⇒ cos x = 0 or cos x = 4
But, cos x ≠ 4
∴ cos x = 0
⇒ x = \(\frac{\pi}{2}, \frac{3 \pi}{2}\)
Now, x = \(\frac{\pi}{2}\) and x = \(\frac{3 \pi}{2}\) divides (0, 2π) into three disjoint intervals i.e.,
(0, \(\frac{\pi}{2}\)), (\(\frac{\pi}{2}, \frac{3 \pi}{2}\)), and (\(\frac{3 \pi}{2}\), 2π)

In intervals (0, \(\frac{\pi}{2}\)) and (\(\frac{3 \pi}{2}\), 2π), f'(x) > 0.

Thus, f(x) is increasing for 0 < x < \(\frac{x}{2}\) and \(\frac{3 \pi}{2}\) < x < 2π.
In the interval \(\frac{\pi}{2}, \frac{3 \pi}{2}\), f'(x) < 0.
Thus, f(x) is decreasing for \(\frac{\pi}{2}\) < x < \(\frac{3 \pi}{2}\).

Question 7.
Find the intervals in which the function f given by f(x) = x³ + \(\frac{1}{x^{3}}\), x ≠ 0 is
(i) increasing
(ii) decreasing
Solution.
f(x) = x³ + \(\frac{1}{x^{3}}\)

∴ f'(x) = 3x² – \(\frac{3}{x^{4}}=\frac{3 x^{6}-3}{x^{4}}\)

Then, f’(x) = 0 = 3x⁶ – 3 = 0
⇒ x⁶ = 1
⇒ x = ± 1
Now, the points x = 1 and x = – 1 divide the real line into three disornt intervals i.e., (- ∞, – 1), (- 1, 1), and (1, ∞).
In intervals (- ∞, – 1) and (1, ∞) i.e., when x < – 1 and x > 1, f’(x) > 0.
Thus, when x < – 1 and x > 1, f is increasing.
In interval (- 1, 1) i.e., when – 1 < x < 1, f’(x) < 0.
Thus, when – 1 < x < 1, f is decreasing.

Question 8.
Find the maximum area of an isosceles triangle inscribed in the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 with Its vertex at one end of the major
Solution.

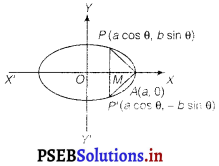
A = area of isosceles ∆ APP’
= \(\frac{1}{2}\) . PP’ . AM

= \(\frac{1}{2}\) ab (2b sin θ) (a – a cos θ)

= ab (sin θ – \(\frac{1}{2}\) sin 2θ)

Differentiating w.r.t. θ, we get
\(\frac{d A}{d \theta}\) = ab (cos θ – cos 2θ)

For maxima and minima,
\(\frac{d A}{d \theta}\) = 0

∴ ab(cos θ – cos 2θ) = 0
⇒ cos 2θ = cos θ
⇒ 2θ = 2π – θ
⇒ θ = \(\frac{2 \pi}{3}\)

Now, \(\frac{d^{2} A}{d \theta^{2}}\) = ab(- sin θ + 2 sin 2θ)

At θ = \(\frac{2 \pi}{3}\),

\(\frac{d^{2} A}{d \theta^{2}}\) = ab \(\left(-\sin \frac{2 \pi}{3}+2 \sin \frac{4 \pi}{3}\right)\)

= ab \(\left[-\left(\frac{\sqrt{3}}{2}\right)+2\left(-\frac{\sqrt{3}}{2}\right)\right]\)

= ab \(\left(-\frac{\sqrt{3}}{2}-\frac{2 \sqrt{3}}{2}\right)=\frac{-3 \sqrt{3}}{2}\) ab < 0

⇒ A is maximum, when θ = \(\frac{2 \pi}{3}\) = 120°

Maximum value of A = ab(sin 120° – \(\frac{1}{2}\) sin 240°)
= ab \(\left[\frac{\sqrt{3}}{2}-\frac{1}{2}\left(-\frac{\sqrt{3}}{2}\right)\right]=\frac{3 \sqrt{3}}{4} a b\)

Thus, rnaximum area o the isosceles triangle is \(\frac{3 \sqrt{3}}{4} a b\) ab sq. unit.

Question 9.
A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth in 2 m and volume is 8 m³. If building of tank costs ₹ 70 per sq m for the base and ₹ 45 per sq metre for sides. What is the cost of least expensive tank?
Solution.
Let l, b and h represent the length, breadth and height of the tank, respectively.
Then, we have height (ft) = 2 m
∴ Volume of the tank = 8 m³
⇒ Volume of the tank = l × b × h
⇒ 8 = l × b × 2
⇒ lb = 4
⇒ b = \(\frac{4}{l}\)
Now, area of the base = lb = 4
Area of the 4 walls (A) = 2h (l + b)
∴ A = 4 (l + \(\frac{4}{l}\))
⇒ \(\frac{d A}{d l}=4\left(1-\frac{4}{l^{2}}\right)\)
However, the length cannot be negative.
Therefore, we have l = 4
∴ b = \(\frac{4}{l}=\frac{4}{2}\) = 2

Now, \(\frac{d^{2} A}{d l^{2}}=\frac{32}{l^{3}}\)

when l = 2, then \(\frac{d^{2} A}{d l^{2}}=\frac{32}{8}\) = 4 > 0

Thus, by second derivative test, the area is the minimum when l = 2.
We have l = b = h = 2
∴ Cost of building the base = ₹ 70 × (lb)
= ₹ 70 (4) = ₹ 280
Cost of building the walls = ₹ 2h (l + b) × 45
= ₹ 90 (2) (2 + 2)
= ₹ 8 (90) = ₹ 720
Required total cost = ₹ 280 + 720 = ₹ 1000
Hence, the total cost of the tank will be ₹ 1000.

Question 10.
The sum of the perimeter of a circle and square is k, where k is some constant. Prove that the sum of their areas is least when the side of square is double the radius of the circle.
Solution.
Let x be the radius of the circle and y be the side of the square
Circumference of the circle = 2πx
Perimeter of square = 4y
Sum of perimeters of circle and square = 2πx + 4y = k ……………(i)
Area of circle = πx²
Area of square = y²
Sum of areas of circle and square = πx² + y² …………..(ii)
From Eq. (i),
y = \(\frac{k-2 \pi x}{4}\) ……………..(iii)

Question 11.
A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 m. Find the dimensions of the window to admit maximum light through the whole opening.
Solution.

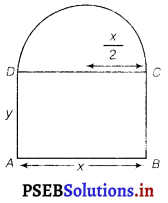
Let x and y be the length and breadth of the rectangular window.
Then, radius of the semicircular opening = \(\frac{x}{2}\)
It is given that the perimeter of the window is 10 m.
∴ x + 2y + \(\frac{\pi x}{2}\) = 10

⇒ (x + \(\frac{\pi}{2}\)) + 2y = 10

⇒ 2y = 10 – x (1 + \(\frac{\pi}{2}\))

⇒ y = 5 – x (\(\frac{1}{2}+\frac{\pi}{4}\))

∴ Area of the window (A) is given by

Therefore, by second derivative test, the area is the maximum when length x = \(\frac{20}{\pi+4}\) m.

y = \(5-\frac{20}{\pi+4}\left(\frac{2+\pi}{4}\right)=5-\frac{5(2+\pi)}{\pi+4}=\frac{10}{\pi+4} \mathrm{~m}\)

Hence, the required dimensions of the window to admit maximum light is given by length = \(\frac{20}{\pi+4}\) m and breadth = \(\frac{10}{\pi+4}\) m.

Question 12.
A point on the hypotenuse of a triangle is at distance a and b from the sides of the triangle. Show that the maximum length of the hypotenuse is \(\left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)^{\frac{3}{2}}\).
Solution.
Let ∆ ABC be right angled at B.
Let AB = x and BC = y.
Let P be a point on the hypotenuse of the triangle such that P is at a distance of a and b from the sides AB and BC respectively.

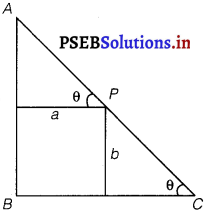
Let ∠C = θ.
We have, AC = \(\sqrt{x^{2}+y^{2}}\)
Now, PC = b cosec θ and, AP = a sec θ
∴ AC = AP + PC
⇒ AC = b cosec θ + a sec θ ……………. (i)

∴ \(\frac{d(A C)}{d \theta}\) = – cosec θ cot θ + a sec θ tan θ

∴ \(\frac{d(A C)}{d \theta}\) = 0

⇒ a sec θ tan θ = cosec θ cot θ

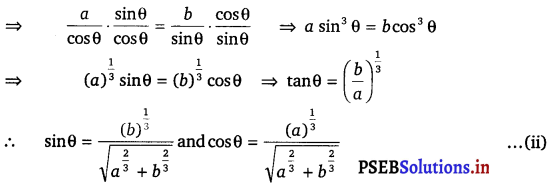
It can be clearly shown that \(\frac{d^{2}(A C)}{d \theta^{2}}\) < 0 when tan θ = \(\left(\frac{b}{a}\right)^{\frac{1}{3}}\).

Therefore, by second derivative test, the length of the hypotenuse is the tan θ = \(\left(\frac{b}{a}\right)^{\frac{1}{3}}\).

Now, when tan θ = \(\left(\frac{b}{a}\right)^{\frac{1}{3}}\), then we have

AC = \(\frac{b \sqrt{a^{\frac{2}{3}}}+b^{\frac{2}{3}}}{b^{\frac{1}{3}}}+\frac{a \sqrt{a^{\frac{2}{3}}}+b^{\frac{2}{3}}}{a^{\frac{1}{3}}}\) [Using Eqs. (i) and (ii)]

= \(\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}\left(b^{\frac{2}{3}}+a^{\frac{2}{3}}\right)=\left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)^{\frac{3}{2}}\)

Hence, the maximum length of the hypotenuse is \(\left(a^{\frac{2}{3}}+b^{\frac{2}{3}}\right)^{\frac{3}{2}}\).

Question 13.
Find the points at which the function f given by f(x) = (x – 2)⁴ (x + 1)³ has –
(i) local maxima
(ii) local minima
(iii) point of inflexion
Solution.
The given function is f(x) = (x – 2)⁴ (x + 1)³
∴ f'(x) = 4 (x – 2)³ (x + 1)³ + 3(x + 1)² (x – 2)⁴
= (x – 2)³ (x +1)² [4(x + 1) + 3(x – 2)]
= (x – 2)³ (x + 1)² (7x – 2)
f'(x) = 0
⇒ x = – 1 and x = \(\frac{2}{7}\) or x = 2
Now, for values of x close to \(\frac{2}{7}\) and to the left of \(\frac{2}{7}\), f'(x) > 0.

Also, for values of x close to \(\frac{2}{7}\) and to the right of \(\frac{2}{7}\), f'(x) < 0.

Thus, x = \(\frac{2}{7}\) is the point of local maxima.
Now, for values of x close to 2 and to the left of 2, f'(x) < 0. Also, for values of x close to 2 and to the right of 2, f'(x) > 0.
Thus, x = 2 is the point of local minima.
Now, as the value of x varies through – 1, f (x) does not change its sign.
Thus, x = – 1 is the point of inflexion.

Question 14.
Find the absolute maximum and minimum values of the function f’given by f(x) = cos² x + sin x, x ∈ [0, π].
Solution.
Given, f(x) = cos² x + sin x
∴ f'(x) = 2 cos x (- sin x) + cos x = – 2 sin x cos x + cos x
Now, f’ (x) = 0
⇒ 2 sin x cos x = cos x
⇒ 2 sin x cos x – cos x = 0
⇒ cos x (2 sin x – 1) = 0
⇒ sin x = – or cos x = 0
⇒ x = \(\frac{\pi}{6}\) or \(\frac{\pi}{2}\) as x ∈ [0, π]
Now, evaluating the value of f at critical points x = \(\frac{\pi}{2}\) and x = \(\frac{\pi}{6}\) and at
the end points of the interval [0, π] (i.e., at x = 0 and x = π), we have

f(\(\frac{\pi}{6}\)) = cos² \(\frac{\pi}{6}\) + sin \(\frac{\pi}{6}\)
= \(\left(\frac{\sqrt{3}}{2}\right)^{2}+\frac{1}{2}=\frac{5}{4}\)

f(0) = cos² 0 + sin 0
= 1 + 0 = 1

f(π) = cos² π + sin π
= (- 1)² + 0 = 1

f(\(\frac{\pi}{2}\)) = cos² \(\frac{\pi}{2}\) + sin \(\frac{\pi}{2}\)
= 0 + 1 = 1

Hence, the absolute maximum value of f is \(\frac{5}{4}\) occurring at x = \(\frac{\pi}{6}\) and the absolute minimum value of f is 1 occurring at x = 0, \(\frac{\pi}{2}\) and π.

Question 15.
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r, is -.
Solution.

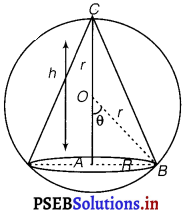
Let R be the radius and h be the height of cone.
∴OA = h – r
In ∆OAB, r² = R² + (h – r)²
⇒ r² = R² + h² + r² – 2rh
⇒ R² = 2rh – h²
The volume V of the cone is given by V = \(\frac{1}{3}\) πR²h
= \(\frac{1}{3}\) πh (2rh – h²)

= \(\frac{1}{3}\) π (2rh² – h³)

On differentiating w.r.t. h, we get
\(\frac{d V}{d h}\) = \(\frac{1}{3}\) π (4rh – 3h²)

For maximum or minimum put \(\frac{d V}{d h}\) = 0
⇒ 4rh = 3h²
⇒ 4r = 3h
∴ h = \(\frac{4 r}{3}\) (h ≠ 0)

Now, \(\frac{d^{2} V}{d h^{2}}\) = \(\frac{1}{3}\) π (4r – 6h)

At h = \(\frac{4 r}{3}\),

\(\left(\frac{d^{2} V}{d h^{2}}\right)_{h=\frac{4 r}{3}}\) = \(\frac{1}{3}\) π (4r – 6 × \(\frac{4 r}{3}\))

= \(\frac{pi}{3}\) (4r – 8r) = \(\frac{-4 r \pi}{3}\) < 0 ⇒ V is maximum when h = \(\frac{4 r}{3}\) Hence, volume of the cone is maximum when h = \(\frac{4 r}{3}\), which is the altitude of cone. Question 16. Let f be a function defined on [a, b] such that f'(x) > 0, for all x ∈ (a, b). Then prove that f is an increasing function on (a, b).
Solution.
Given, f'(x) > 0 on (a, b)
f is a differentiable function on (a, b).
Also, every differentiable function is continuous, therefore, f is continuous on (a, b).
Let x₁, x₂ ∈ [a, b] and x₂ > x₁; then by LMV theorem, there exist c ∈ [a, b] such that

f'(c) = \(\frac{f\left(x_{2}\right)-f\left(x_{1}\right)}{x_{2}-x_{1}}\)
⇒ f(x₂) – f(x₁) = (x₂ – x₁) f'(c)
⇒ f(x₂) – f(x₁) > 0 as x₂ > x₁ and f'(x) > 0
⇒ f(x₂) > f(x₁)
For x₁ < x₂
⇒ f(x₁) < f(x₂)
Hence, f is an increasing function on (a, b).

Question 17.
Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R, is . Also, find the maximum volume.
Solution.

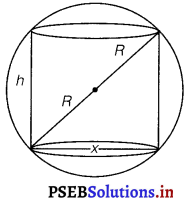
Radius of the sphere = R
Let h be the height and x be the diameter of the base of the inscribed cylinder Then.
h² + x² = (2R)²
⇒ h² + x² = 4R² …………(i)
Volume of the cylinder = π (radius)² × height

⇒ V = π (\(\frac{x}{2}\))² . h
= \(\frac{1}{4}\) πx²h
⇒ V = \(\frac{1}{4}\) πh(4R² – h²) …………(ii)
[From Eq. (i), x² = 4R² – h²]

⇒ V = πR²h – \(\frac{1}{4}\) πh³
On differentiating w.r.t h, we get
\(\frac{d V}{d h}\) = πR²h – \(\frac{3}{4}\) πh²
= π (R² – \(\frac{3}{4}\) h²)

Put \(\frac{d V}{d h}\) = 0
⇒ R² = \(\frac{3}{4}\) h²
⇒ h = \(\frac{2 R}{\sqrt{3}}\)

Thus, volume of the cylinder is maximum when h = \(\frac{2 R}{\sqrt{3}}\).

Question 18.
Show that height of the cylinder of greatest volume which can be inscribed in a circular cone of height h and having
semi-vertical angle a is one-third that of one cone and the
greatest volume of cylinder Is ida3 tan2 a.
Solution.

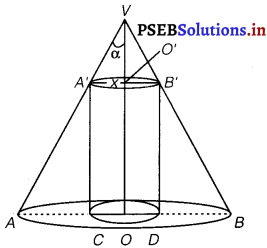
Let VAR be the cone of height h, semi-vertical angle a and let x be the radius of the base of the cylinder A’ B’ DC which is inscribed in the cone VAB.
Then, OO’ is the height of the cylinder = VO – VO’ = h – x cot α
Volume of the cylinder,
V = πx² (h – x cot α) ………………(i)
On differentiating w.r.t. x, we get
\(\frac{d V}{d x}\) = 2πrh – 3πx² cot α
For maxima or minima put \(\frac{d V}{d x}=\)= 0
⇒ 2πxh – 3πx² cot α = 0

⇒ x = \(\frac{2 h}{3}\) tan α (∵ x ≠ 0)

Now, \(\frac{d^{2} V}{d x^{2}}\) = 2πh – 6π x cot α

At x= \(\frac{2 h}{3}\) tan α,

\(\frac{d^{2} V}{d x^{2}}\) = π (2h – 4h) = – 2πh < 0

Now, OO’ = h – x cot α = h – \(\frac{2 h}{3}\) = \(\frac{h}{3}\)

∴ The maximum volume of the cylinder is V = π (\(\frac{2 h}{3}\) tan α)² (h – \(\frac{2 h}{3}\))

= \(\frac{4}{27}\) πh³ tan² α.

Direction (19 – 24):
Choose the correct answer.

Question 19.
A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic meter per hour. Then the depth of the wheat is increasing at the rate of
(A) 1 m/h
(B) 0.1 m/h
(C) 1.1 m/h
(D) 0.5 m/h
Solution.
Let r be the radius of the cylinder.
Then, volume (V) of the cylinder is given by,
V = π (radius)² × height
= π (10)² h (radius = 10 m)
= 100 πh
On differentiating w.r.t. t, we get
\(\frac{d V}{d t}\) = 100 π \(\frac{d h}{d t}\)
The tank is being filled with wheat at the rate of 314 cubic metres per hour.
\(\frac{d V}{d t}\) = 314 m³/h

Thus, we have
314 = 100π \(\frac{d h}{d t}\)

⇒ \(\frac{d h}{d t}\) = \(\frac{314}{100(3.14)}=\frac{314}{314}\) = 1

Hence, the depth of wheat is increasing at the rate of 1 m / h.
The correct answer is (A).

Question 20.
The slope of the tangent to the curve x = t² + 3t – 8, y = 2t² – 2t – 5 at the point (2, – 1) is
(A) \(\frac{22}{7}\)

(B) \(\frac{6}{7}\)

(C) \(\frac{7}{6}\)

(D) \(\frac{-6}{7}\)
Solution.
The given curve is x = t² + 3t – 8 and y = 2t² – 2t – 5
∴ \(\frac{d x}{d t}\) = 2t + 3 and

\(\frac{d y}{d t}\) =4t – 2

∴ \(\frac{d y}{d x}=\frac{d y}{d t} \cdot \frac{d t}{d x}=\frac{4 t-2}{2 t+3}\)

The given point is (2, – 1)
At x = 2, we have r2+3r-8=2
⇒ t² + 3t – 10 = 0
⇒ (t – 2) (t + 5) = 0
⇒ t = 2 or t = – 5
At y = – 1, we have
⇒ 2t² – 2t – 4 = 0
⇒ 2 (t² – t – 2) = 0
⇒ t = 2 or t = – 1
The common value oft is 2.
Hence, the slope of the tangent to the given curve at point (2, – 1) is

\(\left[\frac{d y}{d x}\right]_{t=2}=\frac{4(2)-2}{2(2)+3}=\frac{8-2}{4+3}=\frac{6}{7}\)
The correct answer is (B).

Question 21.
The line y = mx + 1 is a tangent to the curve y2 = 4# if the value of m is
(A) 1
(B) 2
(C) 3
(D) \(\frac{1}{2}\)
Solution.
The equation of the tangent to the given curve is y = mx + 1.
Now, substituting y = mx + 1 in y² = 4x, we get
⇒ (mx + 1)² = 4x
⇒ m²x² +1 + 2mx – 4x = 0
⇒ m²x² + x (2m – 4) + 1 = 0 …………….(i)
Since a tangent touches the curve at one point, the roots of equation (i) must be equal.
Therefore, we have
Discriminant = 0
⇒ (2m – 4)² – 4(m²) (1) = 0
⇒ 4m² + 16 – 16m – 4m² = 0
⇒ 16 – 16m = 0
⇒ m = 1
Hence, the required value of m is 1.
The correct answer is A.

Question 22.
The normal at the point (1, 1) on the curve 2y + x² = 3 is
(A) x + y = 0
(B) x – y = 0
(C) x + y + 1 = 0
(D) x – y = 0
Solution.
The equation of the given curve is 2y + x² = 3

\(\frac{2 d y}{d x}\) + 2x = 0

\(\frac{d y}{d x}\) = – x

Slope of the normal to the given curve at point (1, 1) is \(\frac{-1}{\left[\frac{d y}{d x}\right]_{(1,1)}}=\frac{-1}{-1}\) = 1
Hence, the equation of the normal to the given curve at (1, 1) is given as
⇒ y – 1 = 1 (x – 1)
⇒ y – 1 = x – 1
⇒ x – y = 0
The correct answer is (B).

Question 23.
The normal to the curve x² = 4y passing (1, 2) is
(A) x + y = 3
(B) x – y = 3
(C) x + y = 1
(D) x – y = 1
Solution.
The equation of the given curve is x = 4y
Differentiating w.r.t x, we get
2x = 4 \(\frac{d y}{d x}\)

∴ \(\frac{d y}{d x}=\frac{2 x}{4}=\frac{x}{2}\) = slope of the tangent
∴Slope of the normal = (- 1) / slope of tangent
∴ Equation of normal at (x₁, y₁) is
y – y₁ = (x – x₁) ……………..(i)
It passes through (1, 2), therefore
2 – y₁ = – \(\frac{2}{x_{1}}\) (1 – x₁)
⇒ 2x₁ – x₁y₁ = – 2 + 2x₁
x₁y₁ = 2
or y₁ = \(\frac{2}{x_{1}}\) …………(ii)
The point (x₁, y₁) lies on x² = 4y
x₁² = 4y₁ ……………(iii)
From Eqs. (i) and (iii), we get
x₁² = 4 . \(\frac{2}{x_{1}}\)
∴ x₁³ = 8
x₁ = 2
From Eq. (iii), 4 = 4y₁
∴ y₁ = 1
Putting these values in Eq. (i), we get
y – 1 = – \(\frac{2}{24}\) (x – 2)
y – 1 = – x + 2
⇒ x + y = 3
The correct answer is (A).

Question 24.
The points on the curve 9y² = x³, where the normal to the curve makes equal intercepts with the axes are
(A) (4, ± \(\frac{8}{3}\))

(B) (4, – \(\frac{8}{3}\))

(C) (4, ± \(\frac{3}{8}\))

(D)(± 4, \(\frac{3}{8}\))
Solution.
The equation of the given curve is 9y² = x³
Differentiating w.r.t. x, we get
18 y \(\text { dy }\) = 3x²

⇒ \(\frac{d y}{d x}=\frac{x^{2}}{6 y}\)

Let P(x₁, y₁) be the point where normal is drawn
Slope of tangent = \(\frac{x_{1}^{2}}{6 y_{1}}\)

∴ Slope of normal = \(\frac{6 y_{1}}{x_{1}^{2}}\)

Normal make equal intercepts on the curve
∴ Its slope = ± 1
– \(\frac{6 y_{1}}{x_{1}^{2}}\) = ± 1
⇒ 6y₁ = ± x₁² ……………..(i)
(x₁, y₁)lies on the curve 9y² = x³
⇒ 9y₁² = x₁³ …………..(ii)
Taking +ve sign, eliminating y₁ from Eq. (1) and Eq. (ii),
9 \(\left(\frac{x_{1}^{2}}{6}\right)^{2}\) = x₁³
⇒ \(\frac{9 x_{1}^{4}}{36}\) = x₁³
⇒ x₁ = 4
From Eq. (i),
y₁ = ± \(\frac{x_{1}^{2}}{6}=\pm \frac{16}{6}\)[Putting x = 4]
= ± \(\frac{8}{3}\)
∴ The point P is (4, ± \(\frac{8}{3}\))
The correct answer is (A).