PSEB 12th Class Maths Solutions Chapter 7 Integrals Ex 7.10

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 7 Integrals Ex 7.10 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 7 Integrals Ex 7.10

Direction (1 – 8): Evaluate the integrals using substitution.

Question 1.
\(\int_{0}^{1} \frac{x}{x^{2}+1}\) dx
Solution.
\(\int_{0}^{1} \frac{x}{x^{2}+1}\) dx
Let x² + 1 = t
⇒ 2x dx = dt
When x = 0, t = 1 and when x = 1, t = 2
∴ \(\int_{0}^{1} \frac{x}{x^{2}+1}\) dx = \(\frac{1}{2} \int_{1}^{2} \frac{d t}{t}\)

= \(\frac{1}{2}[\log |t|]_{1}^{2}\)

= \(\frac{1}{2}\) [log 2 – log 1]

= \(\frac{1}{2}\) log 2.

Question 2.
\(\int_{0}^{\frac{\pi}{2}} \sqrt{\sin \phi} \cos ^{5} \phi d \phi\)
Solution.
Let I = \(\int_{0}^{\frac{\pi}{2}} \sqrt{\sin \phi} \cos ^{5} \phi d \phi=\int_{0}^{\frac{\pi}{2}} \sqrt{\sin \phi} \cos ^{4} \phi \cos \phi d \phi\)

Also let sin Φ = t
⇒ cos Φ dΦ = dt
when, Φ = 0, t = 0 and
when Φ = \(\frac{\pi}{2}\), t = 1
∴ I = \(\int_{0}^{1}\) √t (1 – t²)² dt

Question 3.
\(\int_{0}^{1} \sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right)\) dx
Solution.
Let I = \(\int_{0}^{1} \sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right)\) dx
Also, let x = tan θ
⇒ dx = sec² θ dθ
when x = 0, θ = 0 and when x = 1, θ = \(\frac{\pi}{4}\)
I = \(\int_{0}^{\frac{\pi}{4}} \sin ^{-1}\left(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right)\) sec² θ dθ

= \(\int_{0}^{\frac{\pi}{4}}\) sin^-1 (sin 2θ) sec² θ dθ

= \(\int_{0}^{\frac{\pi}{4}}\) 2θ sec² θ dθ

= 2 \(\int_{0}^{\frac{\pi}{4}}\) θ sec² θ dθ

Taking e as first function and sec² θ as second function and integrating by parts, we get
I = \(2\left[\theta \int \sec ^{2} \theta d \theta-\int\left\{\left(\frac{d}{d x}(\theta)\right) \int \sec ^{2} \theta d \theta\right\} d \theta\right]_{0}^{\frac{\pi}{4}}\)

= \(2\left[\theta \tan \theta-\int \tan \theta d \theta\right]_{0}^{\frac{\pi}{4}}=2[\theta \tan \theta+\log \mid \cos \theta]_{0}^{\frac{\pi}{4}}\)

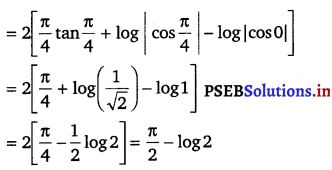
Question 4.
\(\int_{0}^{2} x \sqrt{x+2}\) (Put x + 2 = t²)
Solution.
Let I = \(\int_{0}^{2} x \sqrt{x+2}\) dx
Also let x + 2 = t²
⇒ dx = 2t dt
when x = 0, t = √2 and when x = 2, t = 2

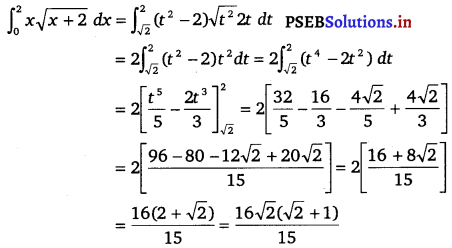
Question 5.
\(\int_{0}^{\frac{\pi}{2}} \frac{\sin x}{1+\cos ^{2} x}\) dx
Solution.
Let I = \(\int_{0}^{\frac{\pi}{2}} \frac{\sin x}{1+\cos ^{2} x}\) dx
Also, let cos x = t
⇒ – sin x dx = dt
When x = 0, t = 1 and when x = \(\frac{\pi}{2}\), t = 0
⇒ \(\int_{0}^{\frac{\pi}{2}} \frac{\sin x}{1+\cos ^{2} x}\) dx = \(-\int_{1}^{0} \frac{d t}{1+t^{2}}=-\left[\tan ^{-1} t\right]_{1}^{0}\)

= – [tan 0 – tan 1]

= – [- \(\frac{\pi}{4}\)]

= \(\frac{\pi}{4}\)

Question 6.
\(\int_{0}^{2} \frac{d x}{x+4-x^{2}}\)
Solution.
Let I = \(\int_{0}^{2} \frac{d x}{x+4-x^{2}}\)

= \(\int_{0}^{2} \frac{d x}{-\left(x^{2}-x-4\right)}\)

= \(\int_{0}^{2} \frac{d x}{-\left(x^{2}-x+\frac{1}{4}-\frac{1}{4}-4\right)}\)

= \(\int_{0}^{2} \frac{d x}{-\left[\left(x-\frac{1}{2}\right)^{2}-\frac{17}{4}\right]}\)

= \(\int_{0}^{2} \frac{d x}{\left(\frac{\sqrt{17}}{2}\right)^{2}-\left(x-\frac{1}{2}\right)^{2}}\)
Also, let x – \(\frac{1}{2}\) = t
⇒ dx = dt
When x = 0, t = – \(\frac{1}{2}\) and when x = 2,t = \(\frac{3}{2}\)

Question 7.
\(\int_{-1}^{1} \frac{d x}{x^{2}+2 x+5}\)
Solution.
Let I = \(\int_{-1}^{1} \frac{d x}{x^{2}+2 x+5}\)

= \(\int_{-1}^{1} \frac{d x}{\left(x^{2}+2 x+1\right)+4}\)

= \(\int_{-1}^{1} \frac{d x}{(x+1)^{2}+(2)^{2}}\)

Also, let x + 1 = t
⇒ dx = dt
When x = – 1, t = 0 and when x = 1, t = 2

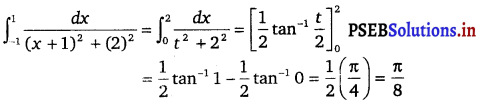
Question 8.
\(\int_{1}^{2}\left(\frac{1}{x}-\frac{1}{2 x^{2}}\right) e^{2 x}\) dx
Solution.
Let I = \(\int_{1}^{2}\left(\frac{1}{x}-\frac{1}{2 x^{2}}\right) e^{2 x}\) dx

Also, let 2x = t
⇒ 2 dx = dt
When x = 1, t = 2 and when x = 2, t = 4

Direction (9 – 10): Choose the correct answer.

Question 9.
The value of the integral \(\int_{\frac{1}{3}}^{1} \frac{\left(x-x^{3}\right)^{\frac{1}{3}}}{x^{4}}\) dx is
(A) 6
(B) 0
(C) 3
(D) 4
Solution.

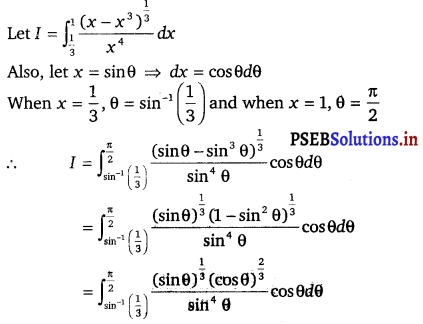
Hence, the correct answer is (A).

Question 10.
If f(x) = \(\int_{0}^{x}\) t sin t dt, then f'(x) is
(A) cos x + x sin x
(B) x sin x
(C) x cos x
(D) sin x + x cos x
Sol.
f(x) = \(\int_{0}^{x}\) t sin t dt
Integrating by parts, we get
f(x) = t \(\int_{0}^{x}\) sin t dt – \(\int_{0}^{x}\) {(\(\frac{d}{d t}\) t) ∫ sin t dt} dt
= \(\left[t(-\cos t]_{0}^{x}\right.\) – \(\int_{0}^{x}\) (- cos t) dt
= \([-t \cos t+\sin t]_{0}^{x}\)
= – x cos x + sin x
⇒ f’(x)= – [{x (- sin x)} + cos x + cos x
= x sin x – cos x + cos x
= x Sin x
Hence, the correct answer is (B).