PSEB 12th Class Maths Solutions Chapter 7 Integrals Ex 7.11

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 7 Integrals Ex 7.11 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 7 Integrals Ex 7.11

Direction (1 – 19):
By using the properties of definite integrals, evaluate the integrals.

Question 1.
\(\int_{0}^{\frac{\pi}{2}}\) cos x dx
Solution.
Let I = \(\int_{0}^{\frac{\pi}{2}}\) cos x dx ……….(i)

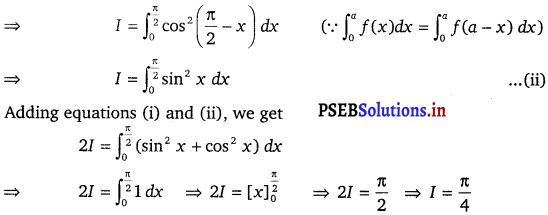
Question 2.
\(\int_{0}^{\frac{\pi}{2}} \frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}}\) dx
Solution.

Question 3.
\(\int_{0}^{\frac{\pi}{2}} \frac{\sin ^{\frac{3}{2}} x}{\sin ^{\frac{3}{2}} x+\cos ^{\frac{3}{2}} x} d x\)
Solution.

Adding equations (i) and (ii), we get

⇒ 2I = \(\int_{0}^{\frac{\pi}{2}} \frac{\sin ^{\frac{3}{2}} x+\cos ^{\frac{3}{2}} x}{\sin ^{\frac{3}{2}} x+\cos ^{\frac{3}{2}} x}\) dx

⇒ 2I = \(\int_{0}^{\frac{\pi}{2}}\) 1 dx

⇒ 2I = \([x]_{0}^{\frac{\pi}{2}}\)

⇒ 2I = \(\frac{\pi}{2}\)

⇒ I =\(\frac{\pi}{4}\)

Question 4.
\(\int_{0}^{\frac{\pi}{2}} \frac{\cos ^{5} x}{\sin ^{5} x+\cos ^{5} x}\) dx
Solution.

Question 5.
\(\int_{-5}^{5}\) |x + 2| dx
Solution.
Let I = \(\int_{-5}^{5}\) |x + 2| dx
It can be seen that (x + 2) ≤ 0 on [- 5, – 2]and (x + 2) ≥ 0 on [- 2, 5].

Question 6.
\(\int_{2}^{8}\) |x – 5| dx
Solution.
Let I = \(\int_{2}^{8}\) |x – 5| dx
It can be seen that (x – 5) ≤ 0 on [2, 5] and (x – 5) ≥ 0 on [5, 8].

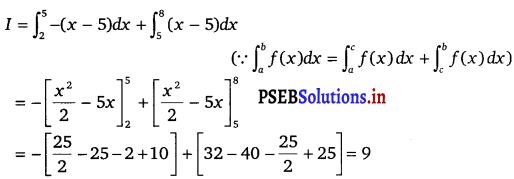
Question 7.
\(\int_{0}^{1}\) x (1 – x)ⁿ dx
Solution.
Let I = \(\int_{0}^{1}\) x (1 – x)ⁿ dx
I = \(\int_{0}^{1}\) (1 – x) (1 – (1 – x))ⁿ dx
= \(\int_{0}^{1}\) (1 – x) (x)ⁿ dx
= \(\int_{0}^{1}\) (xⁿ – xⁿ⁺¹) dx
= \(\left[\frac{x^{n+1}}{n+1}-\frac{x^{n+2}}{n+2}\right]_{0}^{1}\)

(∵ \(\int_{0}^{a}\) f(x) dx = \(\int_{0}^{a}\) f(a – x) dx

= \(\left[\frac{1}{n+1}-\frac{1}{n+2}\right]\)

= \(\frac{(n+2)-(n+1)}{(n+1)(n+2)}\)

= \(\frac{1}{(n+1)(n+2)}\)

Question 8.
\(\int_{0}^{\frac{\pi}{4}}\) log (1 + tan x) dx
Solution.

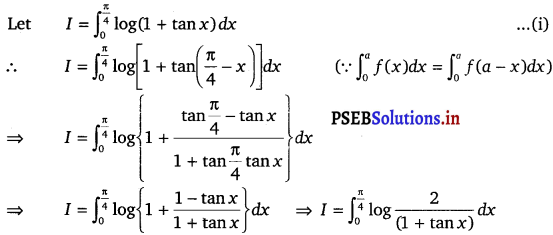
⇒ I = \(\int_{0}^{\frac{\pi}{4}}\) log 2 dx – \(\int_{0}^{\frac{\pi}{4}}\) log (1 + tan x) dx

⇒ I = \(\int_{0}^{\frac{\pi}{4}}\) log 2 dx – I [From Eq. (i)]
⇒ 2I = \([x \log 2]_{0}^{\frac{\pi}{4}}\)

⇒ 2I = \(\frac{\pi}{4}\) log 2

⇒ I = \(\frac{\pi}{8}\) log 2

Question 9.
\(\int_{0}^{2} x \sqrt{2-x}\) dx
Solution.
Let I = \(\int_{0}^{2} x \sqrt{2-x}\) dx

(∵ \(\int_{0}^{a}\) f(x) dx = \(\int_{0}^{a}\) f(a – x) dx)

I = \(\int_{0}^{2}\) (2 – x) √x dx

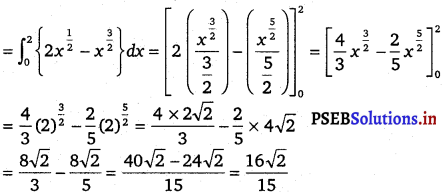
Question 10.
\(\int_{0}^{\frac{\pi}{2}}\) (2 log sin x – log sin 2x) dx
Solution.
Let I = \(\int_{0}^{\frac{\pi}{2}}\) (2 log sin x – log sin 2x) dx

⇒ I = \(\int_{0}^{\frac{\pi}{2}}\) {2 log sin x – log (2 sin x cos x)} dx

⇒ I = \(\int_{0}^{\frac{\pi}{2}}\) {2 log sin x – log sin x – log cos x – log 2} dx

⇒ I = \(\int_{0}^{\frac{\pi}{2}}\) {log sin x – log cos x – log 2}dx ……………(i)
We know that,
∵ \(\int_{0}^{a}\) f(x) dx = \(\int_{0}^{a}\) f(a – x) dx
∴ I = \(\int_{0}^{\frac{\pi}{2}}\) {log cos x – log sin x – log 2} dx …………..(ii)
Adding equations (i) and (ii), we get
2I = \(\int_{0}^{\frac{\pi}{2}}\) (log 2 – log 2) dx

⇒ 2I = – 2 log 2 \(\int_{0}^{\frac{\pi}{2}}\) 1 dx

⇒ I = – log 2 [latex]\frac{\pi}{2}[/latex]

⇒ I = \(\frac{\pi}{2}\) (- log 2)

⇒ I = \(\frac{\pi}{2}\) [log \(\frac{1}{2}\)]

⇒ I = \(\frac{\pi}{2}\) log \(\frac{1}{2}\)

Question 11.
\(\int_{\frac{2}{2}}^{\frac{\pi}{2}}\) sin² x dx
Solution.
Let I = \(\int_{\frac{2}{2}}^{\frac{\pi}{2}}\) sin² x dx
As sin² (- x) = (sin(- x))²
= (- sin x)²
= sin 2x,
therefore, sin² x is an even function.
We know that if f(x)is an even function, then
\(\int_{-a}^{a}\) f(x)dx = 2 \(\int_{0}^{a}\) f(x) dx

I = 2 \(\int_{0}^{\frac{\pi}{2}}\) sin² x dx

= 2 \(\int_{0}^{\frac{\pi}{2}} \frac{1-\cos 2 x}{2}\) dx

= \(\int_{0}^{\frac{\pi}{2}}\) (1 – cos 2x) dx

= \(\left[x-\frac{\sin 2 x}{2}\right]_{0}^{\frac{\pi}{2}}=\frac{\pi}{2}\)

Question 12.
\(\int_{0}^{\pi} \frac{x d x}{1+\sin x}\)
Solution.

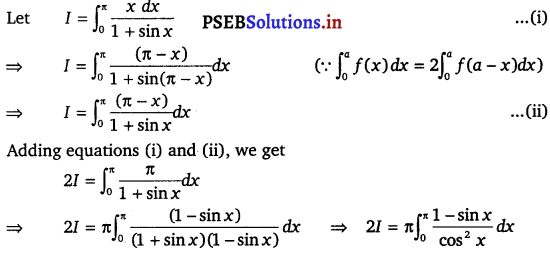
⇒ 2I = π \(\int_{0}^{\pi}\) {sec² x – tan x sec x} dx
⇒ 2I = π \([\tan x-\sec x]_{0}^{\pi}\)
⇒ 2I = π [(tan π – sec π) – (tan 0 – sec 0)
⇒ 2I = π [(0 – (- 1) – (0 – 1)]
⇒ 2I = π [2]
⇒ I = π

Question 13.
\(\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\) sin⁷ x dx
Solution.
Let I = \(\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\) sin⁷ x dx

As sin⁷ (- x) = (sin(- x))⁷
= (- sin x)⁷
= – sin⁷ x,
therefore, sin² x is an odd function.
We know that if f(x) is an odd function, then \(\int_{-a}^{a}\) f(x) dx = 0

∴ I = \(\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\) sin⁷ x dx = 0.

Question 14.
\(\int_{0}^{2 \pi}\) cos⁵ x dx
Solution.
\(\int_{0}^{2 \pi}\) cos⁵ x dx = 2 \(\int_{0}^{\pi}\) cos⁵ x dx

(∵ \(\int_{0}^{2 a}\) f(x) = 2 \(\int_{0}^{a}\) f(x), where f(2 – a))

= f(x); hence 2a = 2x

∴ cos⁵ (2x – x) = cos⁵ x
= 2 × 0 = 0
(∵ \(\int_{0}^{2 a}\) f(x) = 0, if f(2a – x) = – f(x); hence 2a = π
∴ cos^{5</sup (π – x) = – cos5 x)}

Question 15.
\(\int_{0}^{\frac{\pi}{2}} \frac{\sin x-\cos x}{1+\sin x \cos x}\) dx
Solution.
Let I = \(\int_{0}^{\frac{\pi}{2}} \frac{\sin x-\cos x}{1+\sin x \cos x}\) dx …………(i)

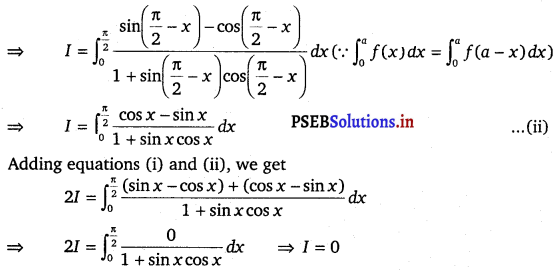
Question 16.
\(\int_{0}^{\pi}\) log (1 + cos x) dx
Solution.
Let I = \(\int_{0}^{\pi}\) log (1 + cos x) dx …………….(i)

⇒ I = \(\int_{0}^{\pi}\) log (1 + cos (π – x) dx
(∵ \(\int_{0}^{a}\) f(x) dx = \(\int_{0}^{a}\) f(a – x) dx)

⇒ I = \(\int_{0}^{\pi}\) log (1 – cos x) dx ………….(ii)

⇒ 2I = \(\int_{0}^{\pi}\) {log (1 + cos x) + log (1 – cos x)} dx

⇒ 2I = \(\int_{0}^{\pi}\) log (1 + cos² x) dx

⇒ 2I = \(\int_{0}^{\pi}\) log sin² x dx

⇒ 2I = 2 \(\int_{0}^{\pi}\) log sin x

⇒ I = \(\int_{0}^{\pi}\) log sin x dx …………..(iii)

sin (π – x) = sin x
∴ I = 2 \(\int_{0}^{\frac{\pi}{2}}\) log sin x dx ………………(iv)

⇒ I = 2 \(\int_{0}^{\frac{\pi}{2}}\) log sin (\(\frac{\pi}{2}\) – x) dx

= 2 \(\int_{0}^{\frac{\pi}{2}}\) log cos x dx ………….(v)

Adding equations (iv) and (v), we get
2I = 2 \(\int_{0}^{\frac{\pi}{2}\) (log sin x + log cos x) dx

I = \(\int_{0}^{\frac{\pi}{2}\) (log sin x + log cos x + log 2 – log 2) dx

I = \(\int_{0}^{\frac{\pi}{2}\) (log 2 sin x cos x – log 2) dx

I = \(\int_{0}^{\frac{\pi}{2}\) log sin 2x dx – \(\int_{0}^{\frac{\pi}{2}\) log 2 dx
Let 2x = t
⇒ 2 dx = dt
When x = 0, t = o and when x = \(\frac{\pi}{2}\), t = π

∴ I = log sin t dt – \(\frac{\pi}{2}\) log 2

I = \(\frac{1}{2}\) I – \(\frac{\pi}{2}\) log 2

\(\frac{I}{2}\) = – \(\frac{\pi}{2}\) log 2

⇒ I = – π log 2.

Question 17.
\(\int_{0}^{a} \frac{\sqrt{x}}{\sqrt{x}+\sqrt{a-x}}\) dx
Solution.

Question 18.
\(\int_{0}^{4}\) |x – 1| dx
Solution.
Let I = \(\int_{0}^{4}\) |x – 1| dx
It can be seen that, (x – 1) ≤ 0 when 0 ≤ x ≤ 1 and (x – 1) ≥ 0 when 1 ≤ x ≤ 4.

∴ I = \(\int_{0}^{1}\) |x – 1| dx + \(\int_{1}^{4}\) |x – 1| dx

(∵ \(\int_{a}^{b}\) f(x) = \(\int_{a}^{c}\) f(x) + \(\int_{c}^{b}\) f(x)dx)

= \(\int_{0}^{1}\) – (x – 1) dx + \(\int_{1}^{4}\) (x – 1) dx

= \(\left[x-\frac{x^{2}}{2}\right]_{0}^{1}+\left[\frac{x^{2}}{2}-x\right]_{1}^{4}\)

= \(1-\frac{1}{2}+\frac{(4)^{2}}{2}-4-\frac{1}{2}+1\)

= \(1-\frac{1}{2}+8-4-\frac{1}{2}+1\) = 5.

Question 19.
Show that \(\int_{0}^{a}\) f(x) g(x) dx = 2 \(\int_{0}^{a}\) f(x)dx if f and g are defined as
f(x) = f(a – x) and g(x) = g(a – x) = 4
Solution.
Let I = \(\int_{0}^{a}\) f(x) g(x) dx ………(i)

I = \(\int_{0}^{a}\) (a – x) g(a – x) dx

(∵ \(\int_{0}^{a}\) f(x) dx = \(\int_{0}^{a}\) f(a – x) dx)

= I = \(\int_{0}^{a}\) f(x)g (a – x) dx ……..(ii)

Adding equations (i) and (ii), we get

2I = \(\int_{0}^{a}\) {f(x) g(x) + f(x) g(a – x)} dx
⇒ 2I = \(\int_{0}^{a}\) f(x) {g(x) + g(a – x)}dx
⇒ 2I = \(\int_{0}^{a}\) f(x) × 4 dx
[∵ g(x) + g(a – x) = 4 given]
⇒ I = 2 \(\int_{0}^{a}\) f(x) dx.

Direction (20 – 21): Choose the correct answer.

Question 20.
The value of \(\int_{\frac{\pi}{2}}^{\frac{\pi}{2}}\) (x³ + x cos x + tan⁵ x + 1) dx is
(A) 0
(B) 2
(C) π
(D) 1
Solution.

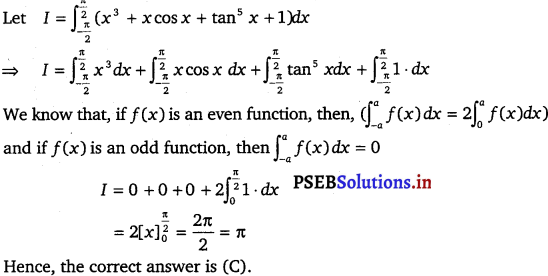
Question 21.
The value of \(\int_{0}^{\frac{\pi}{2}} \log \left(\frac{4+3 \sin x}{4+3 \cos x}\right)\) dx is
(A) 2
(B) \(\frac{3}{4}\)
(C) 0
(D) – 1
Solution.