PSEB 12th Class Maths Solutions Chapter 7 Integrals Ex 7.2

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 7 Integrals Ex 7.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 7 Integrals Ex 7.2

Direction (1 – 37): Integrate the following functions.

Question 1.
$\frac{2 x}{1+x^{2}}$
Solution.
∫ $\frac{2 x}{1+x^{2}}$ dx
Let 1 + x² = t
On differentiating w.rt. x, we get
2x dx = dt
⇒ x dx = $\frac{d t}{2}$
⇒ ∫ $\frac{2 x}{1+x^{2}}$ dx = ∫ $\frac{1}{t}$ dt
= log |t| + C
= log |1 + x²| + C

Question 2.
$\frac{(\log x)^{2}}{x}$
Sol.
∫ $\frac{(\log x)^{2}}{x}$ dx
Let log x = t
On differentiating w.r.t. x, we get
$\frac{1}{x}$ dx = dt
⇒ dx = x dt
⇒ ∫ $\frac{(\log x)^{2}}{x}$ dx = ∫ t² dt
= $\frac{t^{3}}{3}$ + C
= $\frac{(\log x)^{3}}{3}$ + C

Question 3.
$\frac{1}{x+x \log x}$
Solution.
∫ $\frac{1}{x+x \log x}$ dx = ∫ $\frac{1}{x(1+\log x)}$ dx
Let 1 + log x = t
On differentiating w.r.t. x, we get
$\frac{1}{x}$ dx = dt
⇒ dx = x dt
⇒ ∫ $\frac{1}{x+x \log x}$ dx = ∫ $\frac{1}{t}$ dt
= log |t| + C
= log |1 + log x| + C

Question 4.
sin x . sin (cos x)
Solution.
∫ sin x . sin(cos x) dx
Let cos x = t
On differentiating w.r.t. x, we get
– sin x dx = dt
⇒ ∫ sin x . sin (cos x) dx = – ∫ sin t dt
= – [- cos t] + C
= cos t + C = cos (cos x) + C

Question 5.
sin(ax + b) cos(ax + b)
Solution.
∫ sin(ax + b) cos(ax + b) dx
= – $\frac{1}{2}$ ∫ 2 sin (ax + b) cos(ax + b) dx
= – $\frac{1}{2}$ ∫ sin (2ax + 2b) dx
Let 2ax + 2b = t
On differentiating w.r.t. x, we get
2a dx = dt
∴ I = $\frac{1}{2}$ ∫ sin t . $\frac{d t}{2 a}$

= $\frac{1}{4 a}$ ∫ sin t dt

= – $\frac{1}{4 a}$ cos t + C

= – $\frac{1}{4 a}$ cos (2ax + 2) + C

Question 6.
$\sqrt{a x+b}$
Solution.
∫ $\sqrt{a x+b}$ dx
Let ax + b = t
On differentiating w.r.t. x, we get
a dx = dt
∴ dx = $\frac{1}{a}$ dt
⇒ ∫ $(a x+b)^{\frac{1}{2}} d x=\frac{1}{a} \int t^{\frac{1}{2}} d t$

= $\frac{1}{a}\left(\frac{t^{\frac{3}{2}}}{\frac{3}{2}}\right)$

= $\frac{2}{3 a}(a x+b)^{\frac{3}{2}}$ + C

Question 7.
x $\sqrt{x+2}$
Solution.
∫ x $\sqrt{x+2}$ dx
Let (x + 2) = t
On differentiating w.r.t. x, we get
dx = dt

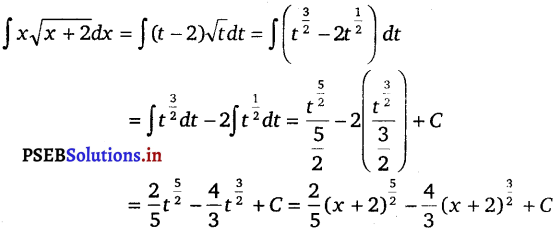
Question 8.
x $\sqrt{1+2 x^{2}}$
Solution.
∫ x $\sqrt{1+2 x^{2}}$ dx
Let 1 + 2x² = t
On differentiating w.r.t. x, we get
4x dx = dt
∫ x $\sqrt{1+2 x^{2}}$ dx = $\int \frac{\sqrt{t} d t}{4}=\frac{1}{4} \int t^{\frac{1}{2}} d t$

= $\frac{1}{4}\left(\frac{t^{\frac{3}{2}}}{\frac{3}{2}}\right)+C=\frac{1}{6}\left(1+2 x^{2}\right)^{\frac{3}{2}}+C$

Question 9.
(4x + 2) $\sqrt{x^{2}+x+1}$
Solution.
∫ (4x + 2) $\sqrt{x^{2}+x+1}$ dx
Let x² + 2x + 1 = t
On differentiating w.r.t. x, we get
(2x + 1) dx = dt
∫ (4x + 2) $\sqrt{x^{2}+x+1}$ dx = ∫ 2√t dt = 2 ∫ √t dt
= 2 $\left(\frac{t^{\frac{3}{2}}}{\frac{3}{2}}\right)$ + C

= $\frac{4}{3}\left(x^{2}+x+1\right)^{\frac{3}{2}}$ + C

Question 10.
$\frac{1}{x-\sqrt{x}}$
Solution.
∫ $\frac{1}{x-\sqrt{x}}$ dx = ∫ $\frac{1}{\sqrt{x}(\sqrt{x}-1)}$ dx
Let (√x – 1) = t
On differentiating w.r.t. x, we get
∴ $\frac{1}{2 \sqrt{x}}$ dx = dt
⇒ dx = 2√x dt
⇒ ∫ $\frac{1}{2 \sqrt{x}}$ dx = ∫ $\frac{1}{\sqrt{x} t} 2 \sqrt{x} d t=\int \frac{2}{t} d t$
= 2 log |t| + C
= 2 log |$\sqrt{x}-1$| + C

Question 11.
$\frac{x}{\sqrt{x+4}}$, x > 0
Solution.
∫ $\frac{x}{\sqrt{x+4}}$ dx
Let x + 4 = t
On differentiating w.r.t. x, we get
dx = dt

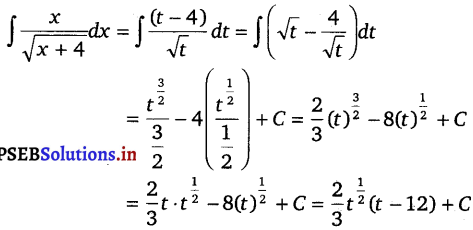
Question 11.
$\frac{x}{\sqrt{x+4}}$, x > 0
Solution.
∫ \(\frac{x}{\sqrt{x+4}}[latex] dx
Let x + 4 = t
On differentiating w.r.t. x, we get
dx = dt

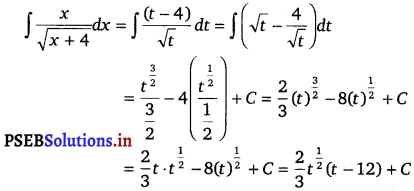
= [latex]\frac{2}{3}(x+4)^{\frac{1}{2}}\) (x + 4 – 12) + C

= $\frac{2}{3} \sqrt{x+4}$ (x – 8) + C

Question 12.
$\left(x^{3}-1\right)^{\frac{1}{3}} x^{5}$
Solution.
∫ $\left(x^{3}-1\right)^{\frac{1}{3}} x^{5}$ dx
Let x³ – 1 = t
On differentiating w.r.t. x, we get
3x² dx = dt
⇒ dx = $\frac{d t}{3 x^{2}}$
⇒ ∫ $\left(x^{3}-1\right)^{\frac{1}{3}} x^{5}$ dx = ∫ (x³ – 1)^{$\frac{4}{4}$} x³ x² dx

Question 13.
$\frac{x^{2}}{\left(2+3 x^{3}\right)^{3}}$
Solution.
∫ $\frac{x^{2}}{\left(2+3 x^{3}\right)^{3}}$ dx
On differentiating w.r.t. x, we get
9x² dx = dt
⇒ dx = $\frac{d t}{9 x^{2}}$
∫ $\frac{x^{2}}{\left(2+3 x^{3}\right)^{3}}$ dx = $\frac{1}{9} \int \frac{d t}{(t)^{3}}=\frac{1}{9}\left[\frac{t^{-3+1}}{-3+1}\right]+C$

= – $\frac{1}{18}\left(\frac{1}{t^{2}}\right)$ + C

= – $\frac{1}{18\left(2+3 x^{3}\right)^{2}}$ + C

Question 14.
$\frac{1}{x(\log x)^{m}}$, x > 0, m ≠ 1
Solution.
∫ $\frac{1}{x(\log x)^{m}}$ dx
Let log x = t
On differentiating w.r.t. x, we get
$\frac{1}{x}$ dx = dt
⇒ dx = x dt
∴ ∫ $\frac{1}{x(\log x)^{m}}$ dx = ∫ $\frac{d t}{(t)^{m}}$

= $\left(\frac{t^{-m+1}}{-m+1}\right)$ + C

= $\frac{(\log x)^{1-m}}{(1-m)}$ + C

Question 15.
$\frac{x}{9-4 x^{2}}$
Solution.
∫ $\frac{x}{9-4 x^{2}}$ dx
Let 9 – 4x² = t
On differentiating w.r.t. x, we get
– 8x dx = dt
⇒ dx = $\frac{d t}{-8 x}$
∫ $\frac{x}{9-4 x^{2}}$ dx = $\frac{-1}{8}$ ∫ $\frac{1}{t}$ dt
= $\frac{-1}{8}$ log |t| + C
= $\frac{-1}{8}$ log |9 – 4x²| + C

Question 16.
e^{2x +3}
Solution.
∫ e^{2x + 3} dx
Let 2x + 3 = t
On differentiating w.r.t. x, we get
2 dx = dt
⇒ dx = $\frac{1}{2}$ dt
∴ ∫ e^{2x + 3} dx = $\frac{1}{2}$ ∫ e^t dt
= $\frac{1}{2}$ (e^t) + C
= $\frac{1}{2}$ e^{(2x + 3)} + C

Question 18.
$\frac{e^{\tan ^{-1} x}}{1+x^{2}}$
Solution.
∫ $\frac{e^{\tan ^{-1} x}}{1+x^{2}}$ dx
Let tan^-1 x = t
⇒ $\frac{1}{1+x^{2}}$ dx = dt
⇒ dx = (1 + x²) dt
∴ ∫ $\frac{e^{\tan ^{-1} x}}{1+x^{2}}$ dx = ∫ e^t dt
= e^t + C
= e^tan-1 x + C

Question 19.
$\frac{e^{2 x}-1}{e^{2 x}+1}$
Solution.

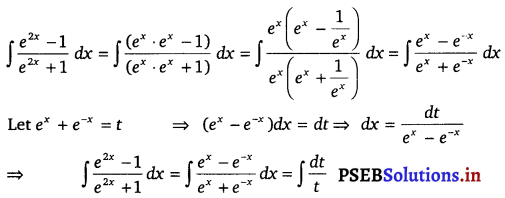
= log |t| + C
= log |e^x + e^-x| + C.

Question 20.
$\frac{e^{2 x}-e^{-2 x}}{e^{2 x}+e^{-2 x}}$
Solution.
∫ $\frac{e^{2 x}-e^{-2 x}}{e^{2 x}+e^{-2 x}}$ dx
Let e^2x + e^-2x = t
⇒ (2 e^2x – 2 e^-2x) dx = dt
⇒ dx = $\frac{d t}{2\left(e^{2 x}-e^{-2 x}\right)}$

∫ $\frac{e^{2 x}-e^{-2 x}}{e^{2 x}+e^{-2 x}}$ dx = ∫ $\frac{d t}{2 t}$

= $\frac{1}{2}$ ∫ $\frac{1}{t}$ dt

= $\frac{1}{2}$ log |t| + C

= $\frac{1}{2}$ log |e^2x + e^-2x| + C.

Question 21.
tan² (2x – 3)
Solution.
∫ tan² (2x – 3) dx = ∫ sec² (2x – 3) dx – ∫ 1 dx
Let 2x – 3 = t
⇒ 2 dx = dt
⇒ dx = $\frac{1}{2}$ dt
⇒ ∫ sec² (2x – 3) dx – ∫ 1 dx = $\frac{1}{2}$ ∫ (sec² t dt – ∫ 1 dx
= $\frac{1}{2}$ tan t – x + C
= $\frac{1}{2}$ tan (2x – 3) – x + C

Question 22.
sec² (7 – 4x)
Solution.
∫ sec² (7 – 4x) dx
Let 7 – 4x = t
⇒ – 4 dx = dt
⇒ dx = $\frac{d t}{-4}$

∴ ∫ sec² (7 – 4x) dx = $\frac{-1}{4}$ ∫ sec² t dt
= $\frac{-1}{4}$ (tan t) + C
= $\frac{-1}{4}$ tan (7 – 4x) + C

Question 23.
$\frac{\sin ^{-1} x}{\sqrt{1-x^{2}}}$
Solution.
∫ $\frac{\sin ^{-1} x}{\sqrt{1-x^{2}}}$ dx
Let sin^-1 x = t

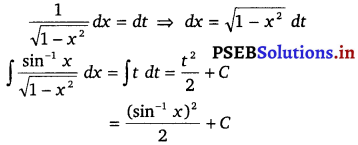
Question 24.
$\frac{2 \cos x-3 \sin x}{6 \cos x+4 \sin x}$
Solution.
∫ $\frac{2 \cos x-3 \sin x}{6 \cos x+4 \sin x}$ dx = ∫ $\frac{2 \cos x-3 \sin x}{2(3 \cos x+2 \sin x)}$ dx

Let 3 cos x + 2 sin x = t

⇒ (- 3 sin x + 2 cos x) dx = dt

⇒ dx = $\frac{d t}{2 \cos x-3 \sin x}$

∴ ∫ $\frac{2 \cos x-3 \sin x}{6 \cos x+4 \sin x}$ dx = ∫ $\frac{d t}{2 t}$ + $\frac{1}{2}$ ∫ $\frac{1}{t}$ dt

= $\frac{1}{2}$ log |t| + C

= $\frac{1}{2}$ log |2 sin x + 3 cos x| + C

Question 25.
$\frac{1}{\cos ^{2} x(1-\tan x)^{2}}$
Solution.
∫ $\frac{1}{\cos ^{2} x(1-\tan x)^{2}}$ dx = ∫ $\frac{\sec ^{2} x}{(1-\tan x)^{2}}$ dx
Let (1 – tan x) = t
⇒ – sec² x dx = dt
⇒ dx = $\frac{d t}{-\sec ^{2} x}$

∫ $\frac{\sec ^{2} x}{(1-\tan x)^{2}}$ dx = ∫ $\frac{-d t}{t^{2}}$
= – ∫ t² dt

= – $\left(\frac{-t^{-2+1}}{-2+1}\right)$ + C

= $\frac{1}{t}+C=\frac{1}{(1-\tan x)}$ + C

Question 26.
$\frac{\cos \sqrt{x}}{\sqrt{x}}$
Solution.
∫ $\frac{\cos \sqrt{x}}{\sqrt{x}}$ dx
Let √x = t
⇒ $\frac{1}{2 \sqrt{x}}$ dx = dt
⇒ dx = 2 √x dt
∫ $\frac{\cos \sqrt{x}}{\sqrt{x}}$ dx = 2 ∫ cos t dt
= 2 sin t + C
= 2 sin √x + C

Question 27.
$\sqrt{\sin 2 x}$ cos 2x
Solution.
∫ $\sqrt{\sin 2 x}$ cos 2x dx
Let sin 2x = t
⇒ 2 cos 2x dx = dt
⇒ dx = $\frac{d t}{2 \cos 2 x}$
∴ ∫ $\sqrt{\sin 2 x}$ cos 2x dx = $\frac{1}{2}$ ∫ (t)^{$\frac{1}{2}$} dt

= $\frac{1}{2}\left(\frac{t^{\frac{3}{2}}}{\frac{3}{2}}\right)$

= $\frac{1}{3} t^{\frac{3}{2}}$ + C

= $\frac{1}{3}(\sin 2 x)^{\frac{3}{2}}$ + C

Question 28.
$\frac{\cos x}{\sqrt{1+\sin x}}$
Solution.
∫ $\frac{\cos x}{\sqrt{1+\sin x}}$ dx
Let 1 + sin x = t
⇒ cos x dx = dt
⇒ dx = $\frac{d t}{\cos x}$

∫ $\frac{\cos x}{\sqrt{1+\sin x}}$ dx = $\frac{d t}{\sqrt{t}}$

= $\frac{t^{\frac{1}{2}}}{\frac{1}{2}}$ + C

= 2√t + C

= 2 ${\sqrt{1+\sin x}}$ + C

Question 29.
cot x log sin x
Solution.
∫ cot x log sin x dx
Let log sin x = t .
⇒ $\frac{1}{\sin x}$ . cos x dx = dt
⇒ cot x dx = dt
⇒ dx = $\frac{d t}{\cot x}$
∴ ∫ cot x log sin x dx = ∫ t dt
= $\frac{t^{2}}{2}$ + C
= $\frac{1}{2}$ (log sin x)² + C

Question 30.
$\frac{\sin x}{1+\cos x}$
Solution.
∫ $\frac{\sin x}{1+\cos x}$ dx
Let 1 + cos x = t
⇒ – sin x dx = dt
⇒ dx = $\frac{d t}{-\sin x}$
∴ ∫ $\frac{\sin x}{1+\cos x}$ dx = ∫ – $\frac{d t}{t}$
= – log |t| + C
= – log |1 + cos x| + C
= log $\frac{1}{|1+\cos x|}$ + C

Question 31.
$\frac{\sin x}{(1+\cos x)^{2}}$
Solution.
∫ $\frac{\sin x}{(1+\cos x)^{2}}$ dx
Let 1 + cos x = t
⇒ – sin x dx = dt
⇒ dx = $=\frac{d t}{-\sin x}$
∴ ∫ $\frac{\sin x}{(1+\cos x)^{2}}$ dx = ∫ – $\frac{d t}{t^{2}}$

= ∫ t^-2 dt

= $\frac{-t^{-2+1}}{-2+1}$ + C

= $\frac{1}{t}$ + C

= $\frac{1}{1+\cos x}$ + C

Question 32.
$\frac{1}{1+\cot x}$
Solution.

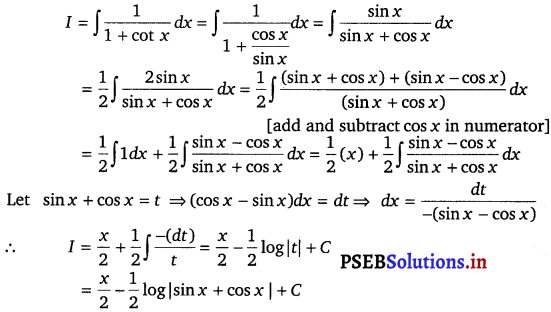
Question 33.
$\frac{1}{1-\tan x}$
Solution.

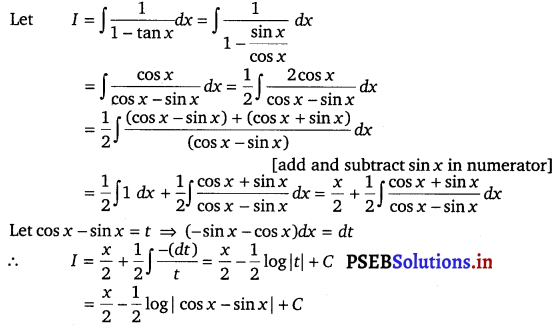
Question 34.
$\frac{\sqrt{\tan x}}{\sin x \cos x}$
Solution.
Let I = $\frac{\sqrt{\tan x}}{\sin x \cos x}$ dx

= ∫ $\frac{\sqrt{\tan x} \times \cos x}{\sin x \cos x \times \cos x}$ dx

= ∫ $\frac{\sqrt{\tan x}}{\tan x \cos ^{2} x}$ dx

= ∫ $\frac{\sec ^{2} x}{\sqrt{\tan x}}$ dx

Let x = tan t
⇒ sec² x dx = dt
⇒ dx = $\frac{d t}{\sec ^{2} x}$

∴ I = ∫ $\frac{d t}{\sqrt{t}}$

= ∫ t^{$-\frac{1}{2}$}

= 2√t + C

= 2√tan x + C

Question 35.
$\frac{(1+\log x)^{2}}{x}$
Solution.
∫ $\frac{(1+\log x)^{2}}{x}$ dx
Let 1 + log x = t
⇒ $\frac{1}{x}$dx = dt
⇒ dx = x dt
∴ ∫ $\frac{(1+\log x)^{2}}{x}$ dx = ∫ t² dt
= $\frac{t^{3}}{3}$ + C
= $\frac{(1+\log x)^{3}}{3}$ + C

Question 36.
$\frac{(x+1)(x+\log x)^{2}}{x}$
Solution.
∫ $\frac{(x+1)(x+\log x)^{2}}{x}$ dx = ∫ $\frac{x+1}{x}$ (x + log x)² dx

= ∫ (1 + $\frac{1}{x}$) (x + log x)² dx

Let x + log x = t
⇒ (1 + $\frac{1}{x}$) dx = dt

∴ ∫ (1 + $\frac{1}{x}$) (x + log x)² dx = ∫ t² dt

= $\frac{t^{3}}{3}$ + C

= $\frac{1}{3}$ (x + log x)³ + C

Question 37.
$\frac{x^{3} \sin \left(\tan ^{-1} x^{4}\right)}{1+x^{8}}$
Solution.
Let I = ∫ $\frac{x^{3} \sin \left(\tan ^{-1} x^{4}\right)}{1+x^{8}}$ dx

Let tan^-1 x⁴ = t
⇒ $\frac{1}{1+x^{8}}$ . 4x³ = $\frac{d t}{d x}=$

⇒ dx = $\frac{\left(1+x^{8}\right)}{4 x^{3}}$ dt

∴ I = ∫ $\frac{x^{3} \sin t}{\left(1+x^{8}\right)} \cdot \frac{1+x^{8} d t}{4 x^{3}}$

= $\frac{1}{4}$ ∫ sin t dt

= – $\frac{1}{4}$ cos t + C

Direction (38 – 39) : Choose the correct answer.

Question 38.
∫ $\frac{10 x^{9}+10^{x} \log _{e} 10}{x^{10}+10^{x}}$ dx equals
(A) 10^x – x¹⁰ + C

(B) 10^x + x¹⁰ + C

(C) (10^x – x¹⁰)^-1 + C

(D) log (10^x + x¹⁰) + C
Solution.
∫ $\frac{10 x^{9}+10^{x} \log _{e} 10}{x^{10}+10^{x}}$ dx
Let x¹⁰ + 10^x = t
⇒ dx = $\frac{d t}{10 x^{9}+10^{x} \log _{e} 10}$
∴ ∫ $\frac{10 x^{9}+10^{x} \log _{e} 10}{x^{10}+10^{x}}$ dx = ∫ $\frac{dt}{t}$
= log t + C
= log (10^x + x¹⁰) + C
Hence, the correct answer is (D).

Question 39.
∫ $\frac{d x}{\sin ^{2} x \cos ^{2} x}$ ,
(A) tan x + cot x + C
(B) tan x – cot x + C
(C) tan x cot x + C
(D) tan x – cot 2x + C
Solution.

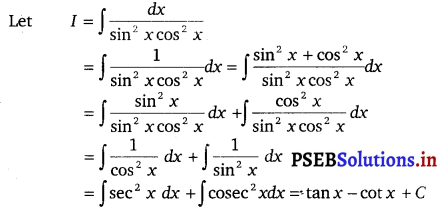
Hence, the correct answer is (B).