PSEB 12th Class Maths Solutions Chapter 7 Integrals Ex 7.4

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 7 Integrals Ex 7.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 7 Integrals Ex 7.4

Question 1.
$\frac{3 x^{2}}{x^{6}+1}$
Solution.
∫ $\frac{3 x^{2}}{x^{6}+1}$ dx = ∫ $\frac{3 x^{2}}{\left(x^{3}\right)^{2}+1}$ dx
Let x³ = t
⇒ 3x² dx = dt
⇒ dx = $\frac{d t}{3 x^{2}}$
∫ $\frac{3 x^{2}}{\left(x^{3}\right)^{2}+1}$ dx = ∫ $\frac{d t}{t^{2}+1}$
= tan^-1 t + C
= tan^-1 (x³) + C

Question 2.
$\frac{1}{\sqrt{1+4 x^{2}}}$
Solution.
∫ $\frac{1}{\sqrt{1+4 x^{2}}}$ dx = ∫ dx
Let 2x = t
⇒ 2 dx = dt
⇒ dx = $\frac{1}{2}$
∴ $\int \frac{1}{\sqrt{1+4 x^{2}}} d x=\frac{1}{2} \int \frac{d t}{\sqrt{1+t^{2}}}$

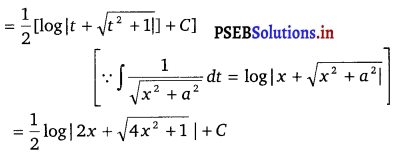
Question 3.
$\frac{1}{\sqrt{(2-x)^{2}+1}}$
Solution.

Question 4.
$\frac{1}{\sqrt{9-25 x^{2}}}$
Solution.

Question 5.
$\frac{3 x}{1+2 x^{4}}$
Solution.
∫ $\frac{3 x}{1+2 x^{4}}$ dx = $\frac{3}{2} \int \frac{x d x}{\frac{1}{2}+x^{4}}=\frac{3}{2} \int \frac{x d x}{\frac{1}{2}+\left(x^{2}\right)^{2}}$

Let x² = t
⇒ 2x = $\frac{d t}{d x}$

⇒ dx = $\frac{d t}{2 x}$

Question 6.
$\frac{x^{2}}{1-x^{6}}$
Solution.

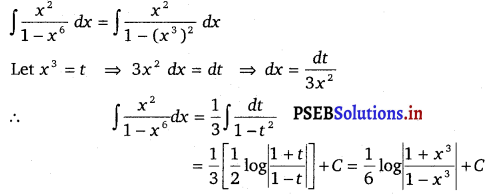
Question 7.
$\frac{x-1}{\sqrt{x^{2}-1}}$
Solution.

Question 8.
$\frac{x^{2}}{\sqrt{x^{6}+a^{6}}}$
Solution.

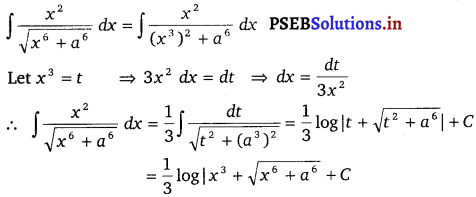
Question 9.
$\frac{\sec ^{2} x}{\sqrt{\tan ^{2} x+4}}$
Solution.

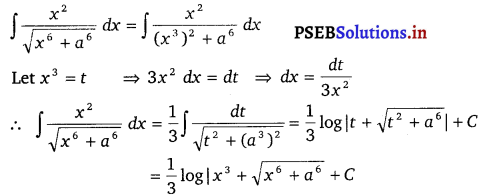
Question 10.
$\frac{1}{\sqrt{x^{2}+2 x+2}}$
Solution.

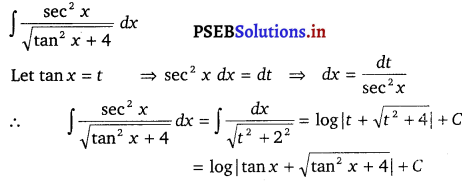
Question 11.
$\frac{1}{9 x^{2}+6 x+5}$
Solution.

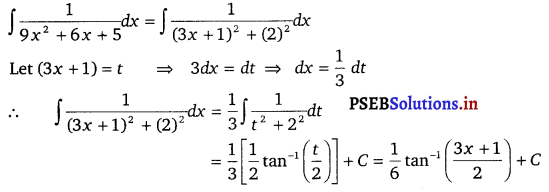
Question 12.
$\frac{1}{\sqrt{7-6 x-x^{2}}}$
Solution.
7 – 6x – x² can be written as 7 – (x² + 6x + 9 – 9).
Therefore, 7 – (x² + 6x + 9 – 9) = 16 – (x² + 6x + 9)
= 16 – (x + 3)²
= (4)² – (x + 3)²

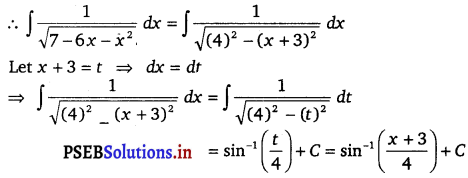
Question 13.
$\frac{1}{\sqrt{(x-1)(x-2)}}$
Solution.
(x – 1) (x – 2) can be written as x² – 3x + 2

Question 14.
$\frac{1}{\sqrt{8+3 x-x^{2}}}$
Solution.
8 + 3x – x² can be written as – (x² – 3x + $\frac{9}{4}$ – $\frac{9}{4}$)

Therefore, 8 – (x² – 3x + $\frac{9}{4}$ – $\frac{9}{4}$) = $\frac{41}{4}-\left(x-\frac{3}{2}\right)^{2}$

Question 15.
$\frac{1}{\sqrt{(x-a)(x-b)}}$
Solution.
(x – a) (x – b) can be written as x² – (a + b) x + ab
Therefore,

Question 16.
$\frac{4 x+1}{\sqrt{2 x^{2}+x-3}}$
Solution.
∫ $\frac{4 x+1}{\sqrt{2 x^{2}+x-3}}$ dx
Let 2x² + x – 3 = t
⇒ (4x + 1) dx = dt
⇒ dx = $\frac{d t}{4 x+1}$

= $\int \frac{d t}{\sqrt{t}}=\int t^{-\frac{1}{2}} d t=\frac{t^{-\frac{1}{2}+1}}{\frac{1}{2}}+C=2 \sqrt{t}+C$

= 2 $\sqrt{2 x^{2}+x-3}$ + C

Question 17.
$\frac{x+2}{\sqrt{x^{2}-1}}$

Solution.

Question 18.
$\frac{5 x-2}{1+2 x+3 x^{2}}$
Solution.
Let 5x – 2 = A $\frac{d}{d x}$ (1 +2x + 3x²) + B
⇒ 5x – 2 = A (2 + 6x) + B
Equating the coefficient of x and constant term on both sides, we get
5 = 6A
⇒ A = $\frac{5}{6}$ ;
2A + B = – 2
⇒ B = – $\frac{11}{3}$

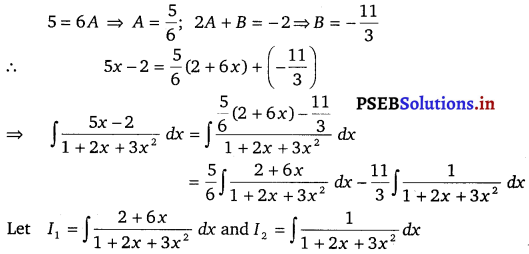
Question 19.
$\frac{6 x+7}{\sqrt{(x-5)(x-4)}}$
Solution.
$\frac{6 x+7}{\sqrt{(x-5)(x-4)}}=\frac{6 x+7}{\sqrt{x^{2}-9 x+20}}$

Let 6x + 7 = A $\frac{d}{d x}$ (x² – 9x + 20) + B
⇒ 6x + 7 = A (2x – 9) + B
Equating the coefficients of x and constant term, we get
2A = 6
⇒ A = 3;
– 9A + B = 7
⇒ B = 34
∴ 6x + 7 = 3 (2x – 9) + 34

Question 20.
$\frac{x+2}{\sqrt{4 x-x^{2}}}$
Solution.
∫ $\frac{x+2}{\sqrt{4 x-x^{2}}}$ dx

Question 21.
$\frac{x+2}{\sqrt{x^{2}+2 x+3}}$
Solution.

Substituting equations (ii) and (iii) in equation (i), we get
∫ $\frac{x+2}{\sqrt{x^{2}+2 x+3}}$ dx = $\frac{1}{2}\left[2 \sqrt{x^{2}+2 x+3}\right]+\log \mid(x+1)+\sqrt{x^{2}+2 x+3 \mid}$

= $\sqrt{x^{2}+2 x+3}+\log \mid(x+1)+\sqrt{x^{2}+2 x+3 \mid}$ + C

Question 22.
$\frac{x+3}{x^{2}-2 x-5}$
Solution.
Let (x + 3) = A $\frac{d}{d x}$ (x² – 2x – 5) + B
⇒ (x + 3) = A (2x – 2) + B
⇒ x + 3 = 2Ax – 2A + B
On equating the coefficients of x and constant term on both sides, we get
2A = 1
⇒ A = $\frac{1}{2}$;
– 2A + B = 3
⇒ B = 4
⇒ (x + 3) = $\frac{1}{2}$ (2x – 2) + 4

Question 23.
$\frac{5 x+3}{\sqrt{x^{2}+4 x+10}}$
Solution.
Let 5x + 3 = A $\frac{d}{d x}$ (x² + 4x + 10) + B
⇒ 5x + 3 = A (2x + 4) + B
⇒ 5x + 3 = 2Ax + 4A + B
On equating the coefficients of x and constant term, we get
2A = 5
A = $\frac{5}{2}$;
4A + B = 3
⇒ B = – 7
⇒ 5x + 3 = (2x + 4) – 7

Direction (24 – 25): Choose the correct answer:

Question 24.
∫ $\int \frac{d x}{x^{2}+2 x+2}$ equals
(A) x tan^-1 (x + 1) + C
(B) tan^-1 (x + 1) + C
(C) (x + 1) tan^-1 x + C
(D) tan^-1 x + C
Solution.
∫ $\int \frac{d x}{x^{2}+2 x+2}$ dx = $\int \frac{d x}{\left(x^{2}+2 x+1\right)+1}=\int \frac{1}{(x+1)^{2}+(1)^{2}} d x$
Let x + 1 = t
⇒ dx = dt
∴ ∫ $\frac{1}{t^{2}+1^{2}}$ dt = $\frac{1}{1} \tan ^{-1}\left(\frac{t}{1}\right)$ + C

= tan $\left(\frac{x+1}{1}\right)$ + C

= tan^-1 (x + 1) + C
Hence, the correct answer is (B).

Question 25.
∫ $\frac{d x}{\sqrt{9 x-4 x^{2}}}$ equals
(A) $\frac{1}{9} \sin ^{-1}\left(\frac{9 x-8}{8}\right)$ + C

(B) $\frac{1}{2} \sin ^{-1}\left(\frac{8 x-9}{9}\right)$

(C) $\frac{1}{3} \sin ^{-1}\left(\frac{9 x-8}{8}\right)$

(D) $\frac{1}{2} \sin ^{-1}\left(\frac{9 x-8}{9}\right)$
Solution.

Hence, the correct answer is (B).