PSEB 12th Class Maths Solutions Chapter 7 Integrals Ex 7.6

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 7 Integrals Ex 7.6 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 7 Integrals Ex 7.6

Direction (1 – 22): Integrate the functions:

Question 1.
x sin x
Solution.
Let I = ∫ x sin x dx
Taking x as first function and sin x as second function and integrating by parts, we get
I = x ∫ sin x dx – ∫ {(\(\frac{d}{d x}\) (x)) ∫ sin x dx} dx
= x (- cos x) – ∫ 1 . (- cos x) dx
= – x cos x + sin x + C

Question 2.
x sin 3x
Solution.
Let I = ∫ x sin 3x dx
Taking x as first function and sin3x as second function and integrating by parts, we get

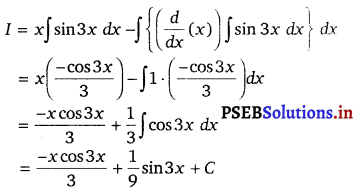
Question 3.
x² e^x
Solution.
Let I = ∫ x² e^x dx
Taking x² as first function and e^x as second function and integrating by parts,we get
I = x² ∫ e^x dx – ∫ {(\(\frac{d}{d x}\) x²) ∫ e^x dx} dx
= x² e^x – ∫ 2x . e^x dx
= x² e^x – 2 ∫ x . e^x dx
Again integrating by parts, we get
= x² e^x – 2 [x . ∫ e^x dx – ∫ {(\(\frac{d}{d x}\) x) ∫ e^x dx} dx]
= x² e^x – 2 [x e^x – e^x dx]
= x² e^x – 2 [x e^x – e^x]
= x² e^x – 2x e^x + 2 e^x + C
= e^x (x² – 2x + 2) + C

Question 4.
x log x
Solution.
Let I = ∫ x log x dx
Taking log x as first function and x as second function and integrating by parts, we get

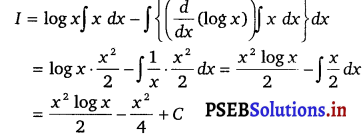
Question 5.
x log 2x
Solution.
Let I = ∫ x log 2x dx
Taking log 2x as first function and x as second function and integrating by parts, we get

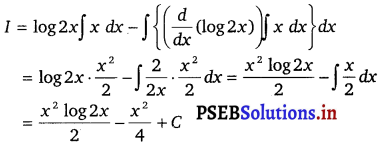
Question 6.
x² log x
Solution.
Let I = ∫ x² log x dx
Taking log x as first function and x² as second function and integrating by parts, we get

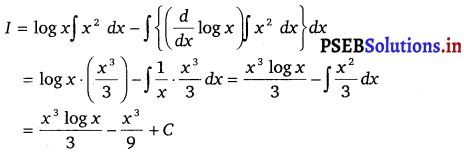
Question 7.
x sin^-1 x
Solution.
Let I = ∫ x sin^-1 x dx
Taking sin^-1 x as first function and x as second function and integrating by parts, we get

Question 8.
x tan^-1 x
Solution.
Let I = ∫ x tan^-1 x dx
Taking tan^-1 x as first function and x as second function and integrating by parts, we get

Question 9.
x cos^-1 x
Solution.
Let I = ∫ x cos^-1 x dx
Taking cos^-1 x as first function and x as second function and integrating by parts, we get

Question 10.
(sin ^-1 x)²
Solution.
Let I = ∫ (sin ^-1 x)² dx
Taking (sin ^-1 x)² as first function and x as second function and integrating by parts, we get

Question 11.
\(\frac{x \cos ^{-1} x}{\sqrt{1-x^{2}}}\)
Solution.
Let I = ∫ \(\frac{x \cos ^{-1} x}{\sqrt{1-x^{2}}}\) dx

= \(\frac{-1}{2} \int \frac{-2 x}{\sqrt{1-x^{2}}} \cdot \cos ^{-1} x\) dx

Taking cos x as first function and \(\left(\frac{-2 x}{\sqrt{1-x^{2}}}\right)\) as second function and integrating by parts, we get

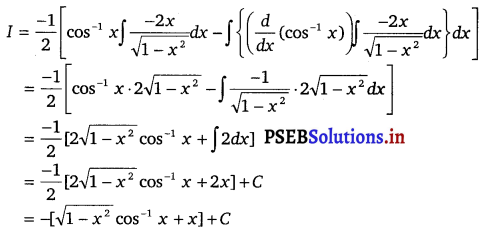
Question 12.
x sec² x
Solution.
Let I = ∫ x sec² x dx
Taking x as first function and sec² x as second function and integrating by parts, we get
I = x ∫ sec² x dx – ∫ [(\(\frac{d}{d x}\) (x)) ∫ sec² x dx] dx
= x tan x – ∫ 1 . tan x dx
= x tan x + log |cos x| + C

Question 13.
tan^-1 x
Solution.
Let I = ∫ 1 . tan^-1 x dx
Taking tan^-1 x as first function and 1 as second function and integrating by parts, we get

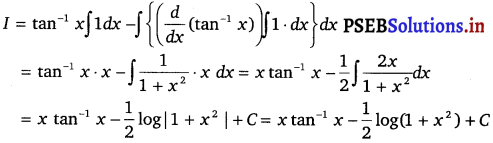
Question 14.
x (log x)²
Solution.
Let I = ∫ x (log x)² dx
Taking (log x)² as first function and x as second function and integrating by parts, we get

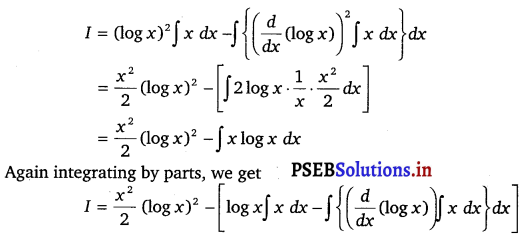
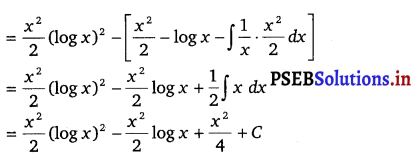
Question 15.
(x² + 1) log x
Solution.
Let I = ∫ (x² + 1) log x dx
= ∫ (log x) . (x² + 1) dx
Taking (log x) as first function and (x² + 1) as second function and integrating by parts, we get

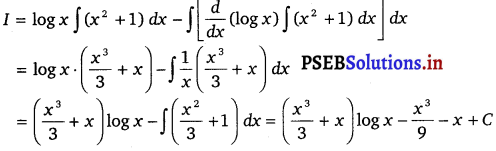
Question 16.
e^x (sin x + cos x)
Solution.
Let I = ∫ e^x (sin x + cos x) dx
Let f(x) = sin x
⇒ f’(x) = cos x
∴ I = ∫ ex {f(x) + f'(x)}dx
We know that, ∫ex {f(x) + f’(x)}dx = e^x f(x) + C
∴ I = e^x sin x + C

Question 17.
\(\frac{x e^{x}}{(1+x)^{2}}\)
Solution.

Question 18.
e^x \(\left(\frac{1+\sin x}{1+\cos x}\right)\)
Solution.

Question 19.
e^x \(\left(\frac{1}{x}-\frac{1}{x^{2}}\right)\)
Solution.
Let I = ∫ e^x \(\left(\frac{1}{x}-\frac{1}{x^{2}}\right)\) dx
Put \(\frac{e^{x}}{x}\) = t; i.e., \(\frac{1}{x}\) = t, so that,

\(\left[e^{x} \cdot\left(-\frac{1}{x^{2}}\right)+\frac{1}{x} \cdot e^{x}\right]\) dx = dt

I = ∫ dt = t + C = \(\frac{e^{x}}{x}\) + C

Question 20.
\(\frac{(x-3) e^{x}}{(x-1)^{3}}\)
Solution.

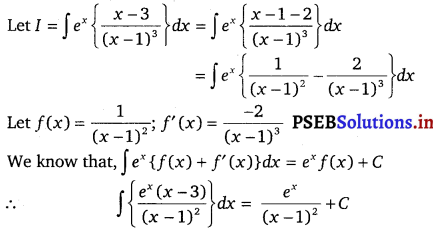
Question 21.
e^2x sin x
Solution.
Let I = ∫ e^2x sin x dx …………….(i)
Integrating by parts, we get

Question 22.
sin^-1 \(\left(\frac{2 x}{1+x^{2}}\right)\)
Solution.
Let x = tan θ so that dx = sec² θ dθ
∴ sin^-1 \(\left(\frac{2 x}{1+x^{2}}\right)\) = sin^-1 \(\left(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right)\)
= sin^-1 (sin 2θ) = 2θ

∴ ∫ sin^-1 \(\left(\frac{2 x}{1+x^{2}}\right)\) dx = ∫ 2θ . secsup>2 θ dθ
= 2 ∫ θ . sec² θ dθ
Integrating by parts, we get
\(2\left[\theta \cdot \int \sec ^{2} \theta d \theta-\int\left\{\left(\frac{d}{d \theta} \theta\right) \int \sec ^{2} \theta d \theta\right\} d \theta\right]\) = 2 [θ . tan θ – ∫ tan θ dθ]

= 2 [θ tan θ + log |cos θ|] + C

= 2 [x tan^-1 x + log \(\left|\frac{1}{\sqrt{1+x^{2}}}\right|\)] + C
= 2x tan^-1 x + 2 log (1 + x²)^{–\(\frac{1}{2}\)} + C
= 2x tan^-1 x + 2 [- \(\frac{1}{2}\) log (1 + x²)] + C
= 2x tan^-1 x – log (1 + x²) + C

Direction (23 – 24): Choose the correct answer in the given question.

Question 23.
∫ x² e^x3 dx equals
(A) \(\frac{1}{3}\) e^x3 + C
(B) \(\frac{1}{3}\) e^x2 + C
(C) \(\frac{1}{2}\) e^x3 + C
(D) \(\frac{1}{2}\) e^x2 + C
Sol.
Let I = ∫ x² e^x3 dx
Also, let x³ = t
⇒ 3x² dx = dt
⇒ I = \(\frac{1}{3}\) ∫ e^t dt
= \(\frac{1}{3}\) (e^t) + C
= \(\frac{1}{3}\) e^x3 + C
Hence, the correct answer is (A).

Question 24.
∫ e^x sec x (1 + tan x) dx equals
(A) e^x cos x + C
(B) e^x sec x + C
(C) e^x sin x + C
(D) e^x tan x + C
Sol.
∫ e^x secx(1 + tan x) dx
Let I = ∫ e^x sec x (1 + tan x) dx
= ∫ e^x (sec x + sec x tan x) dx
Also, let sec x = f(x). sec x tan x = f’(x)
We know that, ∫ e^x {f(x) + f’(x)}dr = e^x f(x) + C
∴ I = e^x sec x + C
Hence, the correct answer is (B). Textbook Exercise Questions and Answers.