PSEB 12th Class Maths Solutions Chapter 7 Integrals Miscellaneous Exercise

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 7 Integrals Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 7 Integrals Miscellaneous Exercise

Question 1.
\(\frac{1}{x-x^{3}}\)
Solution.
\(\frac{1}{x-x^{3}}=\frac{1}{x\left(1-x^{2}\right)}=\frac{1}{x(1-x)(1+x)}\)

Let \(\frac{1}{x(1-x)(1+x)}=\frac{A}{x}+\frac{B}{(1-x)}+\frac{C}{1+x}\) ………………..(i)

Equating the coefficients of x², x, and constant term, we get
– A + B – C = 0
B + C = 0, A = 1
On solving these equations, we get
A = 1, B = \(\frac{1}{2}\) and C = – \(\frac{1}{2}\)
From equation (i), we get

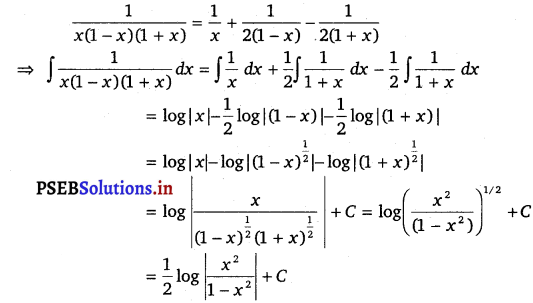
Question 2.
\(\frac{1}{\sqrt{x+a}+\sqrt{(x+b)}}\)
Solution.

= \(\frac{1}{(a-b)}\left[\frac{(x+a)^{\frac{3}{2}}}{\frac{3}{2}}-\frac{(x+b)^{\frac{3}{2}}}{\frac{3}{2}}\right]\)

= \(\frac{2}{3(a-b)}\left[(x+a)^{\frac{3}{2}}-(x+b)^{\frac{3}{2}}\right]\) + C

Question 3.
\(\frac{1}{x \sqrt{a x-x^{2}}}\) [Hint: Put x = \(\frac{a}{t}\)]
Solution.

Question 4.
\(\frac{1}{x^{2}\left(x^{4}+1\right)^{\frac{3}{4}}}\)
Solution.

Question 5.
Evaluate: \(\frac{1}{x^{\frac{1}{2}}+x^{\frac{1}{3}}}\) [Hint: \(\), put x = t⁶]
Solution.

Question 6.
\(\frac{5 x}{(x+1)\left(x^{2}+9\right)}\)
Solution.
Let \(\frac{5 x}{(x+1)\left(x^{2}+9\right)}=\frac{A}{(x+1)}+\frac{B x+C}{\left(x^{2}+9\right)}\) ………..(i)
⇒ 5x = A(x² + 9) + (Bx + C) (x + 1)
⇒ 5x = Ax² + 9A + Bx² +Bx + Cx + C
Equating the coefficients of x², x, and constant term, we get
A + B = 0;
B + C = 5;
9A + C = 0
On solving these equations, we get
A = – \(\frac{1}{2}\); B = \(\frac{1}{2}\) and C = \(\frac{9}{2}\)
From equation (i), we get

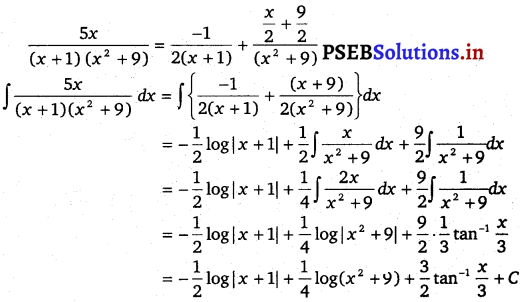
Question 7.
\(\frac{\sin x}{\sin (x-a)}\)
Solution.
\(\frac{\sin x}{\sin (x-a)}\)
Let x – a = t
⇒ dx = dt
∫ \(\frac{\sin x}{\sin (x-a)}\) dx = ∫ \(\frac{\sin (t+a)}{\sin t}\) dt

= ∫ \(\frac{\sin t \cos a+\cos t \sin a}{\sin t}\) dt

= ∫ (cos a + cos t sin a) dt
= t cos a + sin a log |sin t| + C₁
= (x – a) cos a + sin a log sin (x – a) + C₁
= x cos a + sin a log sin (x – a) – a cos a + C₁
= sin a log sin (x – a) + x cos a + C

Question 8.
\(\frac{e^{5 \log x}-e^{4 \log x}}{e^{3 \log x}-e^{2 \log x}}\)
Solution.

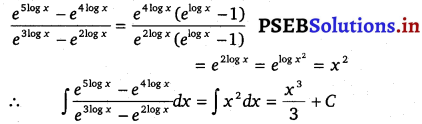
Question 9.
\(\frac{\cos x}{\sqrt{4-\sin ^{2} x}}\)
Solution.

Question 10.
\(\frac{\sin ^{8} x-\cos ^{8} x}{1-2 \sin ^{2} x \cos ^{2} x}\)
Solution.

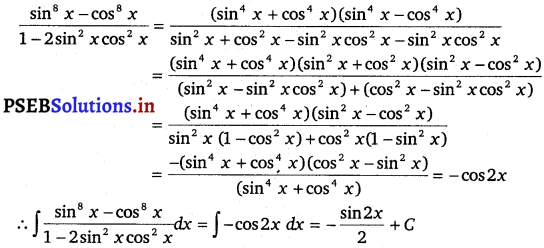
Question 11.
\(\frac{1}{\cos (x+a) \cos (x+b)}\)
Solution.

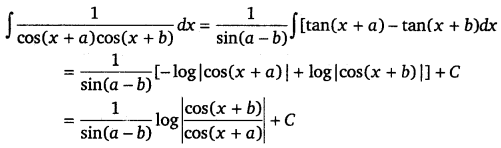
Question 12.
\(\frac{x^{3}}{1-x^{8}}\)
Solution.
\(\frac{x^{3}}{1-x^{8}}\)
Let x⁴ = t
⇒ 4x³ dx = dt
⇒ \(\int \frac{x^{3}}{\sqrt{1-x^{8}}} d x=\frac{1}{4} \int \frac{d t}{\sqrt{1-t^{2}}}\)

= \(\frac{1}{4}\) sin^-1 t + C

= \(\frac{1}{4}\) sin^-1 (x⁴) + C
[∵ ∫ \(\frac{d x}{\sqrt{a^{2}-x^{2}}}=\sin ^{-1}\left(\frac{x}{a}\right)\)]

Question 13.
\(\frac{e^{x}}{\left(1+e^{x}\right)\left(2+e^{x}\right)}\)
Solution.

Question 14.
\(\frac{1}{\left(x^{2}+1\right)\left(x^{2}+4\right)}\)
Solution.
\(\frac{1}{\left(x^{2}+1\right)\left(x^{2}+4\right)}=\frac{A x+B}{\left(x^{2}+1\right)}+\frac{C x+D}{\left(x^{2}+4\right)}\) …………..(i)

⇒ 1 = (Ax + B) (x² + 4) + (Cx + D) (x² + 1)
⇒ 1 = Ax³ + 4Ax + Bx² + 4B + Cx³ + Cx + Dx² + D
Equating the coefficients of x³, x², x, and constant term, we get
A + C = 0;
B + D = 0;
4A + C = 0;
4B + D = 1
On solving these equations, we get
A = 0, B = 1, C = 0 and D = – \(\frac{1}{3}\)

From equation (i), we get

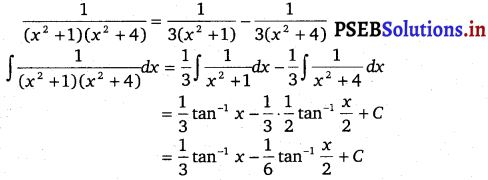
Question 15.
cos³ x e^{log sin x}
Solution.
cos³ x e^{log sin x} = cos³ × x sin x
Let cos x = t
⇒ – sin x dx = dt
⇒ ∫ cos³ x e^{log sin x} dx = ∫ cos³ x sin x dx
= – ∫ t³ dt
= \(\frac{t^{4}}{4}\) + C

= – \(\frac{\cos ^{4} x}{4}\) + C

Question 16.
e^{3 log x} (x⁴ + 1)^-1
Solution.

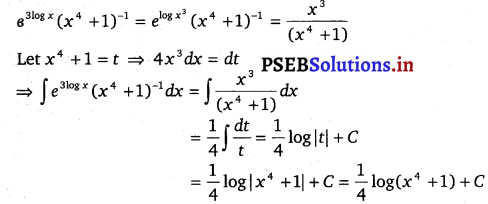
Question 17.
f'(ax + b) [f(ax + b)]ⁿ
Solution.
f'(ax + b) [f(ax + b)]ⁿ
Let f (ax + b) = t
⇒ af’(ax + b) dx = dt
⇒ f’(ax + b)[f(ax + b)]ⁿ dx = \(\frac{1}{a}\) ∫ tⁿ dt

= \(\frac{1}{a}\left[\frac{t^{n+1}}{n+1}\right]\)

= \(\frac{1}{a(n+1)}\) f(ax + b)ⁿ⁺¹ + C

Question 18.
\(\frac{1}{\sqrt{\sin ^{3} x \sin (x+\alpha)}}\)
Solution.
\(\frac{1}{\sqrt{\sin ^{3} x \sin (x+\alpha)}}=\frac{1}{\sqrt{\sin ^{3} x(\sin x \cos \alpha+\cos x \sin \alpha)}}\)

= \(\frac{1}{\sqrt{\sin ^{4} x \cos \alpha+\sin ^{3} x \cos x \sin \alpha}}\)

Question 19.
\(\frac{\sin ^{-1} \sqrt{x}-\cos ^{-1} \sqrt{x}}{\sin ^{-1} \sqrt{x}+\cos ^{-1} \sqrt{x}}\), x ∈ [0, 1]
Solution.

Question 20.
\(\sqrt{\frac{1-\sqrt{x}}{1+\sqrt{x}}}\)
Solution.

Question 21.
\(\frac{2+\sin 2 x}{1+\cos 2 x}\) e^x
Solution.
Let I = ∫ (\(\frac{2+\sin 2 x}{1+\cos 2 x}\)) e^x dx

= ∫ \(\left(\frac{2+2 \sin x \cos x}{2 \cos ^{2} x}\right)\) e^x dx

= ∫ \(\left(\frac{1+\sin x \cos x}{\cos ^{2} x}\right)\) e^x dx

= ∫ (sec² x + tan x) e^x dx
Let f(x) = tan x
⇒ f’(x) = sec² x
I = ∫ [f(x) + f'(x)] e^x dx
= e^x f(x) + C
= e^x tan x + C

Question 22.
\(\frac{x^{2}+x+1}{(x+1)^{2}(x+2)}\)
Solution.
\(\frac{x^{2}+x+1}{(x+1)^{2}(x+2)}=\frac{A}{(x+1)}+\frac{B}{(x+1)^{2}}+\frac{C}{(x+2)}\) …………..(i)

⇒ x² + x + 1 = A (x + 1) (x + 2) + B (x + 2) + C(x² +2x+1)
⇒ x² + x + 1 = A(x² + 3x + 2) + B (x + 2) + C(x² + 2x + 1)
⇒ x² + x + 1 = (A + C) x² + (3A +B + 2C) x + (2A + 2B + C)
Equating the coefficients of x2, x, and constant term, we get
A + C = 1;
3A + B + 2C = 1;
2A + 2B + C = 1
On solving these equations, we get
A = – 2, B = 1 andC = 3
From equation (i), we get

\(\frac{x^{2}+x+1}{(x+1)^{2}(x+2)}=\frac{-2}{(x+1)}+\frac{3}{(x+2)}+\frac{1}{(x+1)^{2}}\)

∫ \(\frac{x^{2}+x+1}{(x+1)^{2}(x+2)}\) dx = \(-2 \int \frac{1}{x+1} d x+3 \int \frac{1}{(x+2)} d x+\int \frac{1}{(x+1)^{2}} d x\)

= – 2 log |x + 1| + 3 log |x + 2| – \(\frac{1}{(x+1)}\) + C.

Question 23.
tan^-1 \(\sqrt{\frac{1-x}{1+x}}\)
Solution.
Let I = ∫ tan^-1 \(\sqrt{\frac{1-x}{1+x}}\) dx
Let x = cos θ
⇒ dx = – sin θ dθ
I = ∫ tan^-1 \(\sqrt{\frac{1-\cos \theta}{1+\cos \theta}}\) (- sin θ dθ)

= – ∫ tan^-1 \(\sqrt{\frac{2 \sin ^{2} \frac{\theta}{2}}{2 \cos ^{2} \frac{\theta}{2}}}\) sin θ dθ

= – ∫ tan^-1 tan \(\frac{\theta}{2}\) . sin θ dθ

= – \(\frac{1}{2}\) ∫ θ . sin θ dθ

= – \(\frac{1}{2}\) [θ – cos θ] – ∫ 1 . (- cos θ) dθ

= – \(\frac{1}{2}\) [- θ cos θ + sin θ]

= + \(\frac{1}{2}\) θ cos θ – \(\frac{1}{2}\) sin θ

= \(\frac{1}{2}\) cos^-1 x . x – \(\frac{1}{2}\) \(\sqrt{1-x^{2}}\) + C

= \(\frac{x}{2}\) cos^-1 x – \(\frac{1}{2}\) \(\sqrt{1-x^{2}}\) + C

= \(\frac{1}{2}\) [x cos^-1 x – \(\sqrt{1-x^{2}}\)) + C

Question 24.
\(\frac{\sqrt{x^{2}+1\left[\log \left(x^{2}+1\right)-2 \log x\right]}}{x^{4}}\)
Solution.

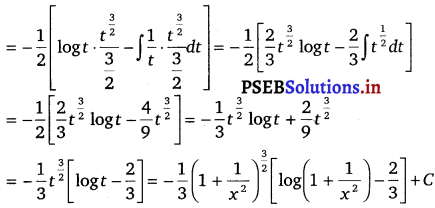
Direction (25 – 33): Evaluate the definite integral.

Question 25.
\(\cdot \int_{\frac{\pi}{2}}^{\pi} e^{x}\left(\frac{1-\sin x}{1-\cos x}\right)\) dx
Solution.

Question 26.
\(\int_{0}^{\frac{\pi}{4}} \frac{\sin x \cos x}{\cos ^{4} x+\sin ^{4} x}\) dx
Solution.
Let I = \(\int_{0}^{\frac{\pi}{4}} \frac{\sin x \cos x}{\cos ^{4} x+\sin ^{4} x}\) dx

= ∫ \(\int_{0}^{\frac{\pi}{4}} \frac{\cos ^{4} x}{\frac{\cos ^{4} x+\sin ^{4} x}{\cos ^{4} x}}\) dx

= ∫ \(\int_{0}^{\frac{\pi}{4}} \frac{\tan x \sec ^{2} x}{1+\tan ^{4} x}\) dx

Let tan² x = t
⇒ 2 tan x sec² x dx = dt
When x = 0, t = 0 and when x = \(\frac{\pi}{4}\), t = 1
∴ I = \(\frac{1}{2}\left[\tan ^{-1} t\right]_{0}^{1}\)

= \(\frac{1}{2}\) [tan^-1 1 – tan^-21 0]

= \(\frac{1}{2}\left[\frac{\pi}{4}\right]=\frac{\pi}{8}\)

Question 27.
\(\int_{0}^{\frac{\pi}{2}} \frac{\cos ^{2} x d x}{\cos ^{2} x+4 \sin ^{2} x}\) dx
Solution.

Let 2 tan x = t
⇒ 2 sec² x dx = dt
When x = 0, t = 0 and when x = \(\frac{\pi}{2}\), t = ∞
⇒ I = \(\int_{0}^{\frac{\pi}{2}} \frac{2 \sec ^{2} x}{1+4 \tan ^{2} x} d x=\int_{0}^{\infty} \frac{d t}{1+t^{2}}\)

= \(\left[\tan ^{-1} t\right]_{0}^{\infty}\)

= [tan (∞) – tan (o)] = \(\frac{\pi}{2}\)
Therefore, from Eq. Ci), we get
I = \(-\frac{\pi}{6}+\frac{2}{3}\left[\frac{\pi}{2}\right]=\frac{\pi}{3}-\frac{\pi}{6}=\frac{\pi}{6}\)

Question 28.
\(\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{\sin x+\cos x}{\sqrt{\sin 2 x}}\)
Solution.
Let I = \(\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{\sin x+\cos x}{\sqrt{\sin 2 x}}\) dx

= \(\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{(\sin x+\cos x)}{\sqrt{-(-\sin 2 x)}}\) dx

Question 29.
\(\int_{0}^{1} \frac{d x}{\sqrt{1+x}-\sqrt{x}}\)
Solution.

Question 30.
\(\int_{0}^{\frac{\pi}{4}} \frac{\sin x+\cos x}{9+16 \sin 2 x}\) dx
Solution.
Let I = \(\int_{0}^{\frac{\pi}{4}} \frac{\sin x+\cos x}{9+16 \sin 2 x}\) dx
Also, let sin x – cos x = t
⇒ (cos x + sin x) dx = dt
When x = 0, t= – 1 and when x =\(\frac{\pi}{4}\), t = 0
⇒ (sin x – cosx)² = t²
⇒ sin² x + cos² x – 2 sin x cos x = t²
⇒ 1 – sin 2x = t²
⇒ sin 2x = 1 – t²

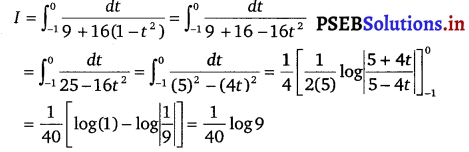
Question 31.
\(\int_{0}^{\frac{\pi}{2}}\) sin 2x tan^-1 (sin x) dx
Solution.
Let I = \(\int_{0}^{\frac{\pi}{2}}\) sin 2x tan^-1 (sin x) dx

= 2 \(\int_{0}^{\frac{\pi}{2}}\) sin x cos x tan^-1 (sin x) dx

Let sin x = t
cos dx = dt
when x = 0 , t = 0 and when x = \(\frac{\pi}{2}\), then t = 1

Question 32.
\(\int_{0}^{\pi} \frac{x \tan x}{\sec x+\tan x}\) dx
Solution.

Question 33.
\(\int_{1}^{4}\) [|x – 1| + |x – 2| + |x – 3|] dx
Solution.

Direction (34 – 39): Prove the following:

Question 34.
\(\int_{1}^{3} \frac{d x}{x^{2}(x+1)}=\frac{2}{3}+\log \frac{2}{3}\)
Solution.
Let I = \(\int_{1}^{3} \frac{d x}{x^{2}(x+1)}\)

Also, let \(\frac{1}{x^{2}(x+1)}=\frac{A}{x}+\frac{B}{x^{2}}+\frac{C}{x+1}\)

1 = Ax (x + 1) + B(x + 1) + C (x²)
1 = Ax²) + Ax + Bx + B + Cx²)
Equating the coefficients of x²), x and constant term, we get
A + C = 0;
A + B = 0;
B = 1
On solving these equations, we get
A = – 1; C = 1 and B = 1

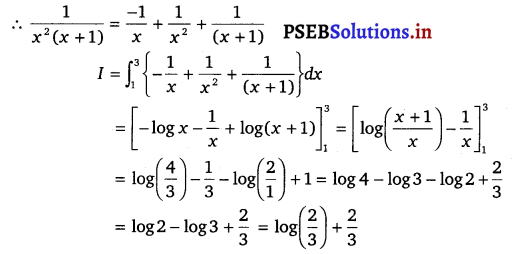
Hence, the given result is proved.

Question 35.
\(\int_{0}^{1}\) x e^x dx = 1
Solution.
Let I = \(\int_{0}^{1}\) x e^x dx dx
Integrating by parts, we get
I = \(x \int_{0}^{1} e^{x} d x-\int_{0}^{1}\left\{\left(\frac{d}{d x}(x)\right) \int e^{x} d x\right\}\) dx

= \(\left[x e^{x}\right]_{0}^{1}\) – \(\int_{0}^{1}\) e^x dx

= \(\left[x e^{x}\right]_{0}^{1}-\left[e^{x}\right]_{0}^{1}\)

= e – e + 1 = 1

Hence, the given result is proved.

Question 36.
\(\int_{-1}^{1}\) x¹⁷ cos⁴ x dx
Solution.
Let I = \(\int_{-1}^{1}\) x¹⁷ cos⁴ x dx
Also, f(x) = (- x)¹⁷ cos⁴ (- x)
= – x¹⁷ cos⁴ x = – f(x)
Therefore, f(x) is an odd function.
We know that if f(x) is an odd function, then \(\int_{-a}^{a}\) f(x) dx = o
∴ I = \(\int_{-1}^{1}\) x¹⁷ cos⁴ x dx = o
Hence, the given result is proved.

Question 37.
\(\int_{0}^{\frac{\pi}{2}}\) sin² x dx = \(\frac{2}{3}\)
Solution.
Let I = \(\int_{0}^{\frac{\pi}{2}}\) sin² x dx

= \(\int_{0}^{\frac{\pi}{2}}\) sin³ x sin x dx

= \(\int_{0}^{\frac{\pi}{2}}\) (1 – cos² x) sin x dx

= \(\int_{0}^{\frac{\pi}{2}}\) sin x dx – \(\int_{0}^{\frac{\pi}{2}}\) cos² x sin x dx

= \([-\cos ]_{0}^{\frac{\pi}{2}}+\left[\frac{\cos ^{3} x}{3}\right]_{0}^{\frac{\pi}{2}}\)

= \(1+\frac{1}{3}[-1]=1-\frac{1}{3}=\frac{2}{3}\)
Hence, the given result is proved.

Question 38.
\(\int_{0}^{\frac{\pi}{4}}\) 2 tan³ x dx = 1 – log 2
Solution.
Let I = \(\int_{0}^{\frac{\pi}{4}}\) 2 tan³ x dx

= 2 \(\int_{0}^{\frac{\pi}{4}}\) tan² x tan x dx

= 2 \(\int_{0}^{\frac{\pi}{4}}\) (sec² x – 1) tan x dx

= 2 \(\int_{0}^{\frac{\pi}{4}}\) sec² x tan x dx – 2 \(\int_{0}^{\frac{\pi}{4}}\) tan x dx
= \(2\left[\frac{\tan ^{2} x}{2}\right]_{0}^{\frac{\pi}{4}}+2[\log \cos x]_{0}^{\frac{\pi}{4}}\)

=1 + 2 [log cos \(\frac{\pi}{4}\) – log cos 0]
= 1 + 2 [log \(\frac{1}{\sqrt{2}}\) – log 1]
= 1 – log 2 – log 1
= 1 – log 2
Hence, the given result is proved.

Question 39.
\(\int_{0}^{1} \sin ^{-1} x d x=\frac{\pi}{2}-1\)
Solution.
Let I = \(\int_{0}^{1}\) sin^-1 x dx
= \(\int_{0}^{1}\) sin^-1 x . 1. dx

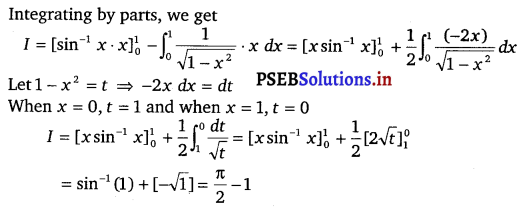
Hence, the given result is proved.

Question 40.
Eva1uate \(\int_{0}^{1}\) e^{2 – 3x} dx as a limit of a sum.
Solution.
Let I = \(\int_{0}^{1}\) e^{2 – 3x} dx
We know that,

Direction (41 – 44): Choose the correct answer:

Question 41.
\(\int \frac{d x}{e^{x}+e^{-x}}\) is equal to
(A) tan^-1 (e^x) + C
(B) tan^-1 (e^x) + C
(C) log (e^x – e^-x) + C
(D) log (e^x + e^-x) + C
Solution.
Let I = \(\int \frac{d x}{e^{x}+e^{-x}}\)
= ∫ \(\frac{e^{x}}{e^{2 x}+1}\) dx
Also, let e^x = t
⇒ e^x dx = dt
∴ I = ∫ \(\frac{d t}{1+t^{2}}\) tan^-1 t + C
= tan^-1 (e^x) + C
Hence, the correct answer is (A).

Question 42.
∫ \(\frac{\cos 2 x}{(\sin x+\cos x)^{2}}\) dx is equal to

(A) \(\frac{-1}{\sin x+\cos x}\)

(B) log |sin x + cos x| + C

(C) log |sin x – cos x| + C

(D) \(\frac{1}{(\sin x+\cos x)^{2}}\)
Solution.

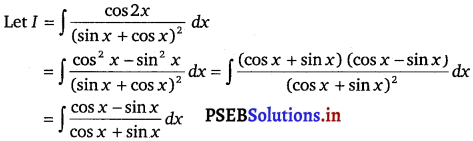
Let cos x + sin x = t
⇒ (cos x – sin x) dx = dt
∴ I = \(\int \frac{d t}{t}\)
= log |t| + C
= log |cos x+ sin x| + C
Hence, the correct answer is (B).

Question 43.
If f(a + b – x) = f(x), then \(\int_{a}^{b}\) x f(x) dx is equal to
(A) \(\frac{a+b}{2} \int_{a}^{b} f(b-x)\) dx

(B) \(\frac{a+b}{2} \int_{a}^{b} f(b+x)\) dx

(C) \(\frac{b-a}{2} \int_{a}^{b} f(x)\) dx

(D) \(\frac{b+a}{2} \int_{a}^{b} f(x)\) dx
Sol.
Let I = \(\int_{a}^{b}\) x f(x) dx …………….(i)
= \(\int_{a}^{b}\) (a + b – x) f (a + b – x) dx
[∵ \(\int_{a}^{b}\) f(x) dx = \(\int_{a}^{b}\) f(a + b – x) dx]
= \(\int_{a}^{b}\) (a + b – x) f(x) dx
⇒ I = (a + b) \(\int_{a}^{b}\) f(x) dx – I [Using Eq.(i)]
⇒ I = (a + b) \(\int_{a}^{b}\) f(x) dx
⇒ 2I = (a + b) \(\int_{a}^{b}\) f(x) dx
= \(\left(\frac{a+b}{2}\right) \int_{a}^{b} f(x) d x\)
Hence, the correct answer is (D).

Question 44.
The value of \(\int_{0}^{1} \tan ^{-1}\left(\frac{2 x-1}{1+x-x^{2}}\right)\) dx is
(A) 1
(B) 0
(C) – 1
(D) \(\frac{\pi}{4}\)
Solution.

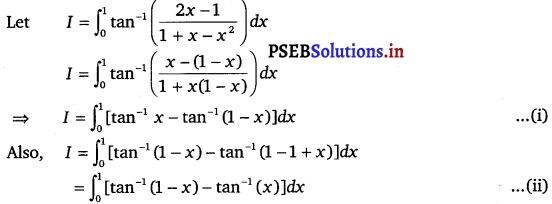
Adding Eqs. (i) and (ii), we get
2I = \(\int_{0}^{1}\) (tan^-1 x + tan^-1 (1 – x) – tan^-1 (1 – x) – tan^-1 x dx
⇒ 2I = 0
⇒ I = 0
Hence, the correct answer is (B).