PSEB 12th Class Maths Solutions Chapter 8 Application of Integrals Ex 8.1

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 8 Application of Integrals Ex 8.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 8 Application of Integrals Ex 8.1

Question 1.
Find the area of the region bounded by the curve y 2 = x and the lines x = 1, x = 4 and the x-axis in the first quadrant.
Solution.
The area of the region bounded by the curve, y² = x, the lines, x = 1 and x = 4 and the x-axis is the area ABCD.

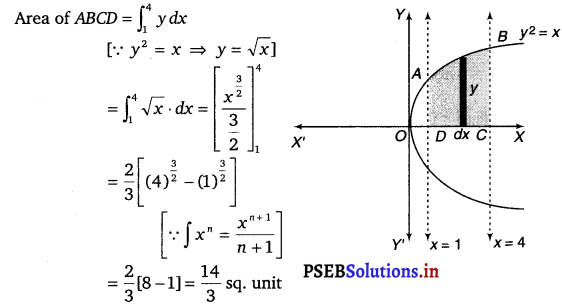
Question 2.
Find the area of the region bounded by y² = 9x, x = 2, x = 4 and the x-axis in the first quadrant.
Solution.
The area of the region bounded by the curve, y² = 9x, x = 2 and x = 4 and the x-axis is the area ABCD.

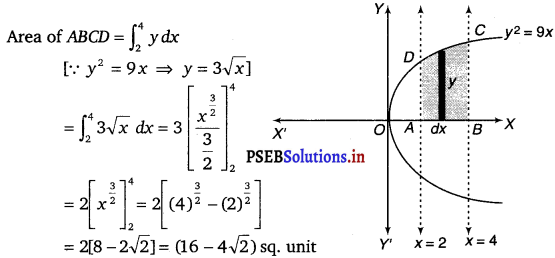
Question 3.
Find the area of the region bounded by x² – 4y, y – 2, y = 4 and the y-axis in the first quadrant.
Solution.
The area of the region bounded by the curve, x² = 4y, y = 2 and y = 4 and the y-axis is the area ABCD.

Question 4.
Find the area of the region bounded by the ellipse \(\frac{x^{2}}{16}+\frac{y^{2}}{9}\) = 1.
Solution.
The given equation of the ellipse is \(\frac{x^{2}}{16}+\frac{y^{2}}{9}\) = 1

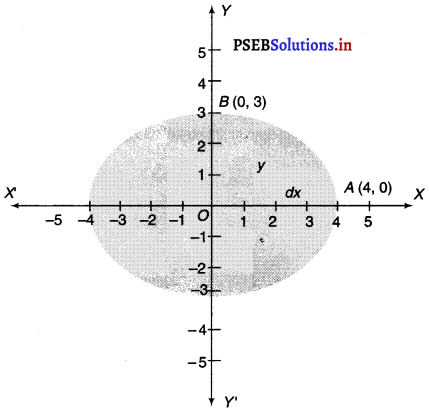
The given ellipse is symmetrical about both axes as it contains only even power of y and x.
Now, \(\frac{x^{2}}{16}+\frac{y^{2}}{9}\) = 1

\(\frac{y^{2}}{9}=1-\frac{x^{2}}{16}\)

y² = \(9\left(1-\frac{x^{2}}{16}\right)\)

y = ± 3 \(\sqrt{\left(1-\frac{x^{2}}{16}\right)}\)

Area bounded by ellipse = 4 × Area of OAB

Therefore, area bounded by the ellipse = 4 × 3π = 12π sq. unit.

Question 5.
Find the area of the region bounded by the ellipse \(\frac{x^{2}}{4}+\frac{y^{2}}{9}\) = 1
Solution.
The given equation of the ellipse can be represented as \(\frac{x^{2}}{4}+\frac{y^{2}}{9}\) = 1

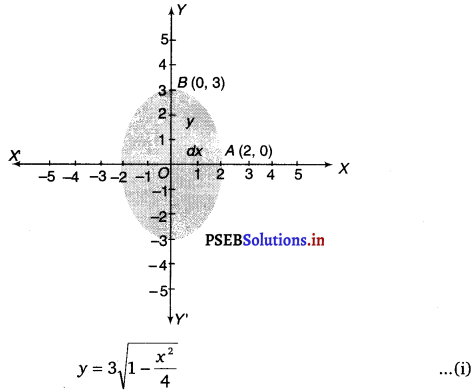
It can be observed that the ellipse is symmetrical about x-axis and y-axis.
∴ Area bounded by ellipse = 4 × Area of OAB
∴ Area of OAB = \(\int_{0}^{2}\) y dx

= \(\int_{0}^{2} 3 \sqrt{1-\frac{x^{2}}{4}}\) [Using EQuestion (i)]

= \(\frac{3}{2} \int_{0}^{2} \sqrt{4-x^{2}} d x=\frac{3}{2}\left[\frac{x}{2} \sqrt{4-x^{2}}+\frac{4}{2} \sin ^{-1} \frac{x}{2}\right]_{0}^{2}\)

= \(\frac{3}{2}\left[\frac{2 \pi}{2}\right]=\frac{3 \pi}{2}\)
Therefore, area bounded by the ellipse = 4 × \(\frac{3 \pi}{2}\) = 6π sq. unit

Question 6.
Find the area of the region in the first quadrant enclosed by x-axis, line x = √3y and the circle x² + y² = 4.
Solution.

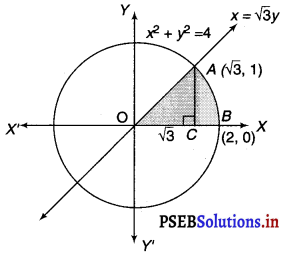
The area of the region bounded by the circle, x² + y² = 4, x = √3y, and the x-axis is the area OAB.
The point of intersection of the line and the circle in the first quadrant is (√3, 1).
Area of OAB = Area of ∆OCA + Area of ACB
Area of OAC = \(\frac{1}{2}\) × OC × AC
= \(\frac{1}{2}\) × √3 × 1
= \(\frac{\sqrt{3}}{2}\) …………..(i)

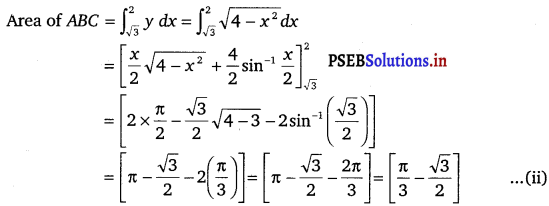
Therefore, are enclosed by x-axis, the line x = √3y, and the circle x² + y² = 4 in the first quadrant = \(\frac{\sqrt{3}}{2}+\frac{\pi}{3}-\frac{\sqrt{3}}{2}=\frac{\pi}{3}\) sq. unit

Question 7.
Find the area of the smaller part of the circle x² + y² = a² cut off by the line x = \(\frac{a}{\sqrt{2}}\).
Solution.
The area of the smaller part of the circle x² + y² = a², cut off the line, x = \(\frac{a}{\sqrt{2}}\), is the area ABCD.
It can be observed that the area of ABCD is symmetrical about x-axis.
∴ Area of ABCD = 2 × Area of ABC
Area of ABC = \(\int_{\frac{a}{\sqrt{2}}}^{a} y d x=\int_{\frac{a}{\sqrt{2}}}^{a} \sqrt{a^{2}-x^{2}} d x\)

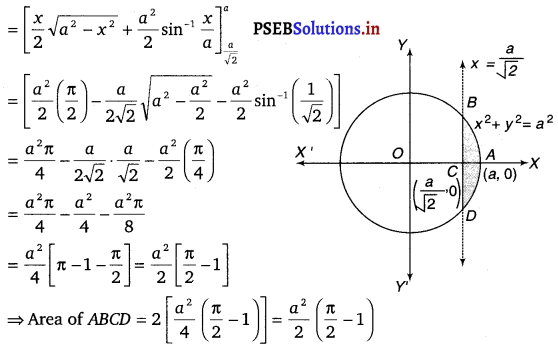
Therefore, the area of smaller part of the circle, x² + y² = a²,, cut off by the line, x = \(\frac{a}{\sqrt{2}}\), is \(\frac{a^{2}}{2}\left(\frac{\pi}{2}-1\right)\) sq. unit.

Question 8.
The area between x = y² and x = 4 is divided into two equal parts by the line x = a, find the value of a.
Solution.

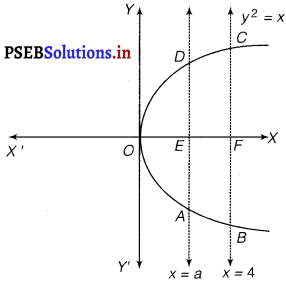
The line, x = a, divides the area bounded by the parabola and x = 4 into two equal parts.
∴ Area of OAD = Area of ABCD
It can be observed that the given area is symmetrical about x-axis.
⇒ Area of OED = Area of EFCD.
Area of OED = \(\int_{0}^{a}\) y dx = \(\int_{0}^{a}\) √x dx

⇒ 2 . \((a)^{\frac{3}{2}}\) = 8

⇒ \((a)^{\frac{3}{2}}\) = 4

⇒ a = \((4)^{\frac{3}{2}}\)

Therefore, the value of a is \((4)^{\frac{3}{2}}\) units.

Question 9.
Find the area of the region bounded by the parabola y = x and y = |x|.
Solution.

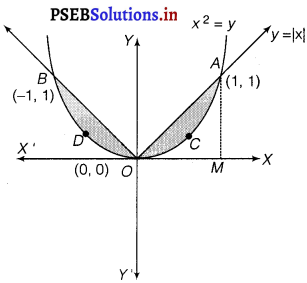
The area bounded by the parabola, x² = y and the line, y = |x| can be represented as in the given figure.
The given area is symmetrical about y-axis.
∴ Area of OACO = Area of ODBO
The point of intersection of (O O) parabola, x² = y, and line, y = x, is A(1, 1).
Area of OACO = Area of ∆OAB – Area of OBACO
∴ Area of OAB = \(\frac{1}{2}\) x OB x AB
= \(\frac{1}{2}\) × 1 × 1 = \(\frac{1}{2}\)
Area of OBACO = \(\int_{0}^{1}\) y dx = \(\int_{0}^{1}\) x² dx
= \(\left[\frac{x^{3}}{3}\right]_{0}^{1}=\frac{1}{3}\)
⇒ Area of OACO = Area of ∆OAB – Area of OBACO
= \(\frac{1}{2}-\frac{1}{3}=\frac{1}{6}\)
Therefore, the required area = 2 \(\left[\frac{1}{6}\right]=\frac{1}{3}\) sq. units.

Question 10.
Find the area hounded by the curve xx² = 4y and the line x = 4y – 2.
Solution.
The area bounded by the curve, xx² = 4y and line, x = 4y – 2, is represented by the shaded area OBAQ.
Let A and B be the points of intersection of the line and parabola.
Coordinates of point A are (- 1, \(\frac{1}{4}\))
Coordinates of point B are (2, 1).
We draw AL and BM perpendicular to x-axis.
It can be observed that,
Area of OBAO = Area of OBCD + Area of OACO ………….(i)
Then, Area of OBCO = Area of OMBC – Area of OMBO
= \(\int_{0}^{2} \frac{x+2}{4} d x-\int_{0}^{2} \frac{x^{2}}{4} d x\)

= \(\frac{1}{4}\left[\frac{x^{2}}{2}+2 x\right]_{0}^{2}-\frac{1}{4}\left[\frac{x^{3}}{3}\right]_{0}^{2}\)

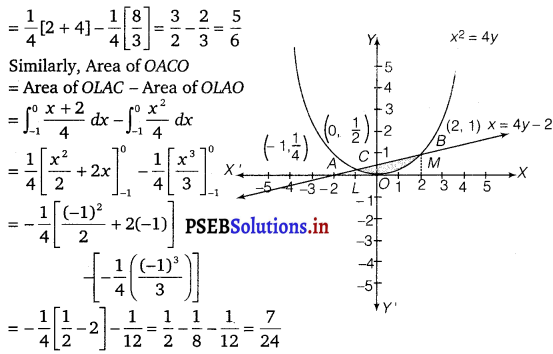
Therefore, required area = \(\left(\frac{5}{6}+\frac{7}{24}\right)=\frac{9}{8}\) sq. unit.

Question 11.
Find the area of the region bounded by the curve y² = 4x and the line x – 3.
Solution.
The region bounded by the parabola, y² = 4x and the line, x = 3, is the area OACO.

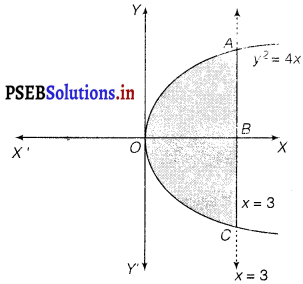
The area OACO is symmetrical about x-axis.
∴ Area of OACO = 2 (Area of OAB)
Area of OACO = 2[\(\int_{0}^{3}\) y dx]
[∵ y² = 4x
⇒ y = 2√x]
= 2 \(\int_{0}^{3}\) 2√x dx

= 4 \(\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_{0}^{3}\)

= \(\frac{8}{3}\left[(3)^{\frac{3}{2}}\right]\)

= 8√3

Direction (12 – 13): Choose the correct answer:

Question 12.
Area lying in the first quadrant and bounded by the circle x² + y² = 4 and the lines x = 0 and x = 2 is.
(A) π
(B) \(\frac{\pi}{2}\)

(C) \(\frac{\pi}{3}\)

(D) \(\frac{\pi}{4}\)
Solution.
The area bounded by the circle and the lines, x = 0 and x = 2, in the first quadrant is represented as given in the figure.

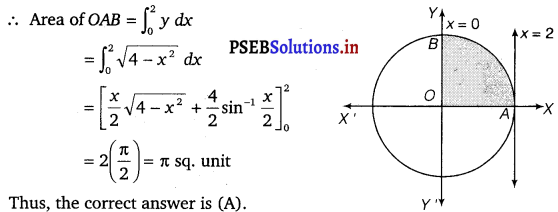
Question 13.
Area of the region bounded by the curve y² = 4x, y-axis and the line y = 3 is
(A) 2

(B) \(\frac{9}{4}\)

(C) \(\frac{9}{3}\)

(D) \(\frac{9}{2}\)
Solution.
The area bounded by the curve y² = 4x, y-axis and y = 3 is represented as

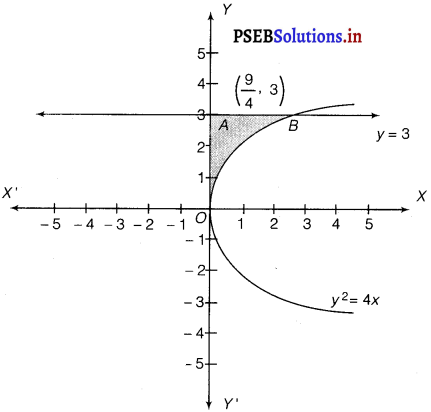
Area of OAB = \(\int_{0}^{3}\) x dy
[∵ y² = 4x
⇒ x = \(\frac{y^{2}}{4}\)]

= \(\int_{0}^{3} \frac{y^{2}}{4} d y=\frac{1}{4}\left[\frac{y^{3}}{3}\right]_{0}^{3}\)

= \(\frac{1}{12}(27)=\frac{9}{4}\) sq unit.

Thus, the correct answer is (B).