PSEB 12th Class Maths Solutions Chapter 8 Application of Integrals Ex 8.2

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 8 Application of Integrals Ex 8.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 8 Application of Integrals Ex 8.2

Question 1.
Find the area of the circle 4x² + 4y² = 9 which is interior to the parabola x² = 4y.
Solution.
The required area is represented by the shaded area OBCDO.

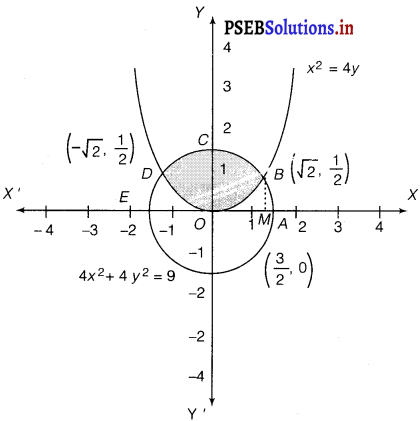
Solving the given equation of circle, 4x² + 4 y² = 9 and parabola x² = 4y, we get the point of intersection as B \(\left(\sqrt{2}, \frac{1}{2}\right)\) and D \(-\left(\sqrt{2}, \frac{1}{2}\right)\).

It can be observed that the required area is symmetrical about y-axis.
∴ Area of OBCDO = 2 × Area of OBCO
We draw BM perpendicular to OA.
Therefore, the coordiantes of M are (√2, 0).
Therefore, Area of OBCO = Area of OMBCO – Area of OMBO

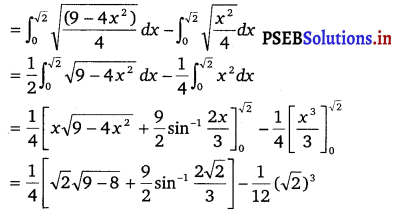
Question 2.
Find the area bounded by curves (x – 1)² + y² = 1 and x² + y² = 1.
Solution.

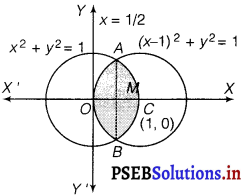
The area bounded by the curves, (x – 1)² + y² = 1 and x² + y² = 1 represented by the shaded area as given in the figure.

On solving these equations, (x – 1)² + y² = 1 and x² + y² = 1, we get the point of intersection as A \(\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)\) and B \(\left(\frac{1}{2},-\frac{\sqrt{3}}{2}\right)\)

It can be observed that the required area is symmetrical about x-axis.

∴ Area of OBCAO = 2 × Area of OCAO
We join AB, which intersects OC at M, such that AM is perpendicular to OC.
The coordinates of M are (\(\frac{1}{2}\), o)
⇒ Area of OCAO = Area of OMAO + Area of MCAM

Question 3.
Find the area of the region bounded by the curves y = x² + 2, y = x, x = 0 and x = 3.
Solution.
The area bounded by the curves, y = x², y – x, x – 0 and x = 3, is represented by the shaded area OCBAO as
Area of OCBAO = Area of ODBAO – Area of ODCO

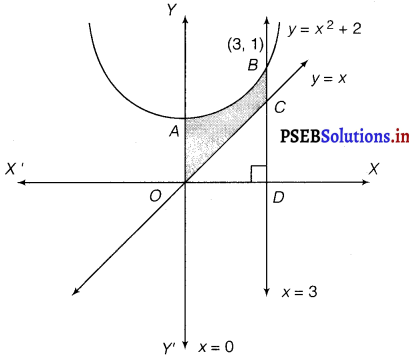
Area of OCBAO = Area of ODBAO – Area of ODCO
= \(\int_{0}^{3}\) (x² + 2) dx – \(\int_{0}^{3}\) x dx

= \(\left[\frac{x^{3}}{3}+2 x\right]_{0}^{3}-\left[\frac{x^{2}}{2}\right]_{0}^{3}=[9+6]-\left[\frac{9}{2}\right]\)

= \(15-\frac{9}{2}=\frac{21}{2}\) sq. unit.

Question 4.
Using integration, find the area of region bounded by the triangle whose vertices are (- 1, 0), (1, 3) and (3, 2).
Solution.

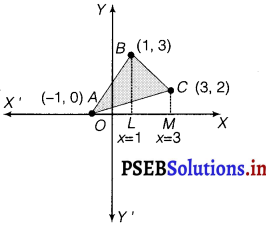
BL and CM are drawn perpendicular to x-axis.
It can be observed in the given figure that,
Area of ∆ACB = Area of ALBA +Area of BLMCB – Area of AMCA …………(i)
Equation of the line joining points (x₁, y₁) and (x₂, y₂) is
y – y₁ = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\) (x – x₁)
Equation of line segment AB is
y – 0 = \(\frac{3-0}{1+1}\) (x + 1)

⇒ y = \(\frac{3}{2}\) (x + 1)

∴ Area of ALBA = \(\int_{-1}^{1} \frac{3}{2}(x+1)\) dx

= \(\frac{3}{2}\left[\frac{x^{2}}{2}+x\right]_{-1}^{1}=\frac{3}{2}\left[\frac{1}{2}+1-\frac{1}{2}+1\right]\)
= 3 unit

Therefore, from equation (i), we get
Area of ∆MBC = (3 + 5 – 4) = 4 sq. unit.

Question 5.
Using integration, find the area of the triangular region whose sides have the equations y = 2x + 1, y = 3x + 1 and x = 4.
Solution.

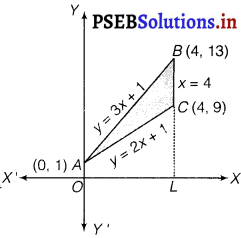
The equations of sides of the triangle y are y = 2x + 1, y = 3x + 1 and x = 4.
On solving these equations, we get the vertices of triangle as A(0, 1), B(4, 13) and C(4, 9).
It can be observed that,
Area of ∆ACB = Area of OLBAO – Area of OLCAO
= \(\) (3x + 1) dx – \(\) (2x + 1) dx

= \(\left[\frac{3 x^{2}}{2}+x\right]_{0}^{4}\) – \(\left[\frac{2 x^{2}}{2}+x\right]_{0}^{4}\)
=(24 + 4) – (16 + 4)
= 28 – 20 = 8 sq. unit.

Direction (6 – 7): Choose the correct answer:

Question 6.
Smaller area enclosed by the circle x² + y² = 4 and the line x + y = 2 is
(A) 2 (π – 2)
(B) π – 2
(C) 2π – 1
(D) 2 (π + 2)
Solution.
The smaller area enclosed by the circle, x² + y² – 4 and the line, x + y = 2, is represented by the shaded area ACBA as given in the figure.
It can be observed that,

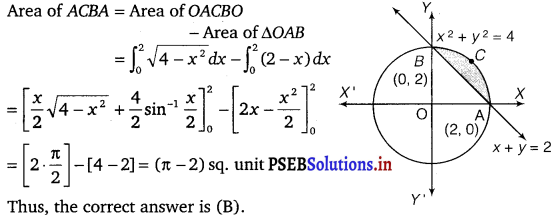
Question 7.
Area lying between the curves y² = 4x and y = 2x is
(A) \(\frac{2}{3}\)

(B) \(\frac{1}{3}\)

(C) \(\frac{1}{4}\)

(D)\(\frac{3}{4}\)
Solution.
The area lying between the curve, y² = 4x and y = 2x, is represented by the shaded area OBAO as given in the figure.
The points of intersection of these, curves are O (0, 0) and A(1, 2).
We draw AC perpendicular to x-axis such that the coordinates of C are (1, 0).
∴ Area of OBAO = Area of ∆OCA – Area of OCABO
= \(\int_{0}^{1}\) 2x dx – \(\int_{0}^{1}\) 2 √x dx

= \(2\left[\frac{x^{2}}{2}\right]_{0}^{1}-2\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_{0}^{1}\)

= |1 – \(\frac{4}{3}\)|

= |- \(\frac{1}{3}\)| = \(\frac{1}{3}\)