PSEB 12th Class Maths Solutions Chapter 8 Application of Integrals Miscellaneous Exercise

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 8 Application of Integrals Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 8 Application of Integrals Miscellaneous Exercise

Question 1.
Find the area under the given curves and given lines.
(i) y = x², x = 1, x = 2 and x – axis
(ii) y = x⁴, x = 1, x = 5 and x – axis
Solution.

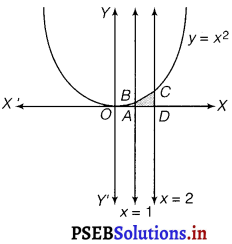
(i) The required area is represented by the shaded area ADCBA as
Area of ADCBA = \(\int_{1}^{2}\) y dx

= \(\int_{1}^{2}\) x² dx

= \(\left[\frac{x^{3}}{3}\right]_{1}^{2}=\frac{8}{3}-\frac{1}{3}=\frac{7}{3}\) sq. unit.

(ii)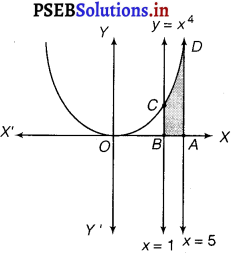

The required area is represented by y the shaded area ADCBA as

Area of ADCBA = \(\int_{1}^{5}\) x⁴ dx = \(\)
= \(\frac{(5)^{5}}{5}-\frac{1}{5}\)

= \((5)^{4}-\frac{1}{5}\)

= 625 – \(\frac{1}{5}\)

=624.8 sq.unit.

Question 2.
Find the area between the curves, y = x and y = x².
Solution.
The required area is represented by the shaded area OBADO as

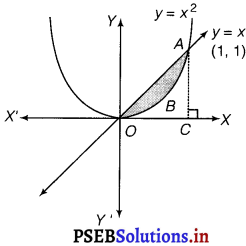
The points of intersection of the curves, y = x and y = x² ,is A(1,1).
We draw AC perpendicular to x-axis.
∴ Area of OBAO = Area of AOCA – Area of OCABO ……….. (i)
= \(\int_{0}^{1}\) x dx – \(\int_{0}^{1}\) x² dx

= \(\left[\frac{x^{2}}{2}\right]_{0}^{1}-\left[\frac{x^{3}}{3}\right]_{0}^{1}\)

= \(\frac{1}{2}-\frac{1}{3}=\frac{1}{6}\) sq. unit.

Question 3.
Find the area of the region lying in the first quadrant and bounded by y = 4x², x = 0, y = 1 and y = 4.
Solution.
The area in the first quadrant bounded by y = 4x², x = 0, y = 1 and y = 4 is represented by the shaded area ABCDA as given in the figure.

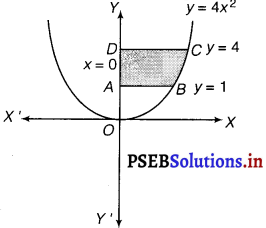
∴ Area of ABCD = \(\int_{1}^{4}\) x dx
[∵ y = 4x²
⇒ x = \(\frac{\sqrt{y}}{2}\)]

= \(\int_{1}^{4} \frac{\sqrt{y}}{2} d x\)

= \(\frac{1}{2}\left[\frac{y^{\frac{3}{2}}}{\frac{3}{2}}\right]_{1}^{4}\)

= \(\frac{1}{3}\) [(4)^{\(\frac{3}{2}\) – 1]}

= \(\frac{1}{3}\) [8 – 1]

= \(\frac{7}{3}\) sq unit.

Question 4.
Sketch the graph of y = |x + 3| and evaluate \(\int_{-6}^{0}\) |x + 3| dx.
Solution.
The given equation is y = |x + 3|
The corresponding values of x and y are given in the following table.

On plotting these, points, we get the graph of y = |x + 3| as follows.

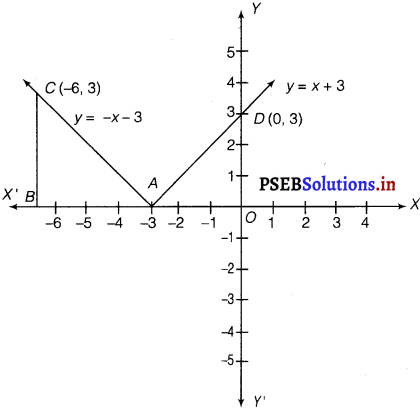
We know that, (x + 3) ≤ 0 for – 6 ≤ x – 3 and (x + 3) ≥ 0 for – 3 ≤ x ≤ 0

Question 5.
Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
Solution.
The graph of y = sin x can be drawn as

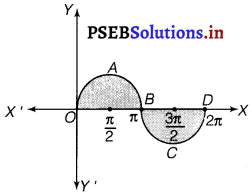
∴ Required area = Area of OABO + Area of BCDB
= \(\int_{0}^{\pi}\) sin x dx + |\(\int_{0}^{2 \pi}\) sin x| dx

= \([-\cos x]_{0}^{\pi}+\left|[-\cos x]_{\pi}^{2 \pi}\right|\)

= [- cos π + cos 0] + |- cos 2π + cos π|
= 1 + 1 + |(- 1 – 1)|
= 2 + |- 2|
= 2 + 2 = 4 sq. unit

Question 6.
Find the area enclosed between the parabola y² = 4ax and the line y = mx.
Solution.
The area enclosed between the parabola, y² = 4ax and the line, y = mx, is represented by the shaded area OABO as given in the figure

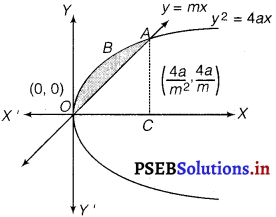
The points of intersection of both the curves are (0, 0) and \(\left(\frac{4 a}{m^{2}}, \frac{4 a}{m}\right)\).

We draw AC perpendicular to x-axis.
∴ Area of OABO = Area of OCABO -Area of ∆OCA

Question 7.
Find the area enclosed by the parabola 4y = 3x² and the line 2y = 3x + 12.
Solution.
The area enclosed between the parabola, 4y = 3x² and the line, 2y = 3x +12 is represented by the shaded area OBAO as

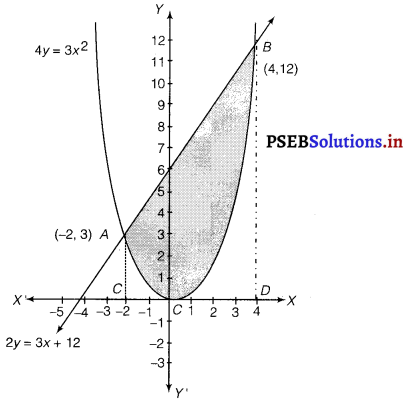
The points of intersection of the given curves are A(- 2, 3) and (4, 12).
We draw AC and BD perpendicular to x-axis.
Area of OBAO = Area of CDBA – (Area of ODBO + Area of OACO).
= \(\int_{-2}^{4} \frac{1}{2}(3 x+12) d x-\int_{-2}^{4} \frac{3 x^{2}}{4} d x\)

= \(=\frac{1}{2}\left[\frac{3 x^{2}}{2}+12 x\right]_{-2}^{4}-\frac{3}{4}\left[\frac{x^{3}}{3}\right]_{-2}^{4}\)

= \(\frac{1}{2}\) [24 + 48 – 6] – \(\frac{1}{4}\) [64 + 8]

=\(\frac{1}{2}\) [90] – \(\frac{1}{4}\) [72]
= 45 – 18 = 27 sq. unit.

Question 8.
Find the area of the smaller region hounded by the ellipse \(\frac{x^{2}}{9}+\frac{y^{2}}{4}\) = 1 and the line \(\frac{x}{3}+\frac{y}{2}\) = 1.
Solution.
The area of the smaller region bounded by the ellipse, \(\frac{x^{2}}{9}+\frac{y^{2}}{4}\) = 1 and the line, \(\frac{x}{3}+\frac{y}{2}\) = 1, is represented by the shaded region BCAB as

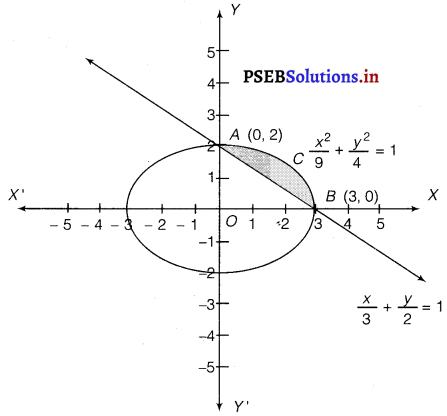
∴ Area of BCAB = Area of OBCAO – Area of OBAO

= \(\int_{0}^{3} 2 \sqrt{1-\frac{x^{2}}{9}} d x-\int_{0}^{3} 2\left(1-\frac{x}{3}\right) d x\)

= \(\frac{2}{3}\left[\int_{0}^{3} \sqrt{9-x^{2}} d x\right]-\frac{2}{3} \int_{0}^{3}(3-x) d x\)

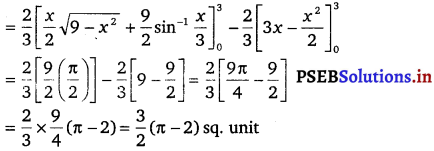
Question 9.
Find the area of the smaller region bounded by the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 and the line \(\frac{x}{a}+\frac{y}{b}\) = 1.
Solution.
The area of the smaller region bounded by the ellipse, \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1, and the line, \(\frac{x}{a}+\frac{y}{b}\) = 1, is represented by the shaded region BCAB as

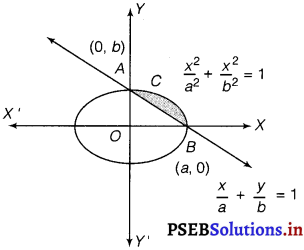
∴ Area of BCAB = Area of OBCAO – Area of OBAO

Question 10.
Find the area of the region enclosed by the parabola x² = y, the line y = x + 2 and x- axis.
Solution.
We have x² = y.
It represents a parabola with vertex at (0, 0), axis along the positive direction of y-axis and it open upwards.
Also, y = x + 2 represents a straight line cutting x – axis at (- 2, 0)
Solving x² = y and y = x + 2, we get

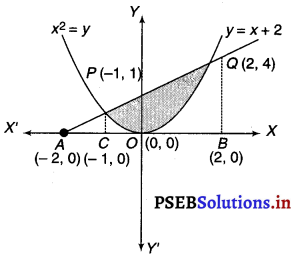
x² = x + 2
=> x² – x – 2 = 0
=> (x – 2)(x + 1) = 0
x = 2, x = -1
When x = 2, y = (2)² = 4
So the two curves x² = y and y = x + 2 intersect at the points (2, 4) and (- 1, 1)
∴ Required area = Shaded region shown in the figure
= \(\int_{-1}^{2}\) (x + 2 – x²) dx

= \(\left[\frac{x^{2}}{2}+2 x-\frac{x^{3}}{3}\right]_{-1}^{2}\)

= \(\frac{1}{2}\) (4 – 1) + 2 (2 – 1) – \(\frac{1}{3}\) (8 + 1)

= \(\frac{3}{2}\) + 6 – 3

= \(\frac{3}{2}\) + 3 = \(\frac{9}{2}\) sq. unit.

Question 11.
Using the method of integration find the area bounded by the curve |x| + |y| = 1.
[Hint: The required region is bounded by lines x + y = 1, x – y = 1, – x + y = 1 and – x – y = 1.]
Solution.
The given curve is |x| + |y| = 1

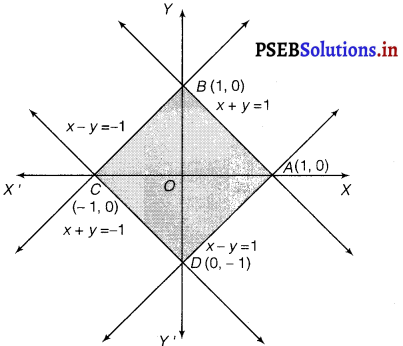
In first quadrant, (x > 0, y > 0)
Then, the line AB is x + y = 1
In second quadrant, (x < 0, y > 0)
Then, the line BC is – x + y = 1
In third quadrant, (x < 0, y < 0) Then, the line CD is -x – y = 1 In fourth quadrant, (x > 0, y < 0)
Then, the line DA is x – y = 1
Since, ABCD is a square.
∴ Area of ADCB = 4 × Area of OBAO
= 4 \(\int_{0}^{1}\) (1 – x) dx
= 4 \(\left(x-\frac{x^{2}}{2}\right)_{0}^{1}\)
= 4 [1 – \(\frac{1}{2}\)]
= 4 \(\frac{1}{2}\) = 2 sq. unit.

Question 12.
Find the area bounded by curves {(x, y) : y ≥ x² and y = |x|}.
Solution.

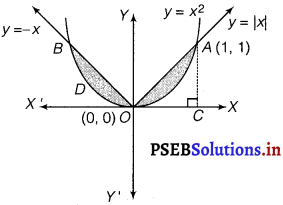
The area bounded by the curves {(x, y): y > x² and y = |x|}, is represented by the shaded region as It can be observed that the required area is symmetrical about y-axis.
∴ Required area = 2 [Area of OCAO – Area of OCADO]
= 2 [\(\int_{0}^{1}\) x dx – \(\int_{0}^{1}\) x² dx]

= \(2\left[\left[\frac{x^{2}}{2}\right]_{0}^{1}-\left[\frac{x^{3}}{3}\right]_{0}^{1}\right]\)

= \(2\left[\frac{1}{2}-\frac{1}{3}\right]=2\left[\frac{1}{6}\right]=\frac{1}{3}\) sq unit.

Question 13.
Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A (2, 0), B (4, 5) and C (6, 3).
Solution.
The vertices of AABC are A (2, 0), B(4, 5) and C( 6, 3).

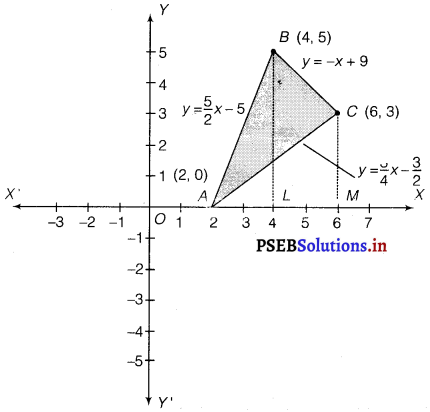
Equation of line segment AB is
y – 0 = \(\frac{5-0}{4-2}\) (x – 2)
⇒ 2y = 5x – 10
⇒ y = \(\frac{5}{2}\) (x – 2) …………..(i)
Equation of line segment BC is
y – 5 = \(\frac{3-5}{6-4}\) (x – 4)
⇒ 2y – 10 = – 2x + 8
⇒ 2y = – 2x + 18
y = – x + 9 ………………(ii)
Equation of line segment CA is
y – 3 = \(\frac{3-5}{6-4}\) (x – 6)
⇒ – 4y + 12 = – 3x + 18
4y = 3x – 6
⇒ y = \(\frac{3}{4}\) (x – 2) …………….(iii)
Area of ∆ABC = Area of ABLA + Area of BLMCB – Area of ACMA
= \(\int_{2}^{4} \frac{5}{2}(x-2) d x+\int_{4}^{6}(-x+9) d x-\int_{2}^{6} \frac{3}{4}(x-2) d x\)

= \(\frac{5}{2}\left[\frac{x^{2}}{2}-2 x\right]_{2}^{4}+\left[\frac{-x^{2}}{2}+9 x\right]_{4}^{6}-\frac{3}{4}\left[\frac{x^{2}}{2}-2 x\right]_{2}^{6}\)

= \(\frac{5}{2}\) [8 – 8 – 2 + 4] + [- 18 + 54 + 8 – 36] – \(\frac{3}{4}\) [18 – 12 – 2 + 4]
= 5 + 8 – \(\frac{3}{4}\) (8)
= 13 – 6 = 7 sq. unit.

Question 14.
Using the method of integration, find the area of the region bounded by lines:
2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
Solution.
The given equations of lines are
2x + y = 4 ……………..(i)
3x – 2y = 6 …………….(ii)
and x-3y + 5 = 0 ………….(iii)

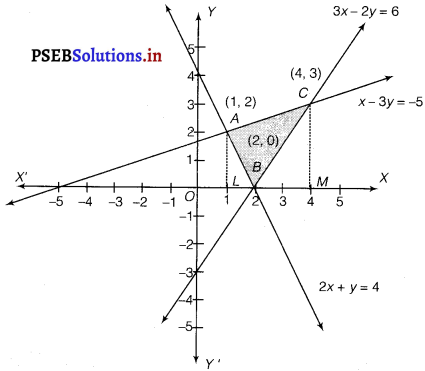
The area of the region bounded by the lines is the area of AABC. AL and CM are the perpendiculars on x-axis.
Area of ∆ABC = Area of ALMCA – Area of ALB – Area of CMB

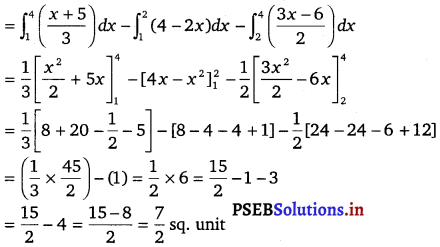
Question 15.
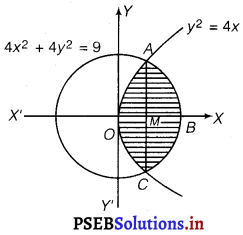
Find the area of the region 4(x, y): y² ≤ 4x, 4x² + 4y² ≤ 9}.
Solution.
y² = 4x is a paraola whose vertex is the origin and 4x² + 4y² = 9 represents circle whose centre is (0, 0) 4x² + 4y² = 9 and radius = \(\frac{3}{2}\)
On solving y² = 4x and x² + y² = \(\frac{9}{4}\)

The points of intersection are A\(\left(\frac{1}{2}, \sqrt{2}\right)\) and C\(\left(\frac{1}{2}, -\sqrt{2}\right)\).
Both the curves are symmetrical about x-axis.
∴ Required area = area of the shaded region
= 2 (area of the region OBAO)
= 2 [(area of the region OMAO) + (area of the region MBAM)]

Direction (16 – 19): Choose the correct answer.

Question 16.
Area bounded by the curve y = x², the x-axis and the ordinates x = – 2 and x = 1 is
(A) – 9

(B) \(-\frac{15}{4}\)

(C) \(\frac{15}{4}\)

(D) \(\frac{17}{4}\)
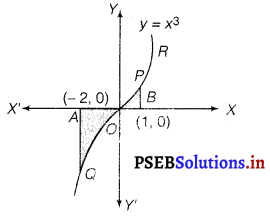
Solution.

The curve is y = x³
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = 3x²
∴ Curve is an increasing curve
\(\frac{d y}{d x}\) = 0, x = 0 dx
∴ x-axis is the tangent at x = 0
f(- x) = – f(x)
⇒ (- x)³ = – x³
Curve is symmetrical in opposite quadrants.
Area bounded by the curve y = x³, the x- axis, x = Area of the region AQOBPOA
= Area of the region AQOA + Area of the region ABPO

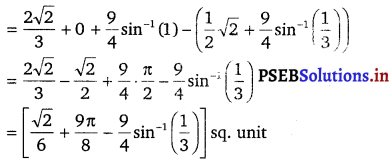
Thus, the correct answer is (D).

Question 17.
The area bounded by the curve y = x |x|, x-axis and the ordinates x =1 and x = 1 is given by
(A) 0
(B) \(\frac{1}{3}\)

(C) \(\frac{2}{3}\)

(D) \(\frac{4}{3}\)
[Hint: y = x² if x > 0 and y = – x² if x < 0]
Solution.
Required area = \(\int_{-1}^{1}\) y dx
= \(\int_{-1}^{1}\) x |x| dx

= \(\int_{-1}^{0}\) x² dx + \(\int_{0}^{1}\) x² dx

= \(\left[\frac{x^{3}}{3}\right]_{-1}^{0}+\left[\frac{x^{3}}{3}\right]_{0}^{1}\)

= \(-\left(-\frac{1}{3}\right)+\frac{1}{3}=\frac{2}{3}\) sq. units
Thus, the correct answer is (C).

Question 18.
The area of the circle x² + y² = 16 exterior to the parabola y² = 6x is
(A) \(\frac{4}{3}\) (4π – √3)

(B) \(\frac{4}{3}\) (4π + √3)

(C) \(\frac{4}{3}\) (8π – √3)

(D) \(\frac{4}{3}\) (8π + √3)
Sol.
The given equations are
x² + y² = 16 …………..(i)
y² = 6x …………(ii)

Area ounded by the circle and parabola = 2 [Area of OADO + Area of ADBA]

= 2 \(\left[\int_{0}^{2} \sqrt{16} x d x+\int_{2}^{4} \sqrt{16-x^{2}} d x\right]\)

= \(2\left[\sqrt{6}\left\{\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right\}_{0}^{2}\right]+2\left[\frac{x}{2} \sqrt{16-x^{2}}+\frac{16}{2} \sin ^{-1} \frac{x}{4}\right]_{2}^{4}\)
Area of circle = π(r)²
= π(4)²
= 16π sq unit
Required area = 16π – \(\frac{4}{3}\) [4π + V3]
= \(\frac{4}{3}\) [4 × 3π – 4π – √3]
= \(\frac{4}{3}\) (8π – √3) sq. unit
Thus, the correct answer is (C).

Question 19.
The area bounded by the y – axis, y = cos x and y = sin x, when 0 ≤ x < \(\frac{\pi}{2}\) is
(A) 2 (√2 – 1)
(B) √2 – 1
(C) √2 + 1
(D) √2
Solution.
The two curves y = sin x and y = cos x meet where sin x = cos x, i.e., where tan x = 1.

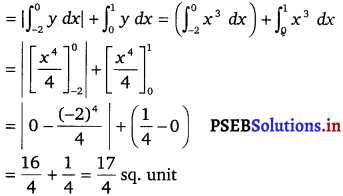
∴ Required area (shown in shaded region) = \(\int_{0}^{\pi / 4}\) (cos x – sinx) dx
= \([\sin x+\cos x]_{0}^{\pi / 4}\)

= sin \(\frac{\pi}{4}\) + cos \(\frac{\pi}{4}\) – (0 + 1)

= \(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\) – 1

= \(\frac{2}{\sqrt{2}}\) – 1
= √2 – 1
Thus, the correct answer is (B).