PSEB 12th Class Maths Solutions Chapter 9 Differential Equations Ex 9.2

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter Differential Equations Ex 9.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.2

Direction (1 – 10): In each of the questions verify that the given function (explicit or implicit) is a solution of the corresponding differential equation.

Question 1.
y = e^x + 1 ; y” – y’ = 0 ,
Solution.
Given, y = e^x + 1
Differentiating both sides of this equation w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (e^x + 1)
⇒ y’ = e^x
Now, differentiating equation (i) w.r.t. x, we get
\(\frac{d}{d x}\) (y’) = \(\frac{d}{d x}\) (e^x)
⇒ y” = e^x
Substituting the values of y’ and y” in the given differential equation, we get the L.H.S. as
y” – y’ = e^x – e^x = 0 = R.H.S.
Thus, the given function in the solution of the corresponding differential equation.

Question 2.
y = x² + 2x + C : y’ – 2x – 2 = 0
Solution.
Given, y = x² + 2x + C
Differentiating both sides of this equation w.r.t x, we get
y’ = \(\frac{d}{d x}\) (x² + 2x + C)
⇒ y’ = 2x+2 ax
Substituting the value of y’ in the given differential equation, we get
L.H.S. = y’ – 2x – 2 = 2x + 2 – 2x – 2 = 0 = R.H.S.
Hence, the given function is the solution of the corresponding differential equation.

Question 3.
y = cos x + C: y’ + sin x – 0
Solution.
Given, y = cos x + C
Differentiating both sides of this equation w.r.t. x, we get
y’ = \(\frac{d}{d x}\) (cos x + C)
=> y’ = – sin x dx
Substituting the value of y in the given differential equation, we get
L.H.S. y’ + sin x = – sin x + sin x = 0 = R.H.S.
Hence, the given function is the solution of the corresponding differential equation.

Question 4.
y = \(\sqrt{1-x^{2}}\); y’ = \(\frac{x y}{1+x^{2}}\)
Solution.
Given, y = \(\sqrt{1-x^{2}}\)
Differentiating both sides of this equation w.r.t. x, we get

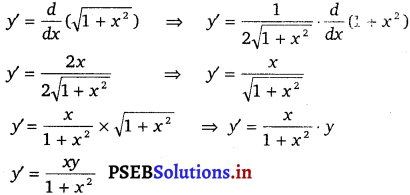
∴ L.H.S. = R.H.S.
Hence, the given function is the solution of the corresponding differential equation.

Question 5.
y = Ax: xy’ = y, (x ≠ 0)
Solution.
Given, y = Ax
Differentiating both sides of this equation w.r.t. x, we get
y = -^-G4x) =^y = A
ax
Substituting the value of y’ in the given differential equation, we get
L.H.S. = xy’ = x . A = Ax = y= R.H.S.
Hence, the given function is the solution of the corresponding differential equation.

Question 6.
y = x sin x : xy’ = y + x \(\sqrt{x^{2}-y^{2}}\) (x ≠ 0 and x > y or x< – y)
Solution.
Given, y = x sin x
Differentiating both sides of this equation w.r.t. x, we get
y’ = \(\frac{d}{d x}\) (x sin x)
y’ = sin x . \(\frac{d}{d x}\) (x) + x . \(\frac{d}{d x}\) (sin x)
⇒ y = sin x + x cos x
Substituting the values of y in the given differential equation, we get
L.H.S. = xy = x (sin x + x cos x)
= x sin x + x² cos x
= y + x² . \(\sqrt{1-\sin ^{2} x}\)
= y + x² \(\sqrt{1-\left(\frac{y}{x}\right)^{2}}\)
= y + x \(\sqrt{y^{2}-x^{2}}\) = R.H.S
Hence, the given function is the solution of the corresponding differential equation.

Question 7.
xy = log y + C : y’ = \(\frac{y^{2}}{1-x y}\) (xy ≠ 1)
Solution.
Given, xy = log y + C
Differentiating both sides of this equation w.r.t. x, we get
\(\frac{d}{d x}\) (xy) = \(\frac{d}{d x}\) (log y)
⇒ y . \(\frac{d}{d x}\) (x) + x . \(\frac{d y}{d x}\) = \(\frac{1}{y}\) \(\frac{d y}{d x}\)
⇒ y + xy’ = \(\frac{1}{y}\) y’
⇒ y² + xy y’ = y’
⇒ (xy – 1) y’ = – y²
⇒ y’ = \(\frac{y^{2}}{1-x y}\)
.-. L.H.S. = R.H.S.
Hence, the given function is the solution of the corresponding differential equation.

Question 8.
y – cos y = x : (y sin y + cos y + x) y’ = y
Solution.
Given, y – cos y = x …………(i)
Differentiating both sides of this equation w.r.t. x, we get
\(\frac{d y}{d x}\) – \(\frac{d}{d x}\) (cos y) = \( \frac{d y}{d x} (x)\)
⇒ y’ + sin y . y’ = 1
⇒ y’ (1 + sin y) = 1
⇒ y’ = \(\frac{1}{1+\sin y}\)
Substituting the value of y in equation, we get
L.H.S = (y sin y + cos y + x) y’
= (y sin y + cos y + y – cos y) × \(\frac{1}{1+\sin y}\)
= y (1 + sin y) \(\frac{1}{1+\sin y}\)
= y = R.H.S.
Hence, the given function is the solution of the corresponding differential equation.

Question 9.
x + y = tan^-1 y : y² y’ + y² + 1 = 0
Solution.
Given, x + y = tan^-1 y
Differentiating both sides of this equation w.r.t. x, we get

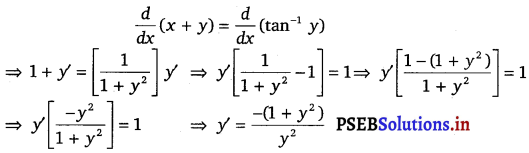
Substituting the values of y’ in the given differential equation, we get
L.H.S = y² y’ + y² + 1
= y² \(\left[\frac{-\left(1+y^{2}\right)}{y^{2}}\right]\) + y² + 1
= – 1 – y² + y² + 1 = 0
= R.H.S
Hence, the given function is the solution of the corresponding differential equation.

Question 10.
y = \(\sqrt{a^{2}-x^{2}}\), x ∈ (- a, a): x + y \(\frac{d y}{d x}\) = 0, (y ≠ 0)
Solution.
Given, y = \(\sqrt{a^{2}-x^{2}}\)
Differentiating both sides of this equation w.r.t. x, we get

Hence, the given function is the solution of the corresponding differential equation.

Direction (11 – 12) :
Choose the correct answer.

Question 11.
The number of arbitrary constants in the general solution of a differential equation of fourth order is
(A) Zero
(B) 2
(C) 3
(D) 4
Solution.
We know that the number of constants in the general solution of a differential equation of order n is equal to its order. Therefore, the number of constants in the general equation of fourth order differential equation is four.
Hence, the correct answer is (D).

Question 12.
The number of arbitrary constants in the particular solution of a differential equation of third order is
(A) 3
(B) 2
(C) 1
(D) zero
Solution.
In a particular solution of a differential equation, there are no arbitrary constants.
Hence, the correct answer is (D).