PSEB 12th Class Maths Solutions Chapter 9 Differential Equations Ex 9.3

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter Differential Equations Ex 9.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.3

Direction (1 – 5): In each question form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.

Question 1.
\(\frac{x}{a}+\frac{y}{b}\) = 1
Solution.
Given, family is \(\frac{x}{a}+\frac{y}{b}\) = 1
Differentiating both sides w.r.t. x, we get
\(\frac{1}{a}+\frac{1}{b} \frac{d y}{d x}\) = 0

⇒ \(\frac{1}{a}+\frac{1}{b} y\) = 0
Again, differentiating both sides w.r.t. x, we get
0 + \(\frac{1}{4}\) y” = 0
⇒ \(\frac{4}{4}\) y” = 0
⇒ y” = 0
Hence, the required differential equation of the given curve is y” = 0.

Question 2.
y² = a(b² – x²)
Sol.
Given, family is y² = a(b2 —x2)
Differentiating both sides w.r.t. x, we get
2y \(\frac{d y}{d x}\) = a(- 2x)
2yy’ = – 2ax
yy’= – ax ……………(i)
Again, differentiating both sides w.r.t. x, we get
y’ . y’ + yy” = – a
= (y’)² + yy” = – a ……………(ii)
Dividing equation (ii) by equation (i), we get
\(\frac{\left(y^{\prime}\right)^{2}+y y^{\prime \prime}}{y y^{\prime}}=\frac{-a}{-a x}\)

⇒ xyy” + x (y’)² – yy” = 0
This is the required differential equation of the given curve.

Question 3.
y = ae^3x + be^{– 2x}
Solution.
Given, family is y = ae^3x + be^{– 2x} ………………(i)
Differentiating both sides w.r.t. x, we get
y’ = 3ae^3x – 2 be^{– 2x} ………….(ii)
Again, differentiating both sides w.r.t. x, we get
⇒ y” = 9ae^3x + 4 be^{– 2x} …………….(iii)
Multiplying equation (i) with equation (ii) and then adding it from equation (ii), we get
(2ae^3x + 2be^{– 2x}) + (3ae^3x – 2 be^{– 2x}) = 2y + y’
⇒ 5ae^3x = 2y + y’
⇒ ae^3x = \(\frac{2 y+y^{\prime}}{5}\)
Now, multiplying equation (i) with equation (iii) and subtracting equation (ii) for, it, we get
(3ae^3x + 3be^{– 2x}) – (3ae^3x – 2be^{– 2x}) = 3y – y’
⇒ 5be^{– 2x} = 3y – y’
⇒ be^{– 2x} = \(\frac{3 y-y^{\prime}}{5}\)
Substituting the values of ae^3x and be^{– 2x} in equation (iii), we get
y” = \(9 \cdot \frac{\left(2 y+y^{\prime}\right)}{5}+4 \frac{\left(3 y-y^{\prime}\right)}{5}\)

⇒ y” = \(\frac{18 y+9 y^{\prime}}{5}+\frac{12 y-4 y^{\prime}}{5}\)

⇒ y” = \(\frac{30 y+5 y^{\prime}}{5}\)

⇒ y” = 6y + y’
⇒ y” – y’ – 6y = 0
This is the required differential equation of the given curve.

Question 4.
y = e^2x (a + bx)
Solution.
Given, y = e^2x (a + bx) ………….(i)
Differentiating both sides w.r.t. x, we get
y’ = 2e^2x (a + bx) + e^2x . b
⇒ y’ = e^2x (2a + 2 bx + b) ……………(ii)
Multiplying equation (i) with equation (ii) and then subtracting it from equation (ii), we get
y’ – 2y = e^2x (2a + 2bx + b) – e^2xx (2a + 2bx)
⇒ y’ – 2 = be^2x ……………..(iii)
Differentiating both sides w.r.t. x, we get
y”k – 2y’ = 2be^2x …………..(iv)
Dividing equation (iv) by equation (iii), we get
\(\frac{y^{\prime \prime}-2 y^{\prime}}{y^{\prime}-2 y}\) = 2
⇒ y” – 2y’ = 2y’ – 4y
⇒ y” – 4y’ + 4y = 0
This is the required differential equation of the given curve.

Question 5.
y = e^x (a cos x + b sin x)
Solution.
Given, y = e^x (a cos x + b sin x) …………..(i)
Differentiating both sides w.r.t. x, we get
y’ = e^x (a cos x + b sin x) + e^x (- a sin x + b cos x)
=> y’ = e^x [(a + b) cos x – (a – b) sin x] ……………(ii)
Again, differentiating both sides w.r.t. x, We get
y” = e^x [(a + b) cos x) – (a – b) sin x] + e^x [- (a + b) sin x – (a – b) cos x]
y” = e^x (2 b cos x – 2a sin x)
⇒ y” = 2 e^x (b cos x – a sin x)
Adding equations (i) and (iii), we get
y + \(\frac{y^{\prime \prime}}{2}\) = e^x [(a + b) cos x – (a – b) sin x]
⇒ y + \(\frac{y^{\prime \prime}}{2}\) = y’
⇒ 2y + y” = 2y
⇒ y” – 2y’ + 2y = 0
This is the required differential equation of the given curve.

Question 6.
Form the differential equation of the family of circles touching the y-axis at the origin.
Solution.
The equation of the circle with centre (a, 0) and radius a, which touches y-axis at origin
(x – a)² + y² = a²
x² + y² = 2ax ………….(i)

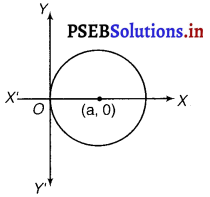
Differentiating equation w.r.t x
2x + 2y y’ = 2a
or x + y y’ = a
Put value of a in (i)
x² + y² = 2x (x + y y’)
= 2x² + 2xy y’
∴ Required differential equation is
2xy \(\frac{d y}{d x}\) + x² – y² = 0

Question 7.
Form the differential equation of the family of parabolas having vertex at origin and axis along positive y-axis.
Solution.

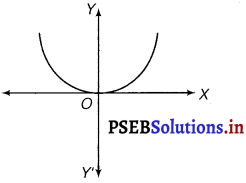
The equation of the parabola having the vertex at origin and the axis along the positive y-axis is
x² = 4ay ………..(i)
Differentiating equation (i) w.r.t. x, we get 2x = 4ay’ ………….(ii)
Dividing equation (ii) by equation (i), wex
\(\frac{2 x}{x^{2}}=\frac{4 a y^{\prime}}{4 a y}\)

⇒ \(\frac{2}{x}=\frac{y^{\prime}}{y}\)

⇒ xy’ = 2y
⇒ xy’ – 2y = 0
This is the required differential equation.

Question 8.
Form the differential equation of the family of ellipse having foci on y-is and centre at origin.
Solution.

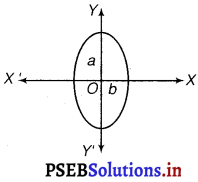
The equation of the family of ellipse having foci on they-axis and the centre at origin is as follows:
\(\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}\) = 1 …………….(i)
Differentiating equation (i) w.r.t. x, we get
\(\frac{2 x}{b^{2}}+\frac{2 y y^{\prime}}{a^{2}}\) = 0

⇒ \(\frac{x}{b^{2}}+\frac{y y^{\prime}}{a^{2}}\) = 0 …………..(ii)

Again, differentiating w.r.t. x, we get
\(\frac{1}{b^{2}}+\frac{y^{\prime} \cdot y^{\prime}+y \cdot y^{\prime \prime}}{a^{2}}\) = 0

⇒ \(\frac{1}{b^{2}}+\frac{1}{a^{2}}\left(y^{\prime 2}+y y^{\prime \prime}\right)\) = 0

⇒ \(\frac{1}{b^{2}}=-\frac{1}{a^{2}}\left(y^{2}+y y^{\prime \prime}\right)\)

x \(\left[-\frac{1}{a^{2}}\left(\left(y^{\prime}\right)^{2}+y y^{\prime \prime}\right)\right]+\frac{y y^{\prime}}{a^{2}}\) = 0

⇒ – x (y’)² – xyy” + yy’ = 0
⇒ xyy’ + x(y’)² – yy’ = 0
This is the required differential equation.

Question 9.
Form the differential equation of the family of hyperbolas having foci on x-axis and centre at origin.
Solution.

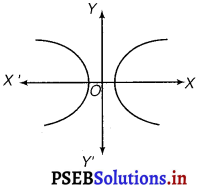
The equation of the family of hyperbolas with the centre at origin and foci along the x-axis is
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 ………………(i)

Differentiating both sides of equation (j) w.r.t. x, we get
\(\frac{2 x}{a^{2}}-\frac{2 y y^{\prime}}{b^{2}}\) = 0

\(\frac{x}{a^{2}}-\frac{y y^{\prime}}{b^{2}}\) = 0 …………….(ii)

Again, differentiating w.r.t. x, we get

\(\frac{1}{a^{2}}-\frac{y^{\prime} \cdot y^{\prime}+y y^{\prime \prime}}{b^{2}}\) = 0

\(\frac{1}{a^{2}}=\frac{1}{b^{2}}\left(\left(y^{\prime}\right)^{2}+y y^{\prime \prime}\right)\)
Substituting the value of in equation (ii), we get
\(\left.\frac{x}{b^{2}}\left(y^{\prime}\right)^{2}+y y^{\prime \prime}\right)-\frac{y y^{\prime}}{b^{2}}\) = 0

⇒ x (y’)² + xyy” – yy’ = 0
⇒ xyy” + x(y’)² – yy’ = 0
This is the required differential equation.

Question 10.
Form the differential equation of the family of circles having centre on y-axis and radius 3 units.
Solution.

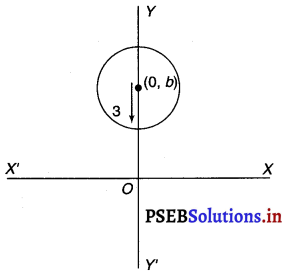
Let the centre of the circle on y-axis be (0, b).
The differential equation of the family of Circles with centre at (0, b) and radius 3 is as follows
x² + (y – b)² = 3²
⇒ x² + (y – b)² = 9 ……………(i)
Differentiating equation (i) w.r.t. x,
2x + 2(y – b) . y’ = 0
⇒ (y – b) . y’ = – x
⇒ y – b = \(\)
Substituting the value of (y – b) in equation (i), we get
x² + \(\left(\frac{-x}{y^{\prime}}\right)^{2}\) = 9

⇒ x² \(\left[1+\frac{1}{\left(y^{\prime}\right)^{2}}\right]\) = 9

⇒ x² ((y’)² + 1) = 9 (y’)x²

⇒ (x² – 9) (y’)² + x² = 0

This is the required differential equation.

Question 11.
Which of the following differential equations has y = c₁ e^x + c₂ e^x as the general solution?
(A) \(\frac{d^{2} y}{d x^{2}}\) + y = 0

(B) \(\frac{d^{2} y}{d x^{2}}\) – y = 0

(C) \(\frac{d^{2} y}{d x^{2}}\) + 1 = 0

(D) \(\frac{d^{2} y}{d x^{2}}\) – 1 = 0
Solution.
Given general solution is y = c₁ e^x + c₂ e^-x
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = c₁ e^x – c₂ e^-x
Again, differentiating w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = c₁ e^x + c₂ e^-x
⇒ \(\frac{d^{2} y}{d x^{2}}\) = y
⇒ \(\frac{d^{2} y}{d x^{2}}\) – y = 0
This is the required differential equation of the given equation of curve.
Hence, the correct answer is (B).

Question 12.
Which of the following differential equations has y = z as one of its particular solution?
(A) \(\frac{d^{2} y}{d x^{2}}-x^{2} \frac{d y}{d x}\) + xy = x

(B) \(\frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}\) + xy = x

(C) \(\frac{d^{2} y}{d x^{2}}-x^{2} \frac{d y}{d x}\) + xy = 0

(D) \(\frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}\) + xy = 0
Solution.
Given solution is y = x
Differentiating w.r.t. x, we get

\(\frac{d y}{d x}\) = 1 ……………….(i)

Again, differentiating w.r.t x, we get

\(\frac{d^{2} y}{d x^{2}\) = 0 ………………..(ii)

Now, on substituting the value of y, \(\frac{d^{2} y}{d x^{2}}\) and \(\frac{d y}{d x}\) from equation (i) and (ii) in each of the given alternatives, we find that only the differential
equation given in alternative C is correct.
\(\frac{d^{2} y}{d x^{2}}\) – x² \(\frac{d y}{d x}\) + xy = 0 – x² . 1 + x . x
= – x² + x² = 0
Hence, the correct answer is (C).