PSEB 12th Class Maths Solutions Chapter 9 Differential Equations Ex 9.5

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter Differential Equations Ex 9.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.5

Direction (1 – 10) :
In each question show that the given differential equation is homogeneous and solve each equation.

Question 1.
(x² + xy) dy = (x² + y²) dx
Solution.
The given differential equation, (x² + xy) dy = (x² + y²) dx can be written as

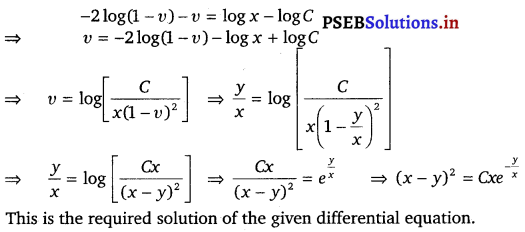
Question 2.
y’ = \(\frac{x+y}{x}\)
Solution.
The given differential equation is y’ = \(\frac{x+y}{x}\)
⇒ \(\frac{d y}{d x}=\frac{x+y}{x}\) ……………..(i)

Let F(x, y) = \(\frac{x+y}{x}\)

Now, F(λx, λy)= \(\frac{\lambda x+\lambda y}{\lambda x}=\frac{x+y}{x}\) = λ⁰ . F(x, y)
Thus, the given equation is a homogeneous equation.
Let y = vx
Differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}=v+x \frac{d v}{d x}\)
Substiting the values of y and \(\frac{d y}{d x}\) in equation (i), we get
v + \(x \frac{d v}{d x}=\frac{x+v x}{x}\)
⇒ v + x \(\frac{d v}{d x}\) = 1 + v
x \(\frac{d v}{d x}\) = 1
⇒ dv = \(\frac{d x}{x}\)
Integrating both sides, we get
v = log x + C
⇒ \(\frac{y}{x}\) = log x + C
⇒ y = x log x + Cx
This is the required solution of the given differential equation.

Question 3.
(x – y) dy – (x + y) dx = 0
Solution.
The given differential equation is (x – y) dy – (x + y) dx = 0
⇒ \(\frac{d y}{d x}=\frac{x+y}{x-y}\)

Let F(x, y) = \(\frac{x+y}{x-y}\)

This is the required solution of the given differential equation.

Question 4.
(x² – y²) dx + 2xy dy = 0
Sol.
The given differential equation is (x² – y²) dx + 2xy dy = 0

Therefore, the given differential equation is a homogeneous equation.
Let y = vx
Differentiating both sides w.r.t. x, we get
⇒ \(\frac{d}{d x}\) (y) = \(\frac{d}{d x}\) (vx)

⇒ \(\frac{d y}{d x}\) = v + x \(\frac{d v}{d x}\)

Substituting the values of y and \(\frac{d y}{d x}\) in equation (i), we get

Question 5.
x² \(\frac{d y}{d x}\) = x² – 2y² + xy
Solution.
The given differential equation is
x² \(\frac{d y}{d x}\) = x² – 2y² + xy ………………(i)

Question 6.
x dy – y dx = \(\sqrt{x^{2}+y^{2}}\) dx
Solution.
Given, x dy – y dx = \(\sqrt{x^{2}+y^{2}}\) dx
x dy = [y + \(\sqrt{x^{2}+y^{2}}\)] dx

Question 7.
\(\left\{x \cos \left(\frac{y}{x}\right)+y \sin \left(\frac{y}{x}\right)\right\} y d x=\left\{y \sin \left(\frac{y}{x}\right)-x \cos \left(\frac{y}{x}\right)\right\} x d y\)
Solution.
The given differential equation is

Therefore, the given differential equation is a homogeneous equation.
Let y = vx
Differentiating both sides w.r.t. x, we get

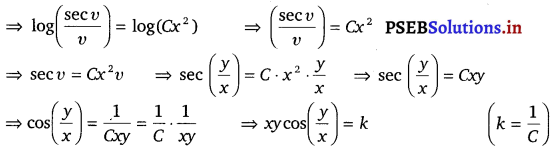
This is the required solution of the given differential equation.

Question 8.
x \(\frac{d y}{d x}\) – y + x sin \(\left(\frac{y}{x}\right)\) = 0
Solution.
Given, x \(\frac{d y}{d x}\) – y + x sin \(\left(\frac{y}{x}\right)\) = 0

Question 9.
y dx + x log \(\left(\frac{y}{x}\right)\) dy – 2x dy = 0
Solution.
Given, y dx + x log \(\left(\frac{y}{x}\right)\) dy – 2x dy = 0

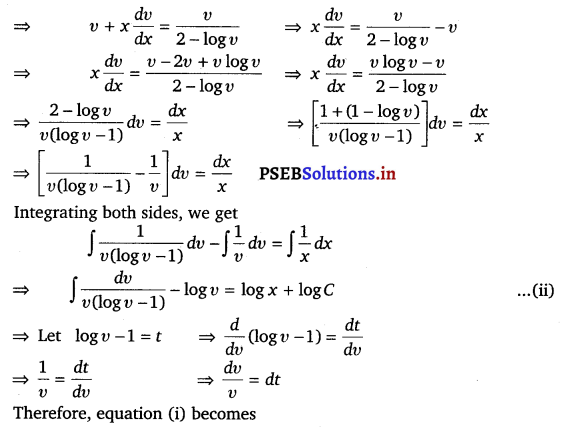
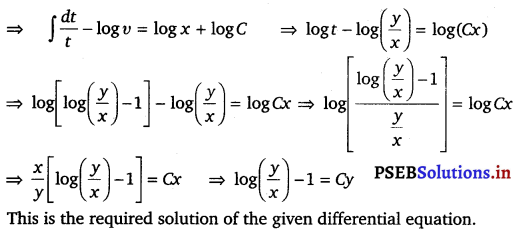
Question 10.
\(\left(1+e^{\frac{x}{y}}\right) d x+e^{\frac{x}{y}}\left(1-\frac{x}{y}\right) d y\) = 0
Solution.
Given, \(\left(1+e^{\frac{x}{y}}\right) d x+e^{\frac{x}{y}}\left(1-\frac{x}{y}\right) d y\) = 0

Therefore, the given differential equation is a homogeneous equation.
Let x = vy
Differentiating both sides w.r.t. x, we get
⇒ \(\frac{d}{d y}\) (x) = \(\frac{d}{d y}\) (vy)

⇒ \(\frac{d x}{d y}\) = v + y \(\frac{d v}{d y}\)
Substituting the values of x and latex]\frac{d x}{d y}[/latex] in equation (i), we get

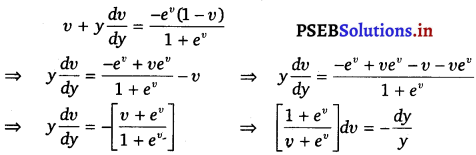
Integrating both sides w.r.t. x, we get

⇒ log (v + e^v) = – log y + log C = log \(\left(\frac{C}{y}\right)\)

⇒ \(\left[\frac{x}{y}+e^{\frac{x}{y}}\right]=\frac{C}{y}\)

⇒ x + y \(e^{\frac{x}{y}}\) = C
This is the required solution of the given differential equation.

Direction (11 – 15):
For each of the differential equation, find the particular solution satisfying the given condition.

Question 11.
(x + y) dy + (x – y) dy = 0; y = 1 when x = 1
Solution.
Given, (x + y) dy + (x – y)dx = O

Integrating both sides, we get
\(\frac{1}{2}\) log(1 + v²) + tan^{– 1} u = – log x + k
⇒ log (1 + v²) + 2 tan^{– 1} y = – 2 log x + 2k
⇒ log [(1 + v²) . x²] + 2 tan^{– 1} v = 2k
⇒ log [(1 + \(\frac{y^{2}}{x^{2}}\)) . x²] + 2 tan^{– 1} \(\frac{y}{x}\) = 2k
⇒ log (x² + y²) + 2 tan^{– 1} \(\frac{y}{x}\) = 2k
Now, y = 1 at x = 1
⇒ log 2 + 2 tan^{– 1}1 = 2k
⇒ log 2 + 2 × \(\frac{\pi}{4}\) = 2k
⇒ \(\frac{\pi}{2}\) + log 2 = 2k
Substituting the value of 2k in equation (ii), we get
log (x² + y²) + 2 tan^{– 1} (\(\frac{y}{x}\)) + log 2
This is the required solution of the given differential equation.

Question 12.
x² dy + (xy + y²)dx = 0; y = 1 when x = 1
Solution.
Given, x² dy + (xy + y²)dx = 0

Substituting C² = \(\frac{1}{3}\) in equation (ii), we get

\(\frac{x^{2} y}{y+2 x}=\frac{1}{3}\)

⇒ y + 2x = 3x²y
This is the required solution of the given differential equation.

Question 13.
\(\left[x \sin ^{2}\left(\frac{y}{x}-y\right)\right]\) dx + x dy = 0; y = \(\frac{\pi}{4}\) when x = 1.
Solution.
Given, \(\left[x \sin ^{2}\left(\frac{y}{x}-y\right)\right]\) dx + x dy = 0

When x = 1, then y = \(\frac{\pi}{4}\), therefore
log (1) – cot \(\frac{\pi}{4}\) = C
⇒ 0 – 1 = C
⇒ C = – 1
Putting the value of C in equation (i), we get
log x – cot \(\frac{y}{x}\) = – 1
log |x| – cot \(\frac{y}{x}\) = – log e
cot (\(\frac{y}{x}\)) = log |ex|
This is the required solution of the given differential euqation.

Question 14.
\(\frac{d y}{d x}\) – \(\frac{y}{x}\) + cosec (\(\frac{y}{x}\)) = 0; y = 0 when x = 1
Solution.
Given, \(\frac{d y}{d x}\) – \(\frac{y}{x}\) + cosec (\(\frac{y}{x}\)) = 0 …………..(i)
Which is homogeneous
Let y = vx
Differentiating both sides w.r.t. x,we get

When x = 1 then y = 0 therefore
log |1| – cos 0 = C
⇒ o – 1 = C,
⇒ c = – 1
Putting the value of C in equation (iii), we get
⇒ log |x| – cos (\(\frac{y}{x}\)) = – 1
⇒ log |x| + 1 = cos \(\frac{y}{x}\)
⇒ log |x| + log e = cos (\(\frac{y}{x}\))
⇒ log |ex| = cos (\(\frac{y}{x}\))
This is the required solution of the given differential equation.

Question 15.
2xy + y² – 2x² \(\frac{d y}{d x}\) = 0; y = 2 when x = 1.
Solution.
Given, 2xy + y² – 2x² \(\frac{d y}{d x}\) = 0

When x = 1 then y = 2
⇒ – 1 = log (1) + C
⇒ C = – 1
Substituting C = – 1 in equation (ii), we get
– \(\frac{2 x}{y}\) = log |x| – 1

\(\frac{2 x}{y}\) = 1 – log |x|

y = \(\frac{2 x}{1-\log |x|}\), (x ≠ 0, x ≠ e)
This is the required solution of the given differential equation.

Questio 16.
A homogeneous differential equation of the form \(\frac{d y}{d x}\) = h (\(\frac{x}{y}\)) can be solved by making the substitution
(A) y = vx
(B) v = yx
(C) x = vy
(D) x = v
Solution.
For solving the homogeneous equation of the form \(\frac{d y}{d x}\) = h (\(\frac{x}{y}\)), we need to make the substitution as x = vy.
Hence, the correct answer is (C).

Question 17.
Which of the following is a homogeneous differential equation?
(A) (4x + 6y + 5) dy – (3y + 2x + 4) dx = 0
(B) (xy) dx – (x³ + y³ )dy = 0
(C) (x² + 2y²) dx + 2xy dy = 0
(D) y² dx + (x² – xy – y²) dy = 0
Solution.
Function F(x, y) is said to be the homogeneous function of degree n, if
F(λx, λy) = λⁿ F(x, y) for any non-zero constant (λ).
Consider the equation given in alternative D.
y² dx + (x² – xy – y²) dy = 0

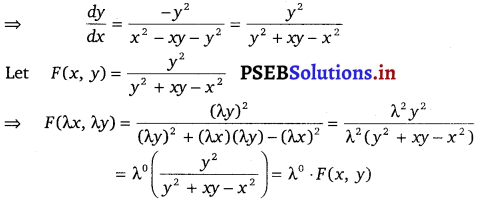
Hence, the differential equation given in alternative D is a homogenous equation.