PSEB 12th Class Maths Solutions Chapter 9 Differential Equations Ex 9.6

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter Differential Equations Ex 9.6 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.6

Direction (1 – 12): For each of the given differential equation, find the general solution.

Question 1.
\(\frac{d y}{d x}\) + 2y = sin x
Solution.
The given differential equation is \(\frac{d y}{d x}\) + 2y = sin x
This is in the form of \(\frac{d y}{d x}\) + Py = Q (where P = 2 and Q = sin x).
Now, I.F = e^{∫ P dx} = e^{∫ 2 dx} = e^2x.
The solution of the given differential equation is given by the relation,
y (I.F.) = ∫ (Q × I.F.) dx + C
⇒ ye^2x = ∫ sin x. e^2x dx + C …………….(i)
Let I = ∫ sin x. e^2x dx
⇒ I = sin x . ∫ e^2x dx – ∫ (\(\frac{d}{d x}\) (sin x) . ∫ e^2x dx) dx

Question 2.
\(\frac{d y}{d x}\) + 3y = e^{– 2x}
Solution.
The given differential equation is
\(\frac{d y}{d x}\) + 3y= e^{– 2x}
This is in the form of \(\frac{d y}{d x}\) + Py = Q (where P = 3 and Q = e^{– 2x})
Now, I.F.= e^{∫ P dx} = e^{∫ 3 dx} = e^3x
The solution of the given differential equation is given by the relation,
y (I.F.) = ∫ (Q × I.F.) dx + C
⇒ y e^3x = ∫ (e^{– 2x} × e^3x) + C
⇒ y e^3x = ∫e^x dx + C
⇒ y e^3x = e^x + C
⇒ ye^3x = e^{– 2x} + Ce^{– 3x}
This is the required general solution of the given differential equation.

Question 3.
\(\frac{d y}{d x}\) + \(\frac{y}{x}\) = x²
Solution.
The given differential equation is
\(\frac{d y}{d x}\) + \(\frac{y}{x}\) = x²
This is in the form of \(\frac{d y}{d x}\) + Py = Q (where P = \(\frac{1}{x}\) and Q = x²)
Now, I.F. = e^{∫ P dx}
= e^{∫ \(\frac{1}{x}\) dx}
= e^{log x} = x
The solution of the given differential equation is given by the relation
y (I.F.) = ∫ (Q × I.F.) dx + C
y(x) = ∫ (x² . x) dx + C
xy = ∫ x³ dx + C
⇒ xy = \(\frac{x^{4}}{4}\) + C
This is the required general solution of the given differential equation.

Question 4.
\(\frac{d y}{d x}\) + (sec x) y = tan x 0 ≤ x < 2
Solution.
The given differential equation is
\(\frac{d y}{d x}\) + (sec x) y = tan x
This is in the form of \(\frac{d y}{d x}\) + Py = Q (where P = sec x and Q = tan x)
Now, I.F = e^{∫ P dx}
= e^{∫ sec x}
= e^{log (sec x + tan x)}
= sec x + tan x
The general solution of the given differential equation is given by the relation
y (I.F.) = ∫ (Q × I.F.) dx + C
⇒ y (sec x + tan x) = ∫ tan x (sec x + tan x) dx + C
⇒ y (sec x + tan x) = ∫ sec x tan x dx + ∫ tan² x dx + C
⇒ y (sec x + tan x) = sec x + ∫ (sec² x – 1) dx + C
⇒ y (sec x + tan x) = sec x + tan x – x + C

Question 5.
cos² x \(\frac{d v}{d x}\) + y = tan x (0 ≤ x < \(\frac{\pi}{2}\))
Solution.
Given, cos² x \(\frac{d y}{d x}\) + y = tan x
On dividing by cos² x on both sides, we get
\(\frac{d y}{d x}+\frac{1}{\cos ^{2} x} y=\frac{\tan x}{\cos ^{2} x}\)
The equation is of the form \(\frac{d y}{d x}\) + Py = Q
(where P = \(\frac{1}{\cos ^{2} x}\) = sec² x, Q = \(\frac{\tan x}{\cos ^{2} x}\))
∴ I.F. = e^{∫ P dx}
= e^{∫ sec2 x}
= e^{tan x}
The general solution of the given differential equation is given by
y (I.F.) = ∫ (Q × I.F.) dx + C
i.e., y × e^{tan x} = ∫ \(\frac{\tan x}{\cos ^{2} x}\) e^{tan x} dx + C
= ∫ tan x . e sec² x + c
Put tan x = t, sec² x dx = dt
∴ ye^{tan x} = ∫ t e^t dt + C
Integrating by parts taking t as a first function.
= ye^{tan x} = te^t – ∫ 1 . e^t dt + C
= te^t – e^t + C
= tan x e^{tan x} – e^{tan x} + C (Putting t = tan x)
or y = tan x – 1 + Ce^{– tan x}

Question 6.
x \(\frac{d y}{d x}\) + 2y = x² log x
Solution.
The given differential equation is x \(\frac{d y}{d x}\) + 2y = x² log x
\(\frac{d y}{d x}\) + \(\frac{2}{dx}\) y = x log x
This equation is in the form of a linear differential equation as
\(\frac{d y}{d x}\) + Py = Q (where P = \(\frac{2}{x}\) and Q = x log X)
Now, I.F. = e^{∫ P dx}
= e^{∫ \(\frac{2}{x}\) dx}
= e^{2 log x}
= e^{log x2}
= x²
The general solution of the given differential equation is given by the relation,
y (I.F.) = ∫ (Q × I.F.) dx + C
y . x² = ∫ (x log x . x²) dx + C
x² y = ∫ (x³ log x) dx + C

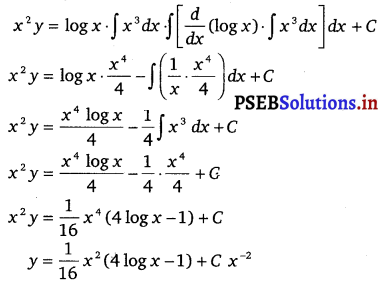
Question 7.
x log x \(\frac{d y}{d x}\) + y = log x
Solution.
The given differential equation is x log x \(\frac{d y}{d x}\) + y = \(\frac{2}{x}\) log x

⇒ \(\frac{d y}{d x}+\frac{y}{x \log x}=\frac{2}{x^{2}}\)
This equation is the form of a linear differential equation as

\(\frac{d y}{d x}\) + Py = Q, (where P = \(\frac{1}{x \log x}\) and Q = \(\frac{2}{x^{2}}\))

Now, I.F. = e^{∫ P dx}
= e^{∫ \(\frac{1}{x \log x}\) dx}
= e^{log (log x)} = log x

The general solution of the given differential equation is given by the relation,
y(I.F.) = ∫ (Q × I.F.) dx + C

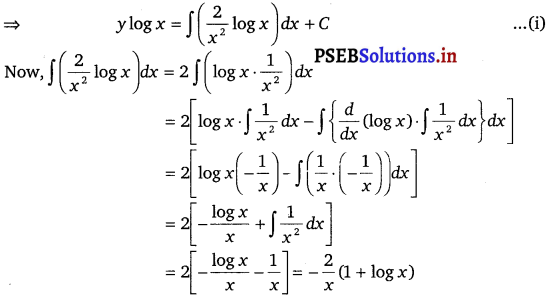
Substiting the value of ∫ (\(\frac{2}{x^{2}}\) log x) in equation (i), we get
y log x = – \(\frac{2}{x}\) (1 + log x) + C
This is the required general solution of the given differential equation.

Question 8.
(1 + x²) dy + 2xy dx = cot x dx (x ≠ 0)
Solution.
Given, (1 + x²) dy + 2xy dx = cot x dx

⇒ \(\frac{d y}{d x}+\frac{2 x y}{1+x^{2}}=\frac{\cot x}{1+x^{2}}\)

This equation is a linear differential equation of the form
\(\frac{d y}{d x}\) + Py = Q (where P = \(\frac{2 x}{1+x^{2}}\) and Q = \(\frac{\cot x}{1+x^{2}}\))

Now, I.F. = e^{∫ P dx}
= e^{\(\frac{2 x}{1+x^{2}}\) dx}
= e^{log (1 + x2)}
= 1 + x²
The general solution of the given differential equation is given by the relation,
y × I.F. = ∫ (Q × l.F.) dx
⇒ y (1 + x²) = ∫ [\(\frac{\cot x}{1+x^{2}}\) (1 + x²)] dx + C
⇒ y (1 + x²) = ∫ cot x dx + C
⇒ y (1 + x²) = log |sin x| + C

Question 9.
x \(\frac{d y}{d x}\) + y – x + xy cot x = 0,(x ≠ 0)
Solution.
Given, x \(\frac{d y}{d x}\) + y – x + xy cot x = 0
⇒ x \(\frac{d y}{d x}\) + y (1 + x cot x) = x
⇒ \(\frac{d y}{d x}\) + (\(\frac{1}{x}\) + cot x) y = 1
This is a linear differential equation of the form
\(\frac{d y}{d x}\) + Py = Q
(where P = \(\frac{1}{x}\) + cot x and Q = 1)
Now, I.F. = e^{∫ P dx}
= e^{(\(\frac{1}{x}\) + cot x) dx}
= e^{log x + log (sin x)}
= e^{log (x sin x)}
= x sin x
The general solution of the given differential equation is given by the relation,
y × I.F. = ∫ (Q × I.F.) dx
⇒ y (x sin x) = ∫ (1 × x sin x) dx + C
⇒ y (x sin x) = ∫ (x sin x) dx + C
⇒ y (x sin x) = x ∫ sin x dx – ∫ [\(\frac{d}{d x}\) (x) . ∫ sin x dx] + C
⇒ y (x sin x) = x(- cos x) – ∫ 1 .(- cos x) dx + C
⇒ y (x sin x) = – x cos x + sin x + C

⇒ y = \(\frac{-x \cos x}{x \sin x}+\frac{\sin x}{x \sin x}+\frac{C}{x \sin x}\)

y = – cot x + \(\frac{1}{x}+\frac{C}{x \sin x}\)

Question 10.
(x + y) \(\frac{d y}{d x}\) = 1
Solution.
Given, (x + y) \(\frac{d y}{d x}\) = 1
⇒ \(\frac{d y}{d x}=\frac{1}{x+y}\)

⇒ \(\frac{d y}{d x}\) = x + y

⇒ \(\frac{d y}{d x}\) – x = y
This is a linear differential equation of the form
\(\frac{d x}{d y}\) + P₁x = Q₁ (where P₁ = – 1 and Q₁ = y)
Now, I.F. = e^{∫ P dx}
= e^{∫ – dy}
= e^{– y}
The general solution of the given differentia1 equation is given by the relation,
x (I.F.) = ∫ (Q × I.F.) dy + C
⇒ xe^{– y} = ∫ (y . e^{– y}) dy + C
⇒ xe^{– y} = y ∫ e^{– y} dy – ∫ [\(\frac{d}{d y}\) (y) ∫ e^{– y} dy] dy + C
⇒ xe^{– y} = y(- e^{– y}) – ∫ (- e^{– y}) dy + C
⇒ xe^{– y} = – ye^{– y} + ∫ e^{– y} dy + C
⇒ xe^{– y} = – ye^{– y} – e^{– y} + C
⇒ x = – y – 1 + C e^y
⇒ x + y + 1 = Ce^y

Question 11.
y dx + (x – y²) dy = 0
Solution.
Given y dx + (x – y²) dy = 0
⇒ y dx = (y² – x) dy
⇒ \(\frac{d x}{d y}\) = \(\frac{y^{2}-x}{y}=y-\frac{x}{y}\)

⇒ \(\frac{d x}{d y}+\frac{x}{y}\) = y
This is a linear differential equation of the form
\(\frac{d x}{d y}\) + P₁x = Q₁ (where P₁ = \(\frac{1}{y}\) and Q₁ = y)
Now, I.F. = e^{∫ P₁ x dx}
= e^{∫ \(\frac{1}{y}\) dy}
= e^{log y} = y
The general solution of the given differential equation is given by the relation,
⇒ x × I.F.= ∫ (Q₁ × I.F.) dy + C
⇒ xy = ∫ (y.y) dy + C
⇒ xy = ∫ y² dx + C
⇒ xy = \(\frac{y^{3}}{3}\) + C
⇒ x = \(\frac{y^{2}}{3}+\frac{C}{y}\).

Question 12.
(x + 3y²) \(\frac{d y}{d x}\) = y (y > 0)
Solution.
Given, (x + 3y²) \(\frac{d y}{d x}\) = y

⇒ \(\frac{d y}{d x}=\frac{y}{x+3 y^{2}}\)

⇒ \(\frac{d x}{d y}=\frac{x+3 y^{2}}{y}=\frac{x}{y}+3 y\)

⇒ \(\frac{d x}{d y}-\frac{x}{y}\) = 3y
This is a linear differential equation of the form
\(\frac{d x}{d y}\) + P₁ x = Q₁
(where P₁ = – \(\frac{1}{y}\) and Q₁ = 3y)
Now, I.F. = e^{∫ P₁ dx}
= e^{– ∫ \(\frac{d y}{y}\)}
= e^{– log y}
= e^{log (\(\frac{1}{y}\))}
= \(\frac{1}{y}\)
The general solution of the given differential equation is given by the relation.
x × I.F.= ∫ (Q₁ × I.F.) dy + C
⇒ x × \(\frac{1}{y}\) = ∫ (3y × \(\frac{1}{y}\)) dy + C
⇒ \(\frac{x}{y}\) = 3y + C
⇒ x = 3y² + Cy.

Direction (13 – 15): For each of the differential equation, find a particular solution satisfying the given condition.

Question 13.
\(\frac{d y}{d x}\) + 2y tan x = sin x; y = 0 when x = \(\frac{\pi}{3}\)
Solution.
The given differential equation is \(\frac{d y}{d x}\) + 2y tan x = sin x
This is a linear differential equation of the form
\(\frac{d y}{d x}\) + Py = Q (where P = 2 tan x and Q = sin x)
Now, I.F. = e^{∫ P dx}
= e^{∫ 2 tan x dx}
= e^{2 log |sec x|}
= e^{log (sec2 x)}
= sec² x
The general solution of the given differential equation is given by the relation,
x (I.F.) = ∫ (Q × I.F.) dx + C
⇒ y (sec² x) = ∫ (sin x . sec² x) dx + C
⇒ y sec² x = ∫ (sec x . tan x) dx + C
⇒ y sec² x = sec x + C ……………(i)
Now, y = 0 at x = \(\frac{\pi}{3}\)
Therefore,
0 × sec² \(\frac{\pi}{3}\) = sec\(\frac{\pi}{3}\) + C
⇒ 0 = 2 + C
⇒ C = – 2
Substituting C = – 2 in equation (i), we get
y sec² x = sec x – 2
y = cos x – 2 cos² x
Hence, the required solution of the given differential equation is y = cos x – 2 cos² x.

Question 14.
(1 + x²) \(\frac{d y}{d x}\) + 2xy = \(\frac{1}{1+x^{2}}\); y = 0 when x = 1
Solution.
Given, (1 + x²) \(\frac{d y}{d x}\) + 2xy = \(\frac{1}{1+x^{2}}\)

⇒ \(\frac{d y}{d x}+\frac{2 x y}{1+x^{2}}=\frac{1}{\left(1+x^{2}\right)^{2}}\)
This is a linear differential equation of the form
\(\frac{d y}{d x}\) + Py = Q (where P = \(\frac{2 x}{1+x^{2}}\) and Q = \(\frac{1}{\left(1+x^{2}\right)^{2}}\))
Now, I.F. = e^{∫ P dx}
= e^{\(\int \frac{2 x d x}{1+x^{2}}\)}
= e^{log (1 + x2)} = 1 + x²
The general solution of the given differential equation is given by the relation,
x (I.F.) = ∫ (Q × I.F.)dx + C
⇒ y(1 + x²) = \(\left[\frac{1}{\left(1+x^{2}\right)^{2}} \cdot\left(1+x^{2}\right)\right]\) dx + C
⇒ y (1 + x²) = ∫ \(\frac{1}{1+x^{2}}\) dx + C
y (1 + x²) = tan^-1 x + C ……………..(i)
Now, y = 0 at x = 1
Therefore, 0 = tan^-1 1 + C
⇒ C = – \(\frac{\pi}{4}\)
Substituting C = – \(\frac{\pi}{4}\) in equation (i), we get
y (1 + x²) = tan^-1 x – \(\frac{\pi}{4}\)
This is the required general solution of the given differential equation.

Question 15.
\(\frac{d y}{d x}\) – 3y cot x = sin 2x; y = 2 when x = \(\frac{\pi}{2}\).
Solution.
The given differential equation is \(\frac{d y}{d x}\) – 3y cot x = sin 2x
This is a linear differential equation of the form
\(\frac{d y}{d x}\) + Py = Q (where P = – 3 cot x and Q = sin 2x)
Now, I.F. = e^{∫ P dx}
= e^{– 3 ∫ cot x dx}
= e^{– 3 log |sin x|}
= e^{log \(\left|\frac{1}{\sin ^{3} x}\right|\)}

= \(\frac{1}{\sin ^{3} x}\)

The general solution of the given differential equation is given by the relation,
y(I.F.) = ∫ (Q × I.F.) dx + C
⇒ \(y \cdot \frac{1}{\sin ^{3} x}=\int\left[\sin 2 x \cdot \frac{1}{\sin ^{3} x}\right] d x+C\)

⇒ y cosec³ x = 2 ∫ (cot x cosec x) dx + C
⇒ y cosec³ x = 2 cosec x + c
⇒ y = \(-\frac{2}{\operatorname{cosec}^{2} x}+\frac{3}{\operatorname{cosec}^{3} x}\)
y = – 2 sin² x + C sin³ x ………..(i)
Now, y = 2 at x = \(\frac{\pi}{2}\)
Therefore, we get
2 = – 2 + C
⇒ C = 4
Substituting C = 4 in equation (i), we get
y = – 2 sin² x + 4 sin³ x
y = 4 sin³ x – 2 sin² x
This is the required particular solution of the given differential equation.

Question 16.
Find the equation of a curve passing through the origin given that the slope of the tangent to the curve at any point (x, y) is equal to the sum of the coordinates of the point.
Solution.
Let F(x, y) be the curve passing through the origin.
At point (x, y), the slope of the curve will be \(\frac{d y}{d x}\).
According to the given information,
\(\frac{d y}{d x}\) = x + y
⇒ \(\frac{d y}{d x}\) – y = x
This is a linear differential equation of the form
\(\frac{d y}{d x}\) + Py = Q (where P = – 1 and Q = x)
Now, I.F. = e^{∫ P dx}
= e^{∫ (- 1)} dx
= e^{– x}
The general solution of the given differential equation is given by the relation,
y(I.F.) = ∫ (Q × I.F.) dx + C
ye^{– x} = ∫ xe^{– x} dx + C ……………(i)
Now, ∫ xe^{– x} dx = x ∫ e^{– x} dx – ∫ \(\left[\frac{d}{d x}(x) \cdot \int e^{-x} d x\right]\) dx
= – xe^{– x} – ∫ – e^{– x} dx
= – xe^{– x} + (- e^{– x})
= – e^{– x} (x + 1)
Substituting in equation (i), we get
ye^{– x} = – e^{– x} (x + 1) + C
⇒ y = – (x + 1) + Ce^x
⇒ x + y + 1 = Ce^x ………….(ii)
The curve passes through the origin.
Therefore, equation (ii) becomes
1 = C
Substituting C = 1 in equation (ii), we get
⇒ x + y + 1 = e^x
Hence, the required equation of curve passing through the origin is x + y+ 1 = e^x.

Question 17.
Find the equation of a curve passing through the point (0, 2) given that the sum of the coordiDntes of any point on the curve exceeds the magnitude of the slope of the tangent to the curve at that point by 5.
Solution.
According to question, we have x + y = \(\frac{d y}{d x}\) + 5
or \(\frac{d y}{d x}\) + (- 1) y = x – 5
It is a linear differential equation of the form \(\frac{d y}{d x}\) + Py = Q
∴ P = – 1 andQ = x – 5 and
I.F. = e^{∫ P dx}
l.F. = e^{– x}
The general equation of the curve is given by
y. I.F = ∫ Q × I.F dx + C
⇒ y . e^{– x} = ∫ (x – 5) e^{– x} dx + C
⇒ y . e^{– x} = (x – 5) ∫ e^{– x} dx – ∫ [\(\frac{d}{d x}\) (x – 5) . ∫ e^{– x} dx] dx + C
⇒ y . e^{– x} = (x – 5) (- e^{– x}) – ∫ (- e^{– x}) dx + C
⇒ y . e^{– x} = (5 – x) e^{– x} – e^{– x} + C ……………(ii)
The curve passes through the point (0, 2), therefore
2 e^{– 0} = (5 – 0) e^{– 0} – e⁰ + C
⇒ 2 = 5 – 1 + C
⇒ C = 2 – 4 = – 2
On putting the value of C in equation (ii), we get
e^{– x} y = (5 – x) e^{– x} – e^{– x} – 2
⇒ y = 4 – x – 2e^{– x}
which is the required equation of the curve in reference.

Question 18.
The integrating factor of the differential equation x \(\frac{d y}{d x}\) – y = 2x²
(A) e^{– x}
(B) e^{– y}
(C) \(\frac{1}{x}\)
(D) x
Solution.
The given differential equation is x \(\frac{d y}{d x}\) – y = 2x²
⇒ \(\frac{d y}{d x}\) – \(\frac{y}{x}\) = 2x
This is a linear differential equation of the form
\(\frac{d y}{d x}\) + Py = Q
(where P = – \(\frac{1}{x}\) and Q = 2x)
The integrating factor (1.F.) is given by the relation e^{∫ P dx}
∴ I.F. = e^{∫ \(\frac{1}{x}\) dx}
= e^{∫ – log x}
= e^{log (x-1)}
= x^-1
= \(\frac{1}{x}\)
Hence, the correct answer is (C).

Question 19.
The integrating factor of the differential equation (1 – y²) \(\frac{d x}{d y}\) + yx = ay (- 1 < < 1) is
(A) \(\frac{1}{y^{2}-1}\)

(B) \(\frac{1}{\sqrt{y^{2}-1}}\)

(C) \(\frac{1}{1-y^{2}}\)

(D) \(\frac{1}{\sqrt{1-y^{2}}}\)
Solution.
The given differential equation is (1 – y²) \(\frac{d x}{d y}\) + yx = ay

⇒ \(\frac{d x}{d y}+\frac{y x}{1-y^{2}}=\frac{a y}{1-y^{2}}\)

This is a linear differential equation of the form
\(\frac{d x}{d y}\) + P₁ x = Q₁
(where P₁ = \(\frac{y}{1-y^{2}}\) and Q₁ = \(\frac{a y}{1-y^{2}}\))
The integrating factor (I.Fj is given by the relation e^{∫ P₁ dx}
∴ I.F.= e^{∫ P₁ dy}

= \(e^{\int \frac{y}{1-y^{2}} d y}=e^{-\frac{1}{2} \log \left(1-y^{2}\right)}=e^{\log \left[\frac{1}{\sqrt{1-y^{2}}}\right]}=\frac{1}{\sqrt{1-y^{2}}}\)
Hence, the correct answer is (D).