PSEB 12th Class Maths Solutions Chapter 9 Differential Equations Miscellaneous Exercise

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 9 Differential Equations Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 9 Differential Equations Miscellaneous Exercise

Question 1.
For each of the differential equations given below, indicate its order and degree (if defined).
(i) \(\frac{d^{2} y}{d x^{2}}+5 x\left(\frac{d y}{d x}\right)^{2}\) – 6y = log x

(ii) \(\left(\frac{d y}{d x}\right)^{3}-4\left(\frac{d y}{d x}\right)^{2}\) + 7y = sin x

(iii) \(\frac{d^{4} y}{d x^{4}}-\sin \left(\frac{d^{3} y}{d x^{3}}\right)\) = 0
Solution.
(i) The given differential equation is \(\frac{d^{2} y}{d x^{2}}+5 x\left(\frac{d y}{d x}\right)^{2}\) – 6y = log x

\(\frac{d^{2} y}{d x^{2}}+5 x\left(\frac{d y}{d x}\right)^{2}\) – 6y – log x = 0
The highest order derivative present in the differential equation is \(\frac{d^{2} y}{d x^{2}}\).
Thus, its order is 2.
The highest power raised to \(\frac{d^{2} y}{d x^{2}}\) is one.
Hence, its degree is 1.

(ii) The given differential equation is \(\) + 7y = sin x

\(\left(\frac{d y}{d x}\right)^{3}-4\left(\frac{d y}{d x}\right)^{2}\) + 7y – sin x = 0
The highest order derivative present in the differential equation is \(\frac{d y}{d x}\).
Thus, its order is 1.
The highest power raised to \(\frac{d y}{d x}\) is three.
Hence, its degree is 3.

(iii) The given differential equation is \(\frac{d^{4} y}{d x^{4}}-\sin \left(\frac{d^{3} y}{d x^{3}}\right)\) = o
The highest order denvative present in the differential equation is \(\frac{d^{4} y}{d x^{4}}\).
Thus, its order is 4.
However, the given differential equation is not a polynomial equation.
Hence, its degree is not defined.

Question 2.
For each of the questions given below, verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.
(i) y = ae^x + e^-x + x² : \(x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}\) – xy + x² – 2 = 0

(ii) y = e^x (a cos x + sin x) : \(\frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+2 y=0\)

(iii) y = x sin 3x : \(x \frac{d^{2} y}{d x^{2}}\) + 9y – 6 cos 3x = 0

(iv) x² = 2y² log y : (x² + y²) \(\frac{d y}{d x}\) – xy = 0
Solution.
(i) Given, y = ae^x + be^{– x} + x²
Differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}=a \frac{d}{d x}\left(e^{x}\right)+b \frac{d}{d x}\left(e^{-x}\right)+\frac{d}{d x}\left(x^{2}\right)\)

\(\frac{d y}{d x}\) = ae^x – be^{– x} + x²
Again, differentiating both sides w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = ae^x + be^{– x} + x²
Now, on substituting the values of \(\frac{d y}{d x}\) and \(\frac{d^{2} y}{d x^{2}}\) in the differential equation, we get
L.H.S. = x\(\frac{d^{2} y}{d x^{2}}\) + 2 \(\frac{d y}{d x}\) – xy + x² – 2
= x (ae^x + be^{– x} + 2) + 2 (ae^x – be^{– x} + 2x) – x (ae^x + be^{– x} + x²) + x² – 2

= (axe^x + bxe^{– x} + 2x) + (2ae^x – 2be^{– x} + 4x) – (axe^x + bxe^-x + x³) + x² – 2

= 2ae^x – 2be^-x + x² + 6x – 2 ≠ 0
= L.H.S. ≠ R.H.S.
Hence, the given function is not a solution of the corresponding differential equation.

(ii) Given, y = e^x (a cos x + b sin x)
= a e^x cos x + b e^x sin x
Differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}\) = a . \(\frac{d}{d x}\) (e^x cos x) + b . \(\frac{d}{d x}\) (e^x sin x)

⇒ \(\frac{d y}{d x}\) = a (e^x cos x – e^x sin x) + b . (e^x sin x + e^x cos x)

⇒ \(\frac{d y}{d x}\) = (a + b) e^x cos x + (b – a) e^x sin x
Again, differentiating both sides w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = (a + b) . \(\frac{d}{d x}\) . (e^x cos x) + (b – a) \(\frac{d}{d x}\) (e^x sin x)

\(\frac{d^{2} y}{d x^{2}}\) = (a + b) . [e^x cos x – e^x sin x + (b – a) e^x sin x + e^x cos x]

\(\frac{d^{2} y}{d x^{2}}\) = e^x [(a + b) (cos x – sin x) + (b – a) (sin x + cos x)]

\(\frac{d^{2} y}{d x^{2}}\) = e^x [a cos x – a sin x + b cos x – b sin x + b sin x + b cos x – a sin x – a cos x]

\(\frac{d^{2} y}{d x^{2}}\) = [2e^x (b cos x – a sin x)] d2 dy
Now, on substituting the values of \(\frac{d^{2} y}{d x^{2}}\) and \(\frac{d y}{d x}\) in the L.H.S. of the given differential equation, we get

\(\frac{d^{2} y}{d x^{2}}\) + 2 \(\frac{d y}{d x}\) + 2y = 2 e^x (b cos x – a sin x) – 2 e^x [(a + b) cos x + (b – a) sin x] + 2 e^x (a cos x + b sin x)
= e^x [(2b c0s x – 2a sin x) – (2a cos x + 2b cos x) – 2b sin x – 2a sin x) + (2a cos x + 2b sin x)]
= e^x [(2b – 2a – 2h + 2a) cos x] + e^x [(- 2a – 2b + 2a + 2b) sin x]
=0
Hence, the given function is a solution of the corresponding differential equation.

(iii) Given, y = x sin 3x
Differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (x sin 3x)
= sin 3x + x . cos 3x . 3
= \(\frac{d y}{d x}\) = sin 3x + 3x cos 3x
Again differentiating both sides w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac{d}{d x}\) (sin 3x) + 3 \(\frac{d}{d x}\) (x cos 3x)

\(\frac{d^{2} y}{d x^{2}}\) = 3 cos 3x + 3 [cos 3x + x (- sin3x). 3]

\(\frac{d^{2} y}{d x^{2}}\) = 6 cos 3x – 9 x sin 3x

Substituting the value of \(\frac{d^{2} y}{d x^{2}}\) in the L.H.S. of the given differential equation, we get

\(\frac{d^{2} y}{d x^{2}}\) + 9y – 6 cos 3x = (6 cos 3x – 9 x sin 3x) + 9x sin 3x – 6 cos 3x = 0
Hence, the given function is a solution of the corresponding differential equation.

(iv) Given, x² = 2y² log y
Differentiating both sides w.r.t. x, we get
2x = 2 . \(\frac{d}{d x}\)
= [y² log y]

⇒ x = [2y . log y . \(\frac{d y}{d x}\) + y² . \(\frac{1}{y}\) . \(\frac{d y}{d x}\)]

x = \(\frac{d y}{d x}\) (2y log y + y)

⇒ \(\frac{d y}{d x}\) = \(\frac{x}{y(1+2 \log y)}\)
Substituting the value of \(\frac{d y}{d x}\) in the L.H.S. of the given differential equation, we get

(x² + y²) \(\frac{d y}{d x}\) – xy = (2y² log y + y²) . \(\frac{x}{y(1+2 \log y)}\) – xy

= y² (1 + 2 log y) . \(\frac{x}{y(1+2 \log y)}\) – xy

= xy – xy = 0

Hence, the given function is a solution of the corresponding differential equation.

Question 3.
Form the differential equation representing the family of curves given by (x – a)² + 2y² = a², where a is an arbitrary constant.
Solution.
Given family of curves (x – a)² + 2y² = a²
⇒ x² + a² – 2ax + 2y² = a²
⇒ 2y² = 2ax – x²
Differentiating with respect w.r.t. x, we get
2y \(\frac{d y}{d x}\) = \(\frac{2 a-2 x}{2}\)

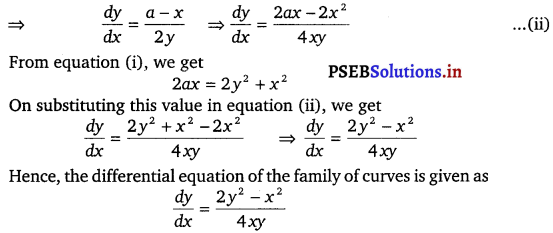
Question 4.
Prove that x² – y² = c (x² + y²)² is the general solution of differential equation (x³ – 3xy²)dx = (y² – 3x²y) dy, where c is a parameter.
Solution.
The differential equation is (x³ – 3xy²)dx = (y³ – 3x²y) dy
∴ \(\frac{d y}{d x}=\frac{x^{3}-3 x y^{2}}{y^{3}-3 x^{2} y}\) ……………(i)
This is a homogeneous equation.
Let y = vx
Differentiating w.r.t. x, we get

x² – y² = c (x² + y²)²
Hence, x² – y² = c (x² + y²)² is the solution of the differential equation.
(x³ – 3xy²)dx = (y³ – 3x²y) dy where c is a parameter.

Question 5.
Form the differential equation of the family of circles in the first quadrant which touch the coordinates axes.
Solution.
The equation of a circle in the first quadrant with centre (a, a) and radius
(a) which touches the coordinate axis is
(x – a)² + (y – a)² = a²

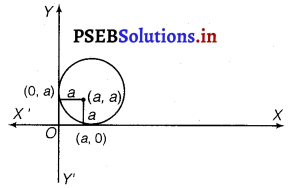
Differentiating eq (i) w.r.t x, we get
2 (x – a) + 2 (y – a) \(\frac{d y}{d x}\) = 0
⇒ (x – a) + (y – a) y’ = 0
⇒ x – a + yy’ – ay’ = 0
⇒ x + yy’ – a (1 – y’) = 0
⇒ a = \(\frac{x+y y^{\prime}}{1+y^{\prime}}\)
Substituting the value of a in equation (i), we get
\(\left[x-\left(\frac{x+y y^{\prime}}{1+y^{\prime}}\right)\right]^{2}+\left[y-\left(\frac{x+y y^{\prime}}{1+y^{\prime}}\right)\right]^{2}+\left(\frac{x+y y^{\prime}}{1+y^{\prime}}\right)^{2}\)

⇒ \(\left[\frac{(x-y) y^{\prime}}{\left(1+y^{\prime}\right)}\right]^{2}+\left[\frac{y-x}{1+y^{\prime}}\right]^{2}+\left[\frac{x+y y^{\prime}}{1+y^{\prime}}\right]^{2}\)

⇒ (x – y)² . y’² + (x – y) = (x +yy’)

⇒ (x – y)² [1 + (y’)²] = (x + yy’)²
Hence, the required differential equation of the family of circles is (x – y)² [1 + (y’)²] = (x + yy’)^2.

Question 6.
Find the general solution of the differential equation \(\frac{d y}{d x}+\sqrt{\frac{1-y^{2}}{1-x^{2}}}\) = 0
Solution.
Given, differential equation is \(\frac{d y}{d x}+\sqrt{\frac{1-y^{2}}{1-x^{2}}}\) = 0
⇒ \(\frac{d y}{d x}=-\frac{\sqrt{1-y^{2}}}{\sqrt{1-x^{2}}}\)

⇒ \(\frac{d y}{\sqrt{1-y^{2}}}=\frac{d x}{\sqrt{1-x^{2}}}\)
Integrating both sides, we get
sin^-1 y = – sin^-1 x + C
⇒ sin^-1 x + sin^-1 y = C.

Question 7.
Show that the general solution of the differential equation \(\frac{d y}{d x}+\frac{y^{2}+y+1}{x^{2}+x+1}\) is given by (x + y + 1) = A (1 – x – y – 2xy) where A is parameter.
Solution.

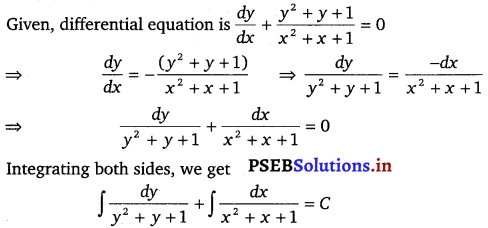
Hence, the given result is proved.

Question 8.
Find the equation of the curve passing through the point (o, \(\frac{\pi}{4}\)) whose differential equation is sin x cos y dx + cos x sin y dy = 0.
Solution.
The differential equation of the given curve is sin x cos y dx + cos x sin y dy = 0
⇒ \(\frac{\sin x \cos y d x+\cos x \sin y d y}{\cos x \cos y}=0\)

⇒ tan x dx + tan y dy = 0
Integrating both sides, we get
log (sec x) + log (sec y) = log C
log (sec x sec y) = log C
⇒ sec x . sec y = C
The curve passes through point (0, \(\frac{\pi}{4}\))
∴ 1 × √2 = C
⇒ C = √2
On substituting the value of C in equation (i), we get
sec x . sec y = √2
sec x . \(\frac{1}{cos y}\) = √2

⇒ cos y = \(\frac{\sec x}{\sqrt{2}}\)

Hence, the required equation of the curve is cos y = \(\frac{\sec x}{\sqrt{2}}\).

Question 9.
Find the particular solution of the differential equation (1 + e^2x) dy + (1 + y²) e^x dx = 0, given that y = 1 when x = 0.
Solution.
The differential equation is
(1 + e^2x) dy + (1 + y²) e^x dx = 0
On separating the variables, we get

\(\frac{d y}{1+y^{2}}+\frac{e^{x} d x}{1+e^{2 x}}\) = 0

Integrating both sides, we get
\(\int \frac{d y}{1+y^{2}}+\int \frac{e^{x}}{1+e^{2 x}} d x\) = C

Put e^x = t,
e^x dx = dt
∴ tan^-1 y + \(\int \frac{d t}{1+t^{2}}\) = C
tan^-1 y + tan^-1 t = C
i.e., tan^-1 y + tan^-1 e^x = C
Put y = 1, x = 0
∴ tan^-1 1 + tan^-1 1 = C or
2 tan^-1 1 = C
2 × \(\frac{\pi}{4}\) = C
∴ C = \(\frac{\pi}{2}\)
The particular solution of the given differential equation is
tan^-1 y + tan^-1 e^x = \(\frac{\pi}{2}\)

Question 10.
Solve the differential equation \(y e^{\frac{x}{y}} d x=\left(x e^{\frac{x}{y}}+y^{2}\right) d y\) (y ≠ 0)
Solution.
Given differential equation is \(y e^{\frac{x}{y}} d x=\left(x e^{\frac{x}{y}}+y^{2}\right) d y\)

From equation (î) and equation (ii), we get
\(\frac{d z}{d y}\) = 1
⇒ dz = dy
Integrating both sides, we get
z = y + C
⇒ e^{\(\frac{x}{y}\)} = y + C.

Question 11.
Find a particular solution of the differential equation (x – y) (dx + dy) = dx – dy, given that y = – 1, when x = 0.
(Hint: put x – y = t).
Solution.
Given differential equation is (x – y) (dx + dy) = dx – dy

Integrating both sides, we get
t + |log t| = 2x + C
⇒ (x – y) + log(x – y) = 2x + C
log |x – y| = x + y + C …………….(iii)
Now, y = – 1 at x = 0.
Therefore, equation (iii) becomes
log 1 = 0 – 1 + C
⇒ C = 1
Substituting C = 1 in equation (iii) we get
log |x – y| = x + y + 1
This is the required particular solution of the given differential equation.

Question 12.
Solve the differential equation \(\left[\frac{e^{-2 \sqrt{x}}}{\sqrt{x}}-\frac{y}{\sqrt{x}}\right] \frac{d x}{d y}\) = 1 (x ≠ 0)
Solution.

Question 13.
Find a particular solution of the differential equation \(\frac{d y}{d x}\) + y cot x = 4x cosec x (x ≠ 0),
given that y = 0 when x = \(\frac{\pi}{2}\).
Solution.
The given differential equation is \(\frac{d y}{d x}\) + y cot x = 4x cosec x
This equation is a linear differential equation of the form
\(\frac{d y}{d x}\) + Py = Q, (where P = cot x and Q = 4x cosec x)
Now, I.F. = e^{∫ P dx}
= e^{∫ cot x dx}
= e^{log |sin x|}
= sin x
The general solution of the given differential equation is given by
y (I.F.) = ∫ (Q × I.F.) dx + C
⇒ y sin x = ∫ (4x cosec x . sin x)dx + C
⇒ y sin x = 4 ∫ x dx + C
⇒ y sin x = 4\(\frac{x^{1+1}}{1+1}\) + C
⇒ y sin x = 4 . \(\frac{x^{2}}{2}\) + C
⇒ y sin x = 2x² + C …………..(i)
Now, y = 0 at x = \(\frac{\pi}{2}\)
Therefore, equation (i) becomes
0 = 2 × \(\frac{\pi^{2}}{4}\) + C

= C = \(\frac{\pi^{2}}{2}\)
Substituting C = – \(\frac{\pi^{2}}{2}\) in equation (i), we get
y sin x = 2x – \(\frac{\pi^{2}}{2}\).
This is the required particular solution of the given differential equation.

Question 14.
Find a particular solution of the differential equation (x + 1) \(\frac{d y}{d x}\) = 2e^{– y} – 1, given that y = 0 when x = 0.
Solution.
Given differential equation is (x + 1) \(\frac{d y}{d x}\) = 2e^{– y} – 1

Question 15.
The population of a village increases continuously at the rate proportional to the number of its inhabitants present at any time. If the population of the village was 20000 in 1999 and 25000 in the year 2004, what will be the population of the village in 2009?
Solution.
Let the population at any instant (t) be y.
It is given that the rate of increase of population is proportional to the number of inhabitants at any instant.
∴ \(\frac{d y}{d t}\) ∝ y
⇒ \(\frac{d y}{d t}\) = ky (k is a constant)
⇒ \(\frac{d y}{y}\) = k dt
Integrating both sides, we get
log y = kt + C …………..(i)
In the year 1999, t = 0 and y = 20000.
Therefore, we get
log 20000 C …………..(ii)
In the year 2004, t = 5 and y = 25000.
Therefore, we get
log 25000 = k.5 + C
⇒ log 25000 = 5k + log 20000
⇒ 5k = \(\log \left(\frac{25000}{20000}\right)=\log \left(\frac{5}{4}\right)\)
⇒ k = \(\frac{1}{5} \log \left(\frac{5}{4}\right)\) …………(i)
In the year 2009, t = 10 years.
Now, on substituting the values oft, k, and C in equation (i), we get
log y = 10 × \(\frac{1}{5} \log \left(\frac{5}{4}\right)\) + log (20000)
⇒ log y = log \(\left[20000 \times\left(\frac{5}{4}\right)^{2}\right]\)
⇒ y = 20000 × \(\frac{5}{4}\) × \(\frac{5}{4}\)
⇒ y = 31250
Hence, the population of the village in 2009 will be 31250.

Question 16.
The general solution of the differential equation \(\frac{y d x-x d y}{y}\) = 0
(A) xy = C
(B) x = Cy²
(C) y = Cx
(D) y = Cx²
Sol.
The given differential equation is \(\frac{y d x-x d y}{y}\) = 0
⇒ \(\frac{y d x-x d y}{y}\) = 0

⇒ \(\frac{1}{x} d x-\frac{1}{y} d x\) = 0
Integrating both sides, we get
log |x| – log |y| = log k

log |\(\frac{x}{y}\)| = log k
⇒ \(\frac{x}{y}\) = k
⇒ y = \(\frac{1}{k}\) x
⇒ y = Cx, where C = \(\frac{1}{k}\)
Hence, the correct answer is (C).

Question 17.
The general solution of a differential equation of the type \(\frac{d y}{d x}\) + P₁x = Q₁ is
(A) \(y e^{\int P_{1} d y}=\int\left(Q_{1} e^{\int P_{1} d y}\right) d y\) + C

(B) \(y \cdot e^{j P_{1} d x}=\int\left(Q_{1} e^{\int P_{1} d x}\right) d x\) + C

(C) \(x e^{\int P_{1} d y}=\int\left(Q_{1} e^{\int P_{1} d y}\right) d y\) + C

(D) \(x e^{\int P_{1} d x}=\int\left(Q_{1} e^{\int P_{1} d x}\right) d y\) + C
Solution.
The integrating factor of the given differential equation \(\frac{d y}{d x}\) + P₁x = Q₁ is e^{∫ P dx}
The general solution of the differential equation is given by
x (I.F.) = ∫ (Q × I.F.) dy + C
x . e^{∫ P dx} = ∫ (Q₁ e^{∫ P dx} ) dy + C
Hence, the correct answer is (C).

Question 18.
The general solution of the differential equation e^x dy + (ye^x +2x) dx = 0 is
(A) xe^y + x² = C
(B) xe^y + y² = C
(C) ye^x + x² = C
(D) ye^y + x² = C
Solution.
The given differential equation is e^x dy + (ye^x +2x) dx = 0
⇒ e^x \(\frac{d y}{d x}\) + y e^x + 2x = 0
⇒ \(\frac{d y}{d x}\) + y = – 2x e^{– x}
This is a linear differential equation of the form
\(\frac{d y}{d x}\) + Py = Q, (where P = 1 and Q = – 2xe^{– x})

Now, I.F.= e^{∫ P dx}
= e^{∫ 1 dx}
= e^x
The general solution of the given differential equation is given by
y(I.F.) = ∫ (Q × I.F.)dx + C
⇒ ye^x = ∫ (- 2xe^{– x} . e^x) dx + C
⇒ ye^x = – ∫ 2x dx + C
⇒ ye^x = – x² + C
⇒ ye^x + x² = C
Hence, the correct answer is (C).