PSEB 12th Class Physics Important Questions Chapter 2 Electrostatic Potential and Capacitance

Punjab State Board PSEB 12th Class Physics Important Questions Chapter 2 Electrostatic Potential and Capacitance Important Questions and Answers.

PSEB 12th Class Physics Important Questions Chapter 2 Electrostatic Potential and Capacitance

Very short answer type questions

Question 1.
A charge ‘q’ is moved from a point A above a dipole of dipole moment ‘p’ to a point B below the dipole in equatorial plane without acceleration. Find the work done in the process.

Answer:
Work done in the process is zero. Because, equatorial plane of a dipole is equipotential surface and work done in moving charge oh equipotential surface is zero.
W = qV_AB = q × 0 = 0

Question 2.
A point charge Q is placed at point O as shown in the figure. Is the potential difference (V_A – V_B) positive, negative or zero if Q is
(i) positive
(ii) negative

Answer:
Let the distance of points A and B from charge Q be r_A and r_B, respectively.
∴ Potential difference between points A and B
V_A – V_B = \(\frac{q}{4 \pi \varepsilon_{0}}\left[\frac{1}{r_{A}}-\frac{1}{r_{B}}\right]\)
As r_A = OA, r_B = r_B = OB
and r_A < r_B, \(\frac{1}{r_{A}}>\frac{1}{r_{B}}\)
There,[latex]\frac{1}{r_{A}}-\frac{1}{r_{B}}[/latex] has positive value.
(V_A – V_B) depends on the nature of charge q.
(V_A – V_B) is positive when Q > 0
(V_A – V_B ) is negative when Q < 0

Question 3.
A hollow metal sphere of radius 5 cm is charged such that potential on its surface is 10 V. What is the potential at the centre of the sphere?
Answer:
The electric potential at every point inside the charged spherical shell is same and equal to the electric potential on its surface.
The electric potential at the centre of sphere is 10 V.

Question 4.
Can two equipotential surfaces intersect each other? Justify your answer.
No, two equipotential surfaces cannot intersect each other because

1. Two normals can be drawn at intersecting point on two surfaces which gives two directions of E at the same point which is impossible.
2. Also two values of potential at the same point is not possible.

Question 5.
Why electrostatic potential is constant throughout the volume of the conductor and has the same value as on its surface?
Since, electric field intensity inside the conductor is zero. So, electrostatic potential is a constant.
But, E = –\(\frac{\Delta V}{\Delta r}\)
∴ E = 0, ΔV = 0
or V₂ – V₁ =0, V₂ – V₁
The potential at every point inside the conductor remains same.

Question 6.
In a certain 0.5 cm³ of space, electric potential is found to be 7 V throughout. What is the electric field in this region?
Answer:
Zero, because electric potential is same throughout as
E = \(\frac{d V}{d r}\)

Question 7.
Distinguish between a dielectric and a conductor.
Answer:
Dielectrics are non-conductors and do not have free electrons at all. While conductor has free electrons in its any volume which makes it able to pass the electricity through it.

Question 8.
The given graph shows the variation of charge q versus potential difference V for two capacitors C₁ and C₂. Both the capacitors have same plate separation but plate area of C₂ is greater than that C₁. Which line (A or B) corresponds to C₁ and why?

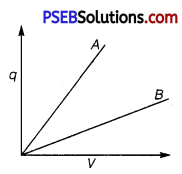
Answer:
Line B corresponds to Q because slope (q/V) of B is less than slope of A.

Question 9.
Do free electrons travel to region of higher potential or lower potential? (NCERT Exemplar)
Answer:
Free electrons would travel to regions of higher potentials as they are negatively charged.

Question 10.
Can there be a potential difference between two adjacent conductors carrying the same charge? (NCERT Exemplar)
Answer:
Yes, if the sizes are different.

Question 11.
Prove that, if an insulated, uncharged, conductor is placed near a charged conductor and no other conductors are present, the uncharged body must intermediate in potential between that of the charged body and that of infinity. (NCERT Exemplar)
Answer:
Let us take any path from the charged conductor to the uncharged conductor along the direction of electric field. Therefore, the electric potential decrease along this path.
Now, another path from the uncharged conductor to infinity will again continually lower the potential further. This ensures that the uncharged body must be intermediate in potential between that of the charged body and that of infinity.

Question 12.
A test charge q is made to move in the electric field of a point charge Q along two different closed paths [figure]. First path has sections along and perpendicular to lines of electric field.
Second path is a rectangular loop of the same area as the first loop. How does the work done compare in the two cases? (NCERT Exemplar)

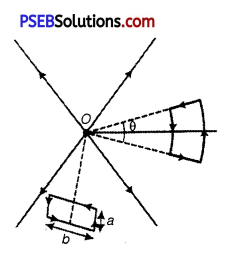
Answer:
As electric field is conservative, work done will be zero in both the cases.

Short answer type questions

Question 1.
What is electrostatic shielding? How is this property used in actual practice? Is the potential in the cavity of a charged conductor zero?
Answer:
Whatever be the charge and field configuration outside, any cavity in a conductor remains shielded from outside electric influence. The field inside a conductor is zero. This is known as electrostatic shielding.

• Sensitive instruments are shielded from outside electrical influences by enclosing them in a hollow conductor.
• During lightning it is safest to sit inside a car, rather than near a tree. The metallic body of a car becomes an electrostatic shielding from lightening.

Potential inside the cavity is not zero. Potential is constant.

Question 2.
Two capacitors of unknown capacitances C₁ and C₂ are connected first in series and then in parallel across a battery of 100 V. If the energy stored in the two combinations is 0.045 J and 0.25 J respectively, determine the value of C₁ and C₂. Also calculate the charge on each capacitor in parallel combination.
Answer:
Energy stored in a capacitor,

Q₁ = C₁V = 38.2 × 10^-6 × 100 = 38.2 × 10^-4 C
Q₂ = C₂V = 11.8 × 10^-6 × 100 = 11.8 × 10^-4C

Question 3.
Calculate the equivalent capacitance between points A and B in the circuit below. If a battery of 10 V is connected across A and B, calculate the charge drawn from the battery by the circuit.

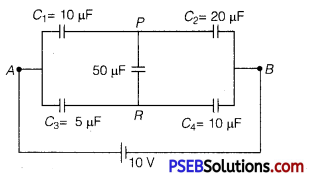
Answer:

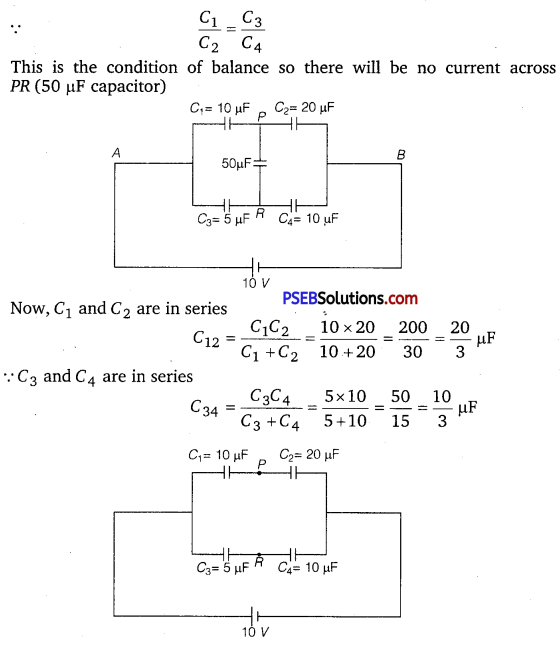
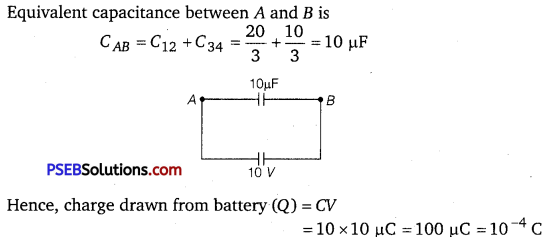
Question 4.
A parallel plate capacitor is charged by a battery to a potential. The battery is disconnected and a dielectric slab is inserted to completely fill the space between the plates.
How will
(a) its capacitance
(b) electric field between the plates and
(c) energy stored in the capacitor be affected? Justify your answer giving necessary mathematical expression for each case.
Answer:
On introduction of dielectric slab in a isolated charged capacitor.
(a) The capacitance (C’) becomes K times of original capacitor as
C = \(\frac{\varepsilon_{0} A}{d}\)
and C ‘ = \(\frac{K \varepsilon_{0} A}{d}\)

(b) The total charge on the capacitor remains conserved on introduction of dielectric slab. Also, the capacitance of capacitor increases to K times of original values.
∴ CV = C’V’
CV = (KC)V’
⇒ V’ = \(\frac{V}{K}\)
∴ New electrical field,
E’ = \(\frac{V^{\prime}}{d}=\left(\frac{V / K}{d}\right)=\left(\frac{V}{d}\right) \frac{1}{K}=\frac{E}{K}\)
∴ On introduction of dielectric medium new electric field E’ becomes \(\) times of its original value.
(c) Energy stored initially,
U = \(\frac{q^{2}}{2 C}\)
Energy stored later,
U’ = \(\frac{q^{2}}{2(K C)}\) [< C’ = KG]
where, K = dielectric constant of medium
⇒ U’ = \(\frac{1}{K}\left(\frac{q^{2}}{2 C}\right)\)
⇒ U’ = \(\frac{1}{K}\) × U
The energy stored in the capacitor decreases and becomes \(\frac{1}{K}\) times of original energy.

Question 5.
Two identical parallel plate capacitors A and B are connected to a battery of V volts with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant K. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.

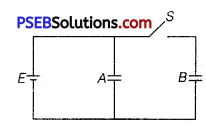
Answer:
Let C be the capacitance of each capacitor.
With switch S closed, the two capacitor are in parallel.
∴ Equivalent capacitance is 2 C.
∴ Energy stored = \(\frac{1}{2}\)(2C)V²
U₁ = CV² …………… (1)

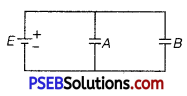
Now, when switch is opened and then free space of capacitors are filled with dielectric, the capacitance of each capacitor will be KC. For capacitor B, the charge will remain as before and for A, the potential difference will remain same.

Charge on each capacitor in the previous case will be CV.
∴ Energy stored in capacitor A in circuit case is

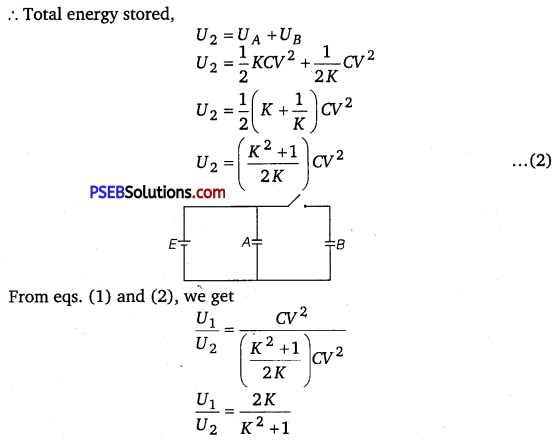
Question 6.
Consider two conducting spheres of radii R₁ and R₂ with R₁ > R₂. If the two are at the same potential, the larger sphere has more charge than the smaller sphere. State whether the charge density of the smaller sphere is more or less than that of the larger one. (NCERT Exemplar)
Answer:

Question 7.
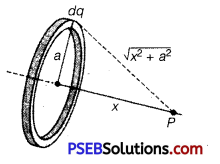
Calculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.
(NCERT Exemplar)
Answer:
Let us take point P to be at a distance x from the centre of the ring, as shown in figure. The charge element dq is at a distance x from point P. Therefore, V can be written as

Long answer type questions

Question 1.
(i) Explain using suitable diagrams, the difference in the behaviour of a
(a) conductor and
(b) dielectric in the presence of external electric field. Define the terms polarisation of a dielectric and write its relation with susceptibility.

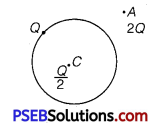
(ii) A thin metallic spherical shell of radius R carries a charge Q on its surface. A point charge \(\frac{Q}{2}\) is placed at its centre C and an other charge +2Q is placed outside the shell at a distance x from the centre as shown in the figure. Find (a) the force on the charge at the centre of shell and at the point A, (b) the electric flux through the shell.

Answer:
(i) When a capacitor is placed in an external electric field, the free charges present inside the conductor redistribute themselves in such a manner that the electric field due to induced charges opposes the external field within the conductor. This happens until a static- situation is achieved, i.e., when the two fields cancels each other and the net electrostatic field in the conductor becomes zero.

In contrast to conductors, dielectrics are non- conducting substances, i.e., they have no charge carriers. Thus, in a dielectric, free movement of charges is not possible. It turns out that the external field induces dipole moment by stretching molecules of the dielectric. The collective effect of all the molecular dipole moments is the net charge on the surface of the dielectric which produces a field that opposes the external field. However, the opposing field is so induced does not exactly cancel the external field, ft only reduces it. The extent of the effect depends on the nature of dielectric.

Both polar and non-polar dielectric develop net dipole moment in the presence of an external field. The dipole moment per unit volume is called polarisation and is denoted by P for linear isotropic dielectrics.
P = %E

(a) At point C, inside the shell.
The electric field inside a spherical shell is zero. Thus, the force experienced by charge at the centre C will also be zero.

Question 2.
(a) Find the ratio of the potential differences that must he applied across the parallel and series combination of two capacitors C ₁and C₂ with their capacitances in the ratio 1:2 so that the energy stored in the two cases becomes the same.

(b) Show that the potential energy of a dipole making angle θ with the direction of the field is given by u(θ) = – p \(\). Hence find out the amount of work done in rotating it from the position of unstable equilibrium to the stable equilibrium.

(b) As charges +q and -q traverse equal distance under equal and opposite forces; therefore, net work done in bringing the dipole in the region of electric field perpendicular to field-direction will be zero, i.e.,W₁ = 0.

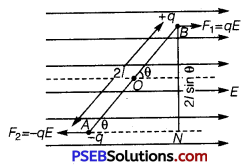
Now, the dipole is rotated and brought to orientation making an angle θ with the field direction (i.e., θ₀ = 90° and θ₁ = θ°), therefore, work done
W₂ = p_E (cosθ₀ – cosθ ₁)
= p_E (cos 90° – cos θ) = -pE cos θ

∴Total work done in bringing the electric dipole from infinity, i.e., electric potential energy of electric dipole. Thus, work done by external torque in rotating a dipole in uniform electric field is stored as the potential energy of the system.

U = W₁ + W₂ = 0 – pEcosθ
= -pE cosθ
In vector form
U = – \(\vec{p} \cdot \vec{E}\)
For rotating dipole from position of unstable equilibrium (θ₀ =180°) to the stable equilibrium (θ = 0°)
∴W = pE (cos 180° – cos0°)
= pE (-1 -1) = -2 pE