PSEB 5th Class Maths Solutions Chapter 10 ਅੰਕੜਾ ਵਿਗਿਆਨ Ex 10.1

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 10 ਅੰਕੜਾ ਵਿਗਿਆਨ Ex 10.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 10 ਅੰਕੜਾ ਵਿਗਿਆਨ Ex 10.1

ਪ੍ਰਸ਼ਨ 1.
ਇੱਕ ਸਕੂਲ ਦੇ ਬੱਚੇ ਪਿਕਨਿਕ ਲਈ ਚਿੜੀਆਘਰ ਗਏ । ਬੱਚਿਆਂ ਦੁਆਰਾ ਵੱਖ-ਵੱਖ ਜਾਨਵਰਾਂ ਦੀ ਗਿਣਤੀ ਦੇ ਅੰਕੜੇ ਇੱਕਤਰ ਕੀਤੇ ਗਏ, ਜਿਨ੍ਹਾਂ ਵਿੱਚੋਂ ਕੁਝ ਜਾਨਵਰਾਂ ਦੀ ਗਿਣਤੀ ਇਸ ਪ੍ਰਕਾਰ ਹੈ : ਬਾਂਦਰ-32, ਸ਼ੇਰ- 10, ਹਿਰਨ25, ਖਰਗੋਸ਼-27 ਅਤੇ ਲੂੰਬੜੀ-39 । ਇਹਨਾਂ ਅੰਕੜਿਆਂ ਨੂੰ ਸਾਰਣੀ ਦੇ ਰੂਪ ਵਿੱਚ ਪ੍ਰਗਟ ਕਰੋ ।


ਹੱਲ:
ਅਸੀਂ ਉਪਰੋਕਤ ਜਾਣਕਾਰੀ ਨੂੰ ਸਾਰਣੀ ਦੇ ਰੂਪ ਵਿਚ ਹੇਠਾਂ ਦਿੱਤੇ ਅਨੁਸਾਰ ਦਿਖਾ ਸਕਦੇ ਹਾਂ :

ਪ੍ਰਸ਼ਨ 2.
ਕਿਸੇ ਪਿੰਡ ਵਿੱਚ ਸਰਕਸ ਲੱਗੀ ਹੋਈ ਹੈ । ਸੋਮਵਾਰ ਤੋਂ ਸ਼ੁਕਰਵਾਰ ਤੱਕ ਸਰਕਸ ਦੇਖਣ ਆਏ ਬੱਚਿਆਂ ਦੀ ਗਿਣਤੀ ਚਿੱਤਰਫ਼ ਦੁਆਰਾ ਦਰਸਾਈ ਗਈ ਹੈ । ਹੇਠਾਂ ਦਿੱਤੇ ਚਿੱਤਰਫ਼ ਨੂੰ ਧਿਆਨ ਨਾਲ ਪੜ੍ਹ ਕੇ ਉੱਤਰ ਦਿਓ ।

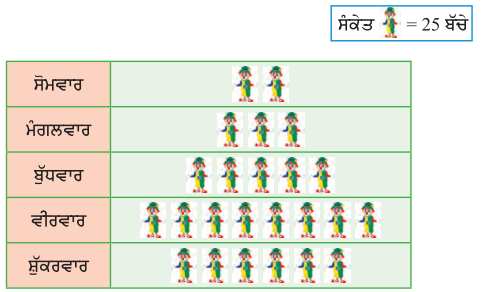
1. ਮੰਗਲਵਾਰ ਨੂੰ ਕਿੰਨੇ ਬੱਚੇ ਸਰਕਸ ਦੇਖਣ ਆਏ ?
2. ਕਿਸ ਦਿਨ ਸਭ ਤੋਂ ਵੱਧ ਬੱਚੇ ਸਰਕਸ ਦੇਖਣ ਆਏ ਅਤੇ ਕਿੰਨੇ ?
3. ਕਿਸ ਦਿਨ ਸਭ ਤੋਂ ਘੱਟ ਬੱਚੇ ਸਰਕਸ ਦੇਖਣ ਆਏ ਅਤੇ ਕਿੰਨੇ ?
4. ਸੋਮਵਾਰ ਅਤੇ ਬੁੱਧਵਾਰ ਨੂੰ ਕੁੱਲ ਕਿੰਨੇ ਬੱਚਿਆਂ ਨੇ ਸਰਕਸ ਦੇਖੀ ?
5. ਵੀਰਵਾਰ ਅਤੇ ਸ਼ੁੱਕਰਵਾਰ ਸਰਕਸ ਦੇਖਣ ਵਾਲੇ ਬੱਚਿਆਂ ਦੀ ਗਿਣਤੀ ਵਿੱਚ ਕਿੰਨਾ ਅੰਤਰ ਹੈ ?

ਹੱਲ:

1. ਮੰਗਲਵਾਰ ਨੂੰ 3 × 25 = 75 ਬੱਚੇ ਸਰਕਸ ਦੇਖਣ ਆਏ ।
2. ਵੀਰਵਾਰ ਨੂੰ ਸਭ ਤੋਂ ਵੱਧ, 8 × 25 = 200 . ਬੱਚੇ ਕਸ ਦੇਖਣ ਆਏ ।
3.  ਸੋਮਵਾਰ ਨੂੰ ਸਭ ਤੋਂ ਘੱਟ, 2 × 25 = 50 ਬੱਚੇ ਸਰਕਸ ਦੇਖਣ ਆਏ ।
4.  ਸੋਮਵਾਰ ਅਤੇ ਬੁੱਧਵਾਰ ਨੂੰ ਕੁੱਲ (2 +5) × 25 = 7 × 25 = 175 ਬੱਚਿਆਂ ਨੇ ਸਰਕਸ ਦੇਖੀ ।
5. ਵੀਰਵਾਰ ਅਤੇ ਸ਼ੁੱਕਰਵਾਰ ਸਰਕਸ ਦੇਖਣ ਵਾਲੇ , ਬੱਚਿਆਂ ਦੀ ਗਿਣਤੀ ਵਿੱਚ ਜਿੰਨਾ ਅੰਤਰ ਹੈ = 200 – 150 = 50.

ਪ੍ਰਸ਼ਨ 3.
ਪੰਜ ਵੱਖ-ਵੱਖ ਪਿੰਡਾਂ ਵਿੱਚ ਗਰੀਨ ਦਿਵਾਲੀ ਮਨਾਉਣ ਲਈ ਦਿਵਾਲੀ ਦੇ ਮੌਕੇ ਅੱਗੇ ਲਿਖੇ ਅਨੁਸਾਰ ਦਰੱਖ਼ਤ ਲਗਾਏ ਗਏ ।

(i) ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਲਈ ਚਿੱਤਰਗ੍ਰਾਫ਼ ਤਿਆਰ ਕੀਤਾ ਜਾਵੇ ।

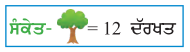
(ii) ਉਪਰੋਕਤ ਜਾਣਕਾਰੀ ਨੂੰ ਕੋਈ ਹੋਰ ਪੈਮਾਨਾ ਵਰਤ ਕੇ ਚਿੱਤਰਫ਼ ਤਿਆਰ ਕੀਤਾ ਜਾਵੇ ।
ਹੱਲ:
(i)

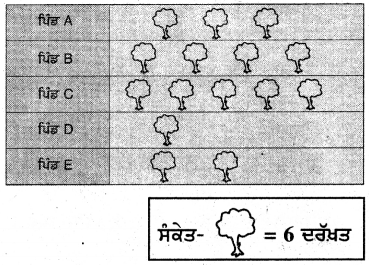
(ii)

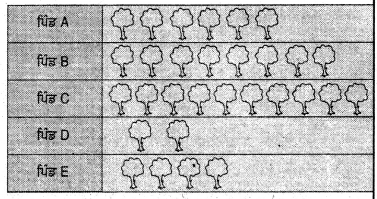
ਪ੍ਰਸ਼ਨ 4.
ਤਿਉਹਾਰਾਂ ਮੌਕੇ ਕਿਸੇ ਮਿਠਾਈ ਦੀ ਦੁਕਾਨ ਵਿੱਚ ਇੱਕ ਹਫ਼ਤੇ ਵਿੱਚ ਵਰਤੇ ਗਏ ਦੁੱਧ ਦੀ ਮਾਤਰਾ ਹੇਠਾਂ ਦਿੱਤੇ ਛੜ ਗ੍ਰਾਫ਼ ਅਨੁਸਾਰ ਹੈ ।

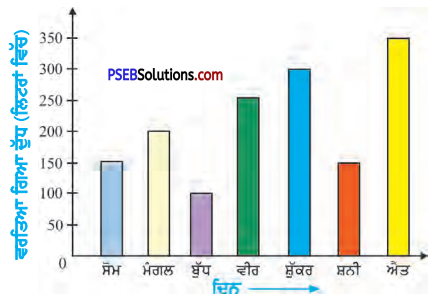
1.  ਸਭ ਤੋਂ ਵੱਧ ਦੁੱਧ ਕਿਹੜੇ ਦਿਨ ਵਰਤਿਆ ਗਿਆ ?
2.  ਸਭ ਤੋਂ ਘੱਟ ਦੁੱਧ ਕਿਹੜੇ ਦਿਨ ਵਰਤਿਆ ਗਿਆ ?
3. ਕਿਹੜੇ ਦੋ ਦਿਨਾਂ ਦੌਰਾਨ ਇੱਕੋ ਜਿਹੀ ਮਾਤਰਾ ਵਿੱਚ ਦੁੱਧ ਵਰਤਿਆ ਗਿਆ ਅਤੇ ਕਿੰਨਾ ?
4. ਵੀਰਵਾਰ ਅਤੇ ਸ਼ੁੱਕਰਵਾਰ ਨੂੰ ਕੁੱਲ ਕਿੰਨਾ ਦੁੱਧ ਵਰਤਿਆ ਗਿਆ ?
5. ਐਤਵਾਰ ਨਾਲੋਂ ਮੰਗਲਵਾਰ ਨੂੰ ਕਿੰਨਾ ਘੱਟ ਦੁੱਧ ਵਰਤਿਆ ਗਿਆ ?
6. ਸਭ ਤੋਂ ਵੱਧ ਵਰਤੇ ਗਏ ਦੁੱਧ ਅਤੇ ਸਭ ਤੋਂ ਘੱਟ ਵਰਤੇ ਗਏ ਦੁੱਧ ਦਾ ਅੰਤਰ ਕਿੰਨਾ ਹੈ ?

ਹੱਲ:

1. ਐਤਵਾਰ,
2. ਬੁੱਧਵਾਰ,
3. ਸੋਮਵਾਰ ਅਤੇ ਸ਼ਨਿਚਰਵਾਰ,
4. 550
5. 350 l – 200 l = 150 l
6. 350 l – 100 l = 250 l.

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਦੁਕਾਨ ‘ਤੇ ਅਕਤੂਬਰ ਮਹੀਨੇ ਵਿੱਚ ਵੇਚੇ ਗਏ ਵੱਖ-ਵੱਖ ਕੰਪਨੀਆਂ ਦੇ ਮੋਬਾਇਲ ਸੈਂਟਾਂ ਦਾ ਵੇਰਵਾ ਹੇਠਾਂ ਦਿੱਤੇ ਅਨੁਸਾਰ ਹੈ :

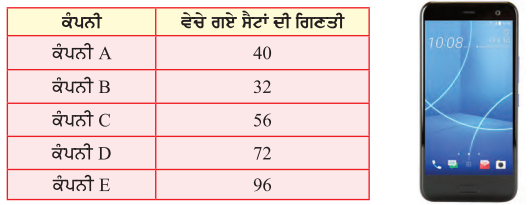
ਉਪਰੋਕਤ ਜਾਣਕਾਰੀ ਨੂੰ ਦਰਸਾਉਂਦਾ ਛੜ ਫ਼ ਤਿਆਰ ਕੀਤਾ ਜਾਵੇ ।
ਸੰਕੇਤ – 8 ਸੈਟਾਂ ਦਾ ਪੈਮਾਨਾ ਲਿਆ ਜਾਵੇ
ਹੱਲ:

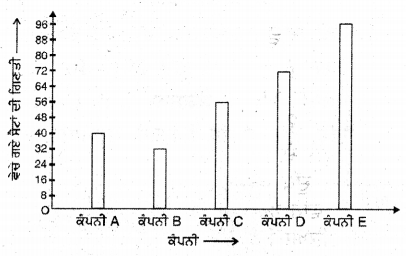
ਪ੍ਰਸ਼ਨ 6.
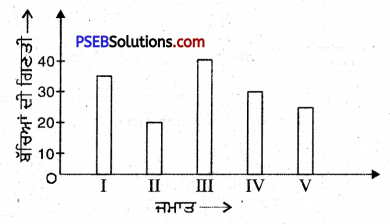
ਕਿਸੇ ਸਕੂਲ ਵਿੱਚ ਪਹਿਲੀ ਜਮਾਤ ਤੋਂ ਪੰਜਵੀਂ ਜਮਾਤ ਤੱਕ ਦੇ ਬੱਚਿਆਂ ਦੀ ਗਿਣਤੀ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ :

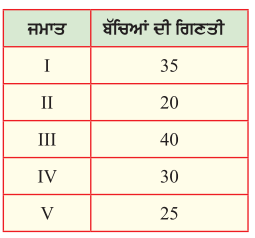
ਉਪਰੋਕਤ ਜਾਣਕਾਰੀ ਨੂੰ ਦਰਸਾਉਂਦਾ ਛੜ ਗ੍ਰਾਫ਼ ਤਿਆਰ ਕੀਤਾ ਜਾਵੇ ।
ਸੰਕੇਤ – 10 ਬੱਚਿਆਂ ਦੀ ਗਿਣਤੀ ਦਾ ਪੈਮਾਨਾ ਲਿਆ ਜਾਵੇ ।
ਹੱਲ:

ਪ੍ਰਸ਼ਨ 7.

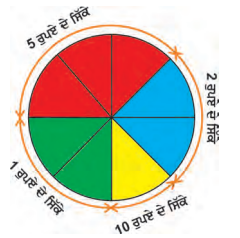
ਉਪਰੋਕਤ ਪਾਈ ਚਾਰਟ ਨੂੰ ਅੱਠ ਬਰਾਬਰ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ ਹੈ । ਇਹ ਅਜੇ ਦੀ ਗੋਲਕ ਵਿੱਚ ਵੱਖ-ਵੱਖ ਸਿੱਕਿਆਂ ਦੀ ਗਿਣਤੀ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ ।
ਹੇਠਾਂ ਲਿਖੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਦਿਓ :

1. ਤੋਂ 5 ਦੇ ਸਿੱਕਿਆਂ ਦੀ ਗਿਣਤੀ (ਭਿੰਨਾਤਮਕ ਰੂਪ ਵਿੱਚ ਕਿੰਨੀ ਹੈ ? ਜੇਕਰ ਸਿੱਕਿਆਂ ਦੀ ਕੁੱਲ ਗਿਣਤੀ 80 ਹੋਵੇ ।
2. ਤੋਂ 2 ਦੇ ਸਿੱਕਿਆਂ ਦੀ ਗਿਣਤੀ ਕਿੰਨੀ ਹੈ ?
3. ਤੋਂ 5 ਦੇ ਸਿੱਕਿਆਂ ਦੀ ਗਿਣਤੀ ਦੱਸੋ ?
4. ਤੋਂ 10 ਦੇ ਸਿੱਕਿਆਂ ਦੀ ਰਾਸ਼ੀ ਕਿੰਨੀ ਬਣਦੀ ਹੈ ?
5. ਅਜੇ ਦੀ ਗੋਲਕ ਵਿੱਚ ਕੁੱਲ ਕਿੰਨੀ ਰਾਸ਼ੀ ਹੈ ?

ਹੱਲ :
1. \(\frac{3}{8}\)

2. \(\frac{2}{8}\) × 80 = 20

3. \(\frac{3}{8}\) × 80 = 30

4. ₹ 10 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦੀ ਗਿਣਤੀ = \(\frac{1}{8}\) × 80 = 10
₹ 10 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦਾ ਕੁੱਲ ਮੁੱਲ
= ₹ 10 × 10 = ₹ 100

5. ₹ 1 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦੀ ਗਿਣਤੀ = \(\frac{2}{8}\) × 80 = 20
₹ 2 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦੀ ਗਿਣਤੀ = 20
₹ 5 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦੀ ਗਿਣਤੀ = 30
₹ 10 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦੀ ਗਿਣਤੀ = 10
₹ 1 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦਾ ਮੁੱਲ = ₹ 1 × 20 = ₹ 20
₹ 2 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦਾ ਮੁੱਲ = ₹ 2 × 20 = ₹ 40
₹ 5 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦਾ ਮੁੱਲ = ₹ 5 × 30 = ₹ 150
₹ 10 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦਾ ਮੁੱਲ = ₹ 10 ×x 10 = ₹ 100
ਅਜੇ ਦੀ ਗੋਲਕ ਵਿੱਚ ਜਿੰਨੀ ਰਾਸ਼ੀ ਹੈ : = ₹ 20 + ₹ 40 + ₹ 150 + 100
= ₹ 310.

ਪ੍ਰਸ਼ਨ 8.
ਦਿੱਤੇ ਗਏ ਪਾਈ ਚਾਰਟ ਨੂੰ 12 ਬਰਾਬਰ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ ਹੈ। ਦਿੱਤਾ ਗਿਆ ਪਾਈ ਚਾਰਟ ਕਿਸੇ ਸਕੂਲ ਦੇ 120 ਬੱਚਿਆਂ ਦੇ ਵੱਖੋਵੱਖਰੇ ਮਨਪਸੰਦ ਤਿਉਹਾਰਾਂ ਨੂੰ ਦਰਸਾ ਰਿਹਾ ਹੈ । ਇਸ ਨੂੰ ਧਿਆਨ ਨਾਲ ਪੜ੍ਹ ਕੇ ਹੇਠਾਂ ਦਿੱਤੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਦਿਓ ।

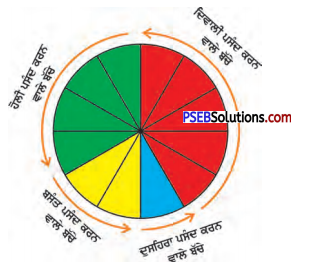
1. ਕਿੰਨੇ ਬੱਚਿਆਂ ਨੂੰ (ਭਿੰਨਾਤਮਕ ਰੂਪ ਵਿੱਚ ਦਿਵਾਲੀ ਦਾ ਤਿਉਹਾਰ ਪਸੰਦ ਹੈ ?
2. ਸਕੂਲ ਦੇ ਕੁੱਲ 120 ਬੱਚਿਆਂ ਵਿੱਚੋਂ ਹੋਲੀ ਦਾ ਤਿਉਹਾਰ ਪਸੰਦ ਕਰਨ ਵਾਲੇ ਬੱਚਿਆਂ ਦੀ ਗਿਣਤੀ ਕਿੰਨੀ ਹੈ ?
3. ਸਭ ਤੋਂ ਘੱਟ ਮਨਪਸੰਦ ਤਿਉਹਾਰ ਕਿਹੜਾ ਹੈ ?
4. ਦਿਵਾਲੀ ਅਤੇ ਬਸੰਤ ਪਸੰਦ ਕਰਨ ਵਾਲੇ ਬੱਚਿਆਂ ਦੀ ਗਿਣਤੀ ਦਾ ਅੰਤਰ ਕਿੰਨਾ ਹੈ ?

ਹੱਲ:

1. \(\frac{5}{12}\)
2.  \(\frac{4}{12}\) × 120 = 40
3.  ਦੁਸਹਿਰਾ
4.  (\(\frac{5}{12}\) – \(\frac{2}{12}\)) × 120
   = \(\frac{3}{12}\) × 120 = 30