Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 3 Playing with Numbers Ex 3.5 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 6 Maths Chapter 3 Playing with Numbers Ex 3.5
1. Find LCM of following numbers by prime factorization method:
Question (i)
45, 60
Solution:
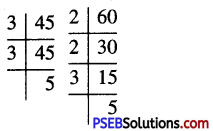
∴ 45 = 3 × 3 × 5
60 = 2 × 2 × 3 × 5
We find that in these prime factorizations, 2 occurs maximum two times, 3 occurs maximum two times and 5 occurs maximum once
∴ L.C.M. of 45 and 60
= 2 × 2 × 3 × 3 × 5 = 180
![]()
Question (ii)
52, 56
Solution:

We find that in these prime fatorisation, 2 occurs maximum 3 times, 13 and 7 occurs maximum once.
∴ L.C.M. of 52 and 56
= 2 × 2 × 2 × 13 × 7 = 728
Question (iii)
96, 360
Solution:
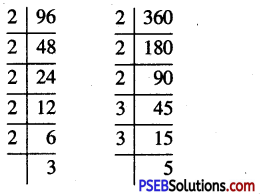
∴ 96 = 2 × 2 × 2 × 2 × 2 × 3
360 = 2 × 2 × 2 × 3 × 3 × 5
We find that in these prime factorisation, 2 occurs maximum 5 times, 3 occurs maximum 2 times and 5 occurs maximum once.
∴ L.C.M. of 96 and 360
= 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5 = 1440
Question (iv)
36, 96, 180
Solution:
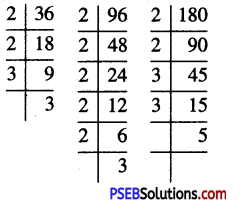
∴ 36 = 2 × 2 × 3 × 3
96 = 2 × 2 × 2 × 2 × 2 × 3
and 180 = 2 × 2 × 3 × 3 × 5
We find that in these factorisation, 2 occurs maximum 5 times, 3 occurs maximum 2 times and 5 occurs maximum once.
∴ L.C.M. of 36, 96 and 182
= 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5 = 1440
Question (v)
18, 42, 72.
Solution:
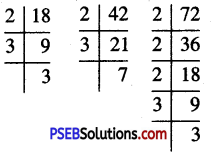
∴ 18 = 2 × 3 × 3
42 = 2 × 3 × 7
72 = 2 × 2 × 2 × 3 × 3
We find that in these factorization 2 occurs maximum 3 times, 3 occurs maximum 2 times and 7 occurs maximum once.
∴ L.C.M. of 18, 42 and 72
= 2 × 2 × 2 × 3 × 3 × 7 = 504
![]()
2. Find LCM of the following by common division method:
Question (i)
24, 64
Solution:

∴ L.C.M. of 24, 64
= 2 × 2 × 2 × 3 × 8 = 192
Question (ii)
42, 63
Solution:

∴ L.C.M. of 42 and 63
= 3 × 7 × 2 × 3 = 126
Question (iii)
108, 135, 162
Solution:

∴ L.C.M. of 108, 135 and 162
= 2 × 3 × 3 × 3 × 2 × 5 × 3 = 1620
Question (iv)
16, 18, 48
Solution:

∴ L.C.M. of 16, 18 and 48
= 2 × 2 × 2 × 2 × 3 × 3 = 144
![]()
Question (v)
48, 72, 108
Solution:

∴ L.C.M. of 48, 72 and 108
= 2 × 2 × 2 × 3 × 3 × 2 × 3 = 144
3. Find the smallest number which is divisible by 6, 8 and 10.
Solution:
We know that the smallest number divisible by 6, 8 and 10 is their L.C.M.
So, we calculate L.C.M. 6, 8 and 10

∴ L.C.M. = 2 × 3 × 4 × 5 = 120
Hence, required number =120
4. Find the least number when divided by 10,12 and 15 leaves remainder 7 in each case.
Solution:
We know that the least number divisible by 10, 12 and 15 is their L.C.M.

So, the required number will be 7 more than their L.C.M.
We calculate their L.C.M.
L.C.M of 10, 12 and 15 = 2 × 3 × 5 × 2 = 60
Hence, Required number = 60 + 7 = 67
![]()
5. Find the greatest 4-digit number exactly divisible by 12, 18 and 30.
Solution:
First find the L.C.M. of 12, 18, 30

∴ L.C.M. of 12, 18, 30
= 2 × 3 × 2 × 3 × 5 = 180
Now the greatest 4 digit number = 9999
We find that when 9999 is divided by 180, the remainder is 99.
Hence, the greatest number of 4 digits which is exactly divisible by 12, 18, 30
= 9999 – 99 = 9900
6. Find the sandiest 4-digit number exactly divisible by 15, 24 and 36.
Solution:
First find L.C.M. of 15, 24, 36

L.C.M. of 15, 24, 36
= 2 × 2 × 3 × 5 × 2 × 3 = 360 Now, 4 digit smallest number is 1000 We find that when 1000 is divided by 360, the remainder is 280.
∴ Smallest 4 digits number, which is exactly divisible by 15, 24 and 36
= 1000 + (360 – 280) = 1000 + 80 = 1080.
Hence, required number = 1080
![]()
7. Four bells toll at intervals of 4, 7, 12 and 14 seconds. The bells toll together at 5 a.m. When will they again toll together?
Solution:
The bells will toll together at a time which is multiple of four intervals 4, 7, 12 and 14 seconds
So, first we find L.C.M. of 4, 7, 12 and 14

∴ L.C.M. = 2 × 2 × 7 × 3 = 84
Thus the bells will toll together after 84 seconds or 1 minute 24 seconds.
First they toll together at 5 a.m., then they will toll together after 1 minutes 24 seconds i.e. 5 : 01 : 24 a.m.
8. Three boys step off together from the same spot their steps measures 56 cm, 70 cm and 63 cm respectively. At what distance from the starting point will they again step together?
Solution:
The distance covered by each one of them has to be same as well as minimum walk So, the minimum distance each should their steps will be L.C.M. of the distances L.C.M. of the measure of their steps.

∴ L.C.M. = 2 × 7 × 4 × 5 × 9 = 2520cm
Hence, the will again step to gether after a distance of 2520 cm.
9. Can two numbers have 15 as their HCF and 65 as their LCM. Give reasons in support of your answer.
Solution:
We know that H.C.F. of given numbers is a factor of their L.C.M.
But 15 is not a factor of 65
So, there can not be two numbers with H.C.F. 15 and L.C.M. 65.
![]()
10. Can two numbers have 12 as their HCF and 72 as their LCM. Give reasons in support of your answer.
Solution:
We know that H.C.F. of given numbers is a factor of their L.C.M.
Here, 12 divides 72 exactly. So 12 is a factor of 72
Hence, there can be two numbers with H.C.F. 12 and L.C.M 72.
11. The HCF and LCM of two numbers are 13 and 182 respectively. If one of the numbers is 26. Find other numbers.
Solution:
H.C.F. = 13 and L.C.M. = 182,
1st number = 25
Now, 1st number × 2nd number = H.C.F. × L.C.M.
26 × 2nd number = 13 × 182
∴ 2nd number = \(\frac {13×182}{26}\)
= 91
12. The LCM of two co-prime numbers is 195. If one number is 15 then find the other number.
Solution:
L.C.M. of two co-prime numbers = 195
H.C.F. of two co-prime numbers = 1
One number = 15
1st number × 2nd number = H.C.F. × L.C.M.
15 × 2nd number= 1 × 195
∴ 2nd number = \(\frac {1×195}{15}\)
= 13
![]()
13. The H.C.F. of two numbers is 6 and product of two numbers is 216. Find their L.C.M.
Solution:
H.C.F. of two numbers = 6
Product of two numbers = 216
We know that
H.C.F. × L.C.M. = Product of two numbers
∴ 6 × L.C.M. = 216
∴ L.C.M. = \(\frac {216}{6}\) = 36
