Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 8 Basic Geometrical Concepts Ex 8.3 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 6 Maths Chapter 8 Basic Geometrical Concepts Ex 8.3
1. Name the given angles in all ways:
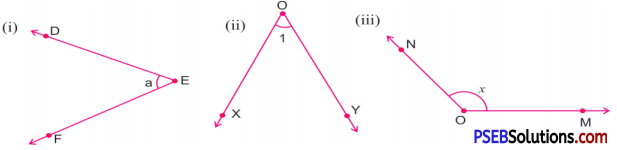
Solution:
(i) \(\angle \mathrm{DEF}, \angle \mathrm{FED}, \angle \mathrm{E}, \angle a\)
(ii) \(\angle \mathrm{XOY}, \angle \mathrm{YOX}, \angle \mathrm{O}, \angle 1\)
(iii) \(\angle N O M, \angle M O N, \angle O, \angle x\)
![]()
2. Name the vertex and the arms of given angles:
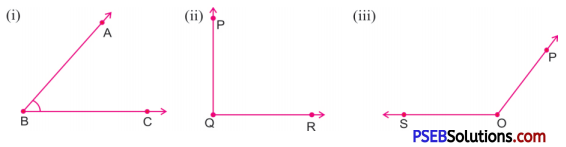
Solution:
| (i) | (ii) | (iii) | |
| Vertex | B | Q | o |
| Arm | \(\overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{BA}}\) | \(\overrightarrow{\mathrm{QP}}, \overrightarrow{\mathrm{QR}}\) | \(\overrightarrow{\mathrm{OS}}, \overrightarrow{\mathrm{OP}}\) |
3. Name all the angles of the given figure:
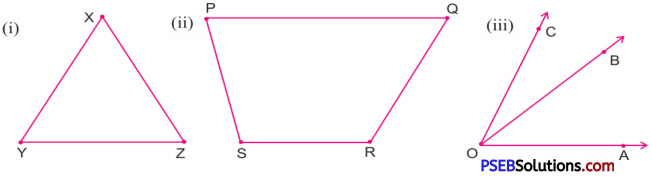
Solution:
(i) \(\angle \mathrm{X}, \angle \mathrm{Y}, \angle \mathrm{Z}\)
(ii) \(\angle \mathrm{P}, \angle \mathrm{Q}, \angle \mathrm{R}, \angle \mathrm{S}\)
(iii) \(\angle \mathrm{AOB}, \angle \mathrm{BOC}, \angle \mathrm{AOC}\)
![]()
4. In the given figure, name the points that lie:
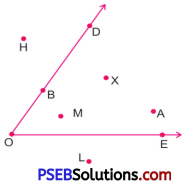
Question (i)
In the interior of \(\angle \mathrm{DOE}\)
Solution:
Points in the interior of \(\angle \mathrm{DOE}\) are :
A, X, M
Question (ii)
In the exterior of \(\angle \mathrm{DOE}\)
Solution:
Points in the exterior of \(\angle \mathrm{DOE}\) are :
H, L
Question (iii)
On the \(\angle \mathrm{DOE}\)
Solution:
Points on the \(\angle \mathrm{DOE}\) are :
D, B, O, E.
![]()
5. In the given figure, write another name for the following angles :
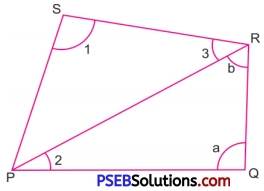
Question (i)
\(\angle \mathrm{1}\)
Solution:
\(\angle S \text { or } \angle PSR \text { or } \angle RSP\)
Question (ii)
\(\angle \mathrm{2}\)
Solution:
\(\angle \mathrm{RPQ} \text { or } \angle \mathrm{QPR}\)
Question (iii)
\(\angle \mathrm{3}\)
Solution:
\(\angle \mathrm{SRP} \text { or } \angle \mathrm{PRS}\)
Question (iv)
\(\angle \mathrm{a}\)
Solution:
\(\angle \mathrm{Q} \text { or } \angle \mathrm{RQP} \text { or } \angle \mathrm{PQR}\)
![]()
Question (v)
\(\angle \mathrm{b}\)
Solution:
\(\angle \mathrm{PRQ} \text { or } \angle \mathrm{QRP}\)
