Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 9 Understanding Elementary Shapes Ex 9.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 6 Maths Chapter 9 Understanding Elementary Shapes Ex 9.2
1. Classify the angles as acute, obtuse, right, straight or reflex angles:
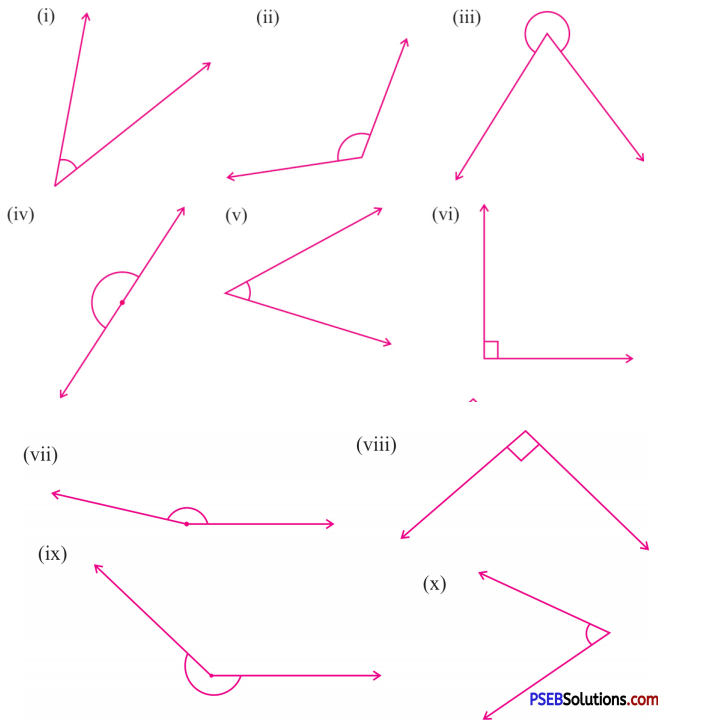
Solution:
(i) Acute angle
(ii) Obtuse angle
(iii) Reflex angle
(iv) Straight angle
(v) Acute angle
(vi) Right angle
(vii) Obtuse angle
(viii) Right angle
(ix) Reflex angle
(x) Acute angle.
![]()
2. Classify the angles:
Question (i)
80°
Solution:
80° is between 0° and 90°.
∴ It is an acute angle.
Question (ii)
172°
Solution:
172° is between 90° and 180°
∴ It is an obtuse angle.
Question (iii)
90°
Solution:
90° is a right angle.
Question (iv)
0°
Solution:
0° is a zero angle.
Question (v)
179°
Solution:
179° is between 90° and 180°.
∴ It is an obtuse angle.
![]()
Question (vi)
215°
Solution:
215° is between 180° and 360°.
∴ It is an reflex angle.
Question (vii)
360°
Solution:
360° is a complete angle.
Question (viii)
350°
Solution:
350° is between 180° and 360°.
∴ It is a reflex angle.
Question (ix)
15°
Solution:
15° is between 0° and 90°.
∴ It is an acute angle.
Question (x)
180°
Solution:
180° is a straight angle.
![]()
3. Measure the following angles with protractor and write their measurement:
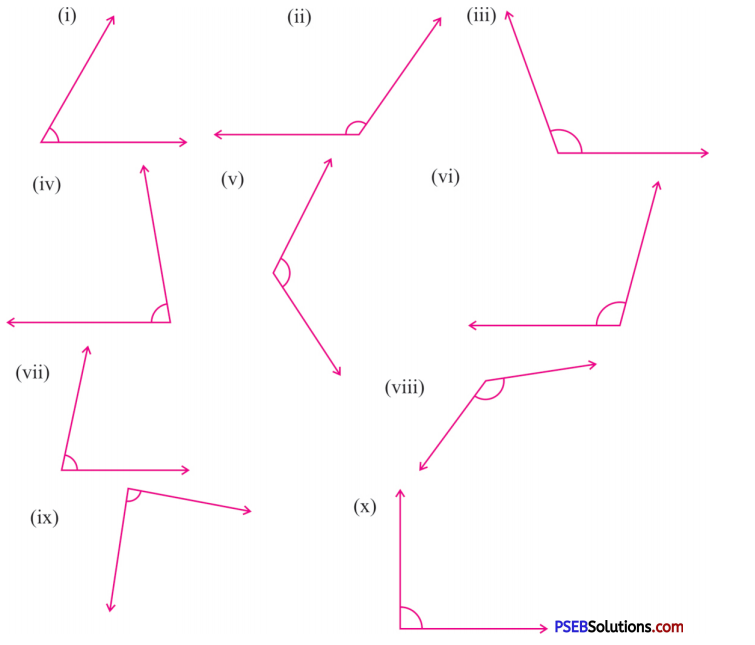
Solution:
(i) 60°
(ii) 125°
(iii) 110°
(iv) 80°
(v) 120°
(vi) 105°
(vii) 80°
(viii) 135°
(ix) 88°
(x) 90°.
4. How many degrees are there in
Question (i)
Two right angles
Solution:
1 right angle = 90°
∴ Two right angles = 2 × 90°
= 180°
![]()
Question (ii)
\(\frac {2}{3}\) right angles
Solution:
1 right angle = 90°
∴ \(\frac {2}{3}\) right angles = \(\frac {2}{3}\) × 90°
= 2 × 30°
= 60°
Question (iii)
Four right angles?
Solution:
1 right angle = 90°
∴ Four right angles = 4 × 90°
= 360°
5. What fraction of a clockwise revolution does the hour hand of a clock turn through when it goes from:
Question (i)
3 to 9
Solution:
3 to 9 : Half or \(\frac {1}{2}\)
Question (ii)
5 to 8
Solution:
5 to 8 : Quarter or \(\frac {1}{4}\)
Question (iii)
10 to 4
Solution:
10 to 4 : Half or \(\frac {1}{2}\)
![]()
Question (iv)
2 to 11
Solution:
2 to 11 : 3 Quarters or \(\frac {3}{4}\)
Question (v)
6 to 3
Solution:
6 to 3 : 3 Quarters or \(\frac {3}{4}\)
Question (vi)
2 to 7.
Solution:
2 to 7 : \(\frac {5}{12}\)
6. Find the number of right angles turned through by the hour hand of a dock when it goes from
Question (i)
5 to 8
Solution:
5 to 8 : 1 right angle
Question (ii)
1 to 7
Solution:
1 to 7 : 2 right angles
Question (iii)
4 to 10
Solution:
4 to 10 : 2 right angles
![]()
Question (iv)
9 to 12
Solution:
9 to 12 : 1 right angles
Question (v)
11 to 2
Solution:
11 to 2 : 1 right angles
Question (vi)
9 to 6
Solution:
9 to 6 : 3 right angles
Question (vii)
2 to 11
Solution:
2 to 11 : 3 right angles
Question (viii)
10 to 1
Solution:
10 to 1 : 1 right angles
Question (ix)
12 to 6
Solution:
12 to 6 : 2 right angles
![]()
Question (x)
5 to 2.
Solution:
5 to 2 : 3 right angles.
7. Where will be the hand of a clock stop if it starts at:
Question (i)
12 and make \(\frac {1}{4}\) revolution clock-wise.
Solution:
For 1 revolution, the hour hand takes 12 hours.
For \(\frac {1}{4}\) revolution, the hour hand takes \(\frac {1}{4}\) × 12 hours = 3 hours.
If hour hand starts at 12 and make \(\frac {1}{4}\) revolution clockwise it will stop at 3.
Question (ii)
2 and make \(\frac {1}{2}\) revolution clock-wise.
Solution:
For 1 revolution, the hour hand takes 12 hours.
For \(\frac {1}{2}\) revolution, the hour hand takes \(\frac {1}{2}\) × 12 hours = 6 hours.
If hour hand starts at 2 and make \(\frac {1}{2}\) revolution clockwise it will stop at 8.
![]()
Question (iii)
5 and make \(\frac {1}{4}\) revolution clock-wise.
Solution:
For 1 revolution, the hour hand takes 12 hours.
For \(\frac {1}{4}\) revolution, the hour hand takes \(\frac {1}{4}\) × 12 hours = 3 hours
If hour hand starts at 5 and make \(\frac {1}{4}\) revolution clockwise it will stop at 8.
Question (iv)
5 and make \(\frac {3}{4}\) revolution clock-wise.
Solution:
For 1 revolution, the hour hand takes 12 hours .
For \(\frac {3}{4}\) revolution, the hour hand takes \(\frac {3}{4}\) × 12 hours = 9 hours.
If hour hand starts at 5 and make \(\frac {3}{4}\) revolution clockwise it will stop at 2.
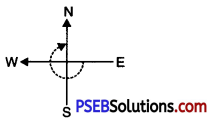
8. What part of revolution have you turned through if you stand facing:
Question (i)
East and turn clockwise to North
Solution:
I turned through \(\frac {3}{4}\) part of a revolution.
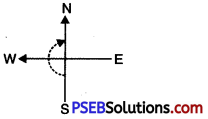
Question (ii)
South and turn clockwise to North
Solution:
I turned through \(\frac {1}{2}\) part of a revolution.
![]()
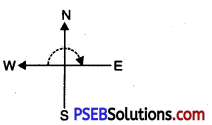
Question (iii)
South and turn clockwise to East
Solution:
I turned through \(\frac {3}{4}\) part of a revolution.
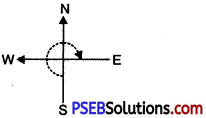
Question (iv)
West and turn clockwise to East
Solution:
I turned through \(\frac {1}{2}\) part of at revolution.
9. Find the angle measure between the hands of the clock in each figure:
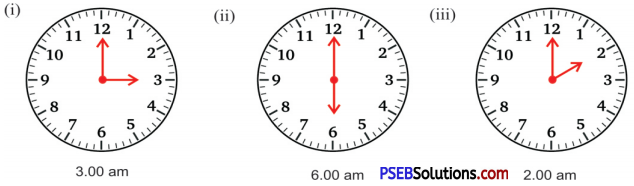
Solution:
(i) Angle measure between the hands of the clock at 3.00 a.m.
= \(\frac {3}{12}\) × 360° = 90°
(ii) Angle measure between the hands of the clock at 6.00 a.m.
= \(\frac {6}{12}\) × 360° = 180°
(iii) Angle measure between the hands of the clock at 2.00 a.m.
= \(\frac {2}{12}\) × 360° = 60°
![]()
10. Draw the following angles by protractor:
Question (i)
(i) 40°
(ii) 75°
(iii) 105°
(iv) 90°
(v) 130°
Solution:
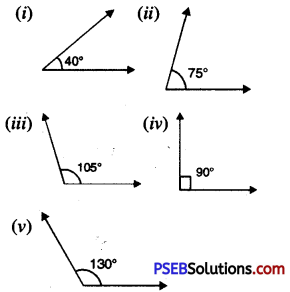
11. State true or false:
Question (i)
The sum of two right angles is always a straight angle.
Solution:
True
![]()
Question (ii)
The sum of two acute angles is always a reflex angle.
Solution:
False
Question (iiii)
The obtuse angle has measurement between 90° to 180°.
Solution:
True
Question (iv)
A complete revolution has four right angles.
Solution:
True
12. Fill in the blanks:
Question (i)
The angle which is greater than 0° and less than 90° is called ………….. .
Solution:
acute angle
![]()
Question (ii)
The angle whose measurement equal to two right angle is …………….. .
Solution:
straight angle
Question (iii)
The angle between 90° and 180° is ……………. .
Solution:
obtuse angle.
