Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 10 Practical Geometry Ex 10.4 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 10 Practical Geometry Ex 10.4
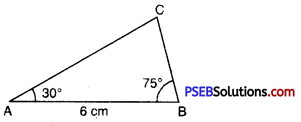
1. Construct ΔABC, given AB = 6 cm, ∠A = 30° and ∠B = 75°.
Solution:
Given. One side of ΔABC as AB = 6 cm, m∠A = 30° and m∠B = 75°.
To construct: A triangle with one side and these two angles.
Steps of Construction :
Step 1. We first draw a rough sketch of ΔABC and indicate the measures of side and two angles.
Step 2. Draw a ray AB of length 6 cm.
![]()
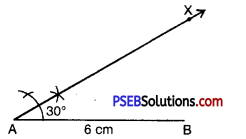
Step 3. At A; draw a ray AX making an angle 30° with AB.
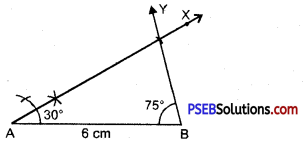
Step 4. With the help of compass. At B; draw a ray BY making an angle of 75° with AB.
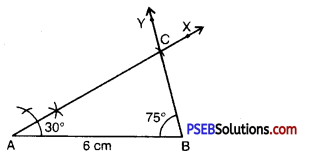
Step 5. Both rays AX and BY intersect, at a point. So the point of intersection of the two rays is C Then. ΔABC is now obtained.
![]()
2. Construct an isosceles ΔABC such that AB = 5.3 cm and each base angle = 45°.
Solution:
Given : Isosceles ΔABC with AB = 5.3 cm each base angle = 45°.
To Construct: A triangle with one side and two base angles.
Steps of construction :
Step 1. Draw a rough sketch of ΔABC with given measures
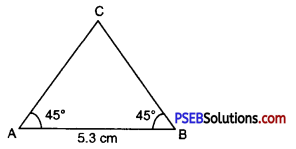
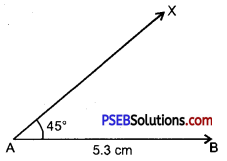
Step 2. Draw a line segment AB = 5.3 cm.
![]()
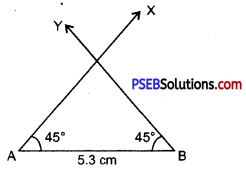
Step 3. Taking A as centre with the help of compass. Draw a ray AX making an angle 45° with AB.
Step 4. With the help of compass and taking B as a centre. Draw a ray BY making an angle 45° with the line segment AB.
Step 5. Rays AX and BY intersect, at a point say C, then ABC is the required triangle.
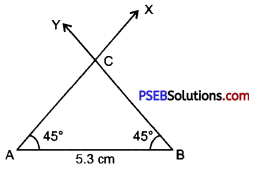
![]()
3. Construct ΔXYZ if XY = 4 cm, ∠X = 45° and ∠Z = 60°.
[Hint : ∠Y = 180° – 45° – 60° = 75°]
Solution:
One side of ΔXYZ as
XY = 4 cm,
∠X = 45°
and ∠Z = 60°.
As we know that by angle-sum property of a triangle; sum of all three angles of a triangle is equal to 180°.
∴ ∠X + ∠Y + ∠Z = 180°
⇒ 45° + ∠Y + 60° = 180°
⇒ 105° + ∠Y = 180°
⇒ ∠Y = 75°.
Now it will be easy to construct triangle with side
XY = 4 cm,
∠X = 45°
and ∠Y = 75°.
Steps of Construction :
Step 1. We first draw a rough sketch of ΔXYZ and indicate the measure of side and two angles.
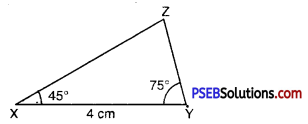
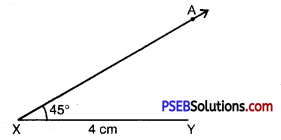
Step 2. Draw a ray XY of length 4 cm.
![]()
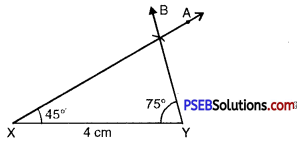
Step 3. At X draw a ray XA making an angle of 45° with XY.
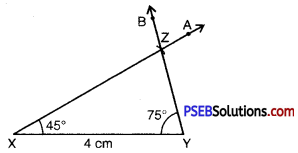
Step 4. At Y; draw a ray YB making an angle of 75° with XY.
Step 5. Z has to lie on both rays XA and YB. So, the point of intersection of two rays is Z.
ΔXYZ is now obtained.
![]()
4. Examine whether you can construct ΔPQR such that ∠P = 100°, ∠Q = 90° and PQ = 4.3 cm If not possible given reason.
Solution:
No, we cannot construct given ΔPQR.
Reason :
As we know that by angle sum property of a triangle; sum of all three angles a triangle is equal to 180°. But in given question sum of two angles;
m∠P + m∠Q
= 100° + 90°
= 190°
The sum of these two angles should be less than 180°. So triangle with given measures cannot be constructed as it violates the angle sum property of a triangle.
5. Question (i).
In which of the following cases a unique triangle can be drawn ?
(a) BC = 5 cm, ∠B = 90° and ∠C = 100°
(b) AB = 4 cm, BC = 7 cm and CA = 2 cm
(c) XY = 5 cm, ∠X = 45°, ∠Y = 60°
(d) An isosceles triangle with length of each equal side equal to 5 cm.
Answer:
(c) XY = 5 cm, ∠X = 45°, ∠Y = 60°
Question (ii).
A triangle can be constructed by taking two of its angles as.
(a) 110°, 40°
(b) 70°, 115°
(c) 135°, 45°
(d) 90°, 90°
Answer:
(a) 110°, 40°
