Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 5 ਰੇਖਾਵਾਂ ਅਤੇ ਕੋਣ Ex 5.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 5 ਰੇਖਾਵਾਂ ਅਤੇ ਕੋਣ Exercise 5.1
1. ਹੇਠਾਂ ਦਿੱਤੇ ਕੋਣਾਂ ਵਿੱਚ ਨਿਊਨ ਕੋਣ, ਅਧਿਕ ਕੋਣ, ਸਮਕੋਣ ਜਾਂ ਰਿਫਲੈਕਸ ਕੋਣ ਦੱਸੋ !
ਪ੍ਰਸ਼ਨ (i)
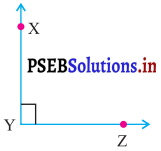
ਉੱਤਰ:
ਸਮਕੋਣ
ਪ੍ਰਸ਼ਨ (ii)
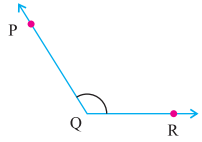
ਉੱਤਰ:
ਅਧਿਕ ਕੋਣ
ਪ੍ਰਸ਼ਨ (iii)
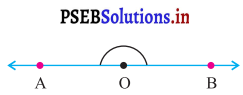
ਉੱਤਰ:
ਸਰਲ ਕੋਣ
![]()
ਪ੍ਰਸ਼ਨ (iv)
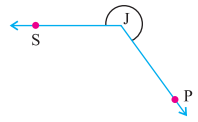
ਉੱਤਰ:
ਰਿਫਲੈਕਸ ਕੋਣ
ਪ੍ਰਸ਼ਨ (v)
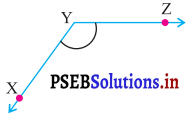
ਉੱਤਰ:
ਅਧਿਕ ਕੋਣ
ਪ੍ਰਸ਼ਨ (vi)
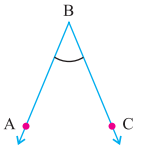
ਉੱਤਰ:
ਨਿਊਨ ਕੋਣ
![]()
2. ਹੇਠਾਂ ਦਿੱਤੇ ਕੋਣਾਂ ਦੇ ਪੂਰਕ ਕੋਣ ਪਤਾ ਕਰੋ ।
ਪ੍ਰਸ਼ਨ (i)
53°
ਉੱਤਰ:
53° ਦਾ ਪੂਰਕ ਕੋਣ
= (90° – 53°) = 37°.
ਪ੍ਰਸ਼ਨ (ii).
90°
ਉੱਤਰ:
90° ਦਾ ਪੂਰਕ ਕੋਣ
= (90° – 90°) = 0°.
ਪ੍ਰਸ਼ਨ (iii).
85°
ਉੱਤਰ:
85° ਦਾ ਪੂਰਕ ਕੋਣ
= (90° – 85°) = 5°.
![]()
ਪ੍ਰਸ਼ਨ (iv).
ਸਮਕੋਣ ਦਾ \(\frac{4}{9}\)
ਉੱਤਰ:
ਸਮਕੋਣ ਦੇ \(\frac{4}{9}\) ਦਾ ਪੂਰਕ
ਇਸ ਲਈ 40° ਦਾ ਪੂਰਕ ਕੋਣ = (90° – 40°) = 50°
[∵ ਸਮਕੋਣ ਦਾ \(\frac{4}{9}\)
= \(\frac{4}{9}\) × 90° = 40°]
ਪ੍ਰਸ਼ਨ (v).
0°
ਉੱਤਰ:
0° ਦਾ ਪੁਰਕ ਕੋਣ = (90° – 0°) = 99°.
3. ਹੇਠਾਂ ਦਿੱਤੇ ਕੋਣਾਂ ਦੇ ਸੰਪੂਰਕ ਕੋਣ ਪਤਾ ਕਰੋ !
ਪ੍ਰਸ਼ਨ (i).
55°
ਉੱਤਰ:
55° ਦਾ ਸੰਪੂਰਕ ਕੋਣ
= (180° – 55°) = 125°.
![]()
ਪ੍ਰਸ਼ਨ (ii).
105°
ਉੱਤਰ:
105° ਦਾ ਸੰਪੂਰਕ ਕੋਣ
= (180° – 105°) = 75°.
ਪ੍ਰਸ਼ਨ (iii).
100°
ਉੱਤਰ:
100° ਦਾ ਸੰਪੂਰਕ ਕੋਣ
= (180° – 100°) = 80°.
ਪ੍ਰਸ਼ਨ (iv).
ਸਮਕੋਣ ਦਾ \(\frac{2}{3}\)
ਉੱਤਰ:
ਸਮਕੋਣ ਦਾ \(\frac{2}{3}\)
= \(\frac{2}{3}\) × 90° = 60.
∴ 60° ਦਾ ਸੰਪੂਰਕ ਕੋਣ
= ( 180° – 60°) = 120°.
![]()
ਪ੍ਰਸ਼ਨ (v).
270° ਦਾ \(\frac{1}{3}\)
ਉੱਤਰ:
270 ਦਾ \(\frac{1}{3}\) = \(\frac{1}{3}\) × 270° = 90°
ਇਸ ਲਈ 90° ਦਾ ਸੰਪੂਰਕ ਕੋਣ – ( 180° – 90°) = 90°
4. ਹੇਠਾਂ ਦਿੱਤੇ ਕੋਣਾਂ ਦੇ ਜੋੜਿਆਂ ਵਿੱਚੋਂ ਪੂਰਕ ਕੋਣਾਂ ਦੇ ਜੋੜੇ ਜਾਂ ਸੰਪੂਰਕ ਕੋਣਾਂ ਦੇ ਜੋੜੇ ਦੱਸੋ :
ਪ੍ਰਸ਼ਨ (i).
65° ਅਤੇ 15°
ਉੱਤਰ:
ਕਿਉਂਕਿ 65° + 115° = 180°.
∴ ਇਹ ਸੰਪੂਰਕ ਕੋਣਾਂ ਦਾ ਜੋੜਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ (ii).
112° ਅਤੇ 68°
ਉੱਤਰ:
ਕਿਉਂਕਿ 112° + 68° = 180°
∴ ਇਹ ਸੰਪੂਰਕ ਕੋਣਾਂ ਦਾ ਜੋੜਾ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ (iii).
63° ਅਤੇ 27°
ਉੱਤਰ:
ਕਿਉਂਕਿ 63° + 27° = 90°
∴ ਇਹ ਪੂਰਕ ਕੋਣਾਂ ਦਾ ਜੋੜਾ ਹੈ ॥
ਪ੍ਰਸ਼ਨ (iv).
45° ਅਤੇ 45°
ਉੱਤਰ:
ਕਿਉਂਕਿ 45° + 45° = 90°
∴ ਇਹ ਪੂਰਕ ਕੋਣਾਂ ਦਾ ਜੋੜਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ (v).
130° ਅਤੇ 50°
ਉੱਤਰ:
ਕਿਉਂਕਿ 130° + 50° = 180°.
∴ ਇਹ ਸੰਪੂਰਕ ਕੋਣਾਂ ਦਾ ਜੋੜਾ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 5.
ਦੋ ਪੂਰਕ ਕੋਣ 4 : 5 ਵਿਚ ਹਨ, ਕੋਣ ਪਤਾ ਕਰੋ ।
ਹੱਲ :
ਕੋਣਾਂ ਦਾ ਅਨੁਪਾਤ = 4 : 5
ਮੰਨ ਲਓ ਪੂਰਕ ਕੋਣ 4x ਅਤੇ 5x ਹਨ ।
ਇਹਨਾਂ ਦਾ ਜੋੜ = 90°
∴ 4x + 3x = 90°
9x = 90°
x = 10
∴ ਪਹਿਲਾ ਕੋਣ = 4x = 4 × 10° = 40°.
ਦੂਜਾ ਕੋਣ = 5x = 4 × 10° = 50°
ਪ੍ਰਸ਼ਨ 6.
ਦੋ ਸੰਪੂਰਕ ਕੋਣ 5 : 13 ਵਿਚ ਹਨ, ਕੋਣ ਪਤਾ ਕਰੋ ।
ਹੱਲ :
ਸੰਪੂਰਕ ਕੋਣਾਂ ਦਾ ਅਨੁਪਾਤ = 5 : 13
ਮੰਨ ਲਓ 5x ਅਤੇ 13x ਦੋ ਸੰਪੂਰਕ ਕੋਣ ਹਨ
ਇਹਨਾਂ ਦਾ ਜੋੜ = 180°
∴ 5x + 13x = 180°
18x = 180°
x = 10°
∴ ਪਹਿਲਾ ਕੋਣ = 5x = 5 × 10° = 50°.
ਦੂਜਾ ਕੋਣ = 13x = 13 × 10° = 130°
![]()
ਪ੍ਰਸ਼ਨ 7.
ਉਹ ਕੋਣ ਪਤਾ ਕਰੋ ਜੋ ਆਪਣੇ ਪੂਰਕ ਕੋਣ ਦੇ ਬਰਾਬਰ ਹੈ ।
ਹੱਲ :
ਮੰਨ ਲਓ ਇੱਕ ਕੋਣ = x
ਇਸ ਲਈ ਕੋਣ ਦਾ ਪੂਰਕ ਕੋਣ = 90° – x
ਕਿਉਂਕਿ ਕੋਣ ਆਪਣੇ ਪੂਰਕ ਕੋਣ ਦੇ ਸਮਾਨ ਹੈ ।
∴ x = 90° – x
ਜਾਂ x + x = 90°
ਜਾਂ 2x = 90°
ਜਾਂ x = \(\frac{90^{\circ}}{2}\)
ਜਾਂ x = 450
ਇਸ ਲਈ 45° ਲੋੜੀਂਦਾ ਕੋਣ ਹੈ
ਪ੍ਰਸ਼ਨ 8.
ਉਹ ਕੋਣ ਪਤਾ ਕਰੋ ਜੋ ਆਪਣੇ ਸੰਪੂਰਕ ਕੋਣ ਦੇ ਬਰਾਬਰ ਹੈ ।
ਹੱਲ :
ਮੰਨ ਲਓ ਇੱਕ ਕੋਣ x ਹੈ ।
ਇਸਦਾ ਸੰਪੂਰਕ ਕੋਣ = 180° – x
ਕਿਉਂਕਿ ਕੋਣ ਸੰਪੂਰਕ ਦੇ ਬਰਾਬਰ ਹੈ ।
∴ x = 180° – x
ਜਾਂ x + x = 180°
ਜਾਂ 2x = 180°
x = 90°
ਇਸ ਲਈ ਲੋੜੀਂਦਾ ਕੋਣ 90° ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 9.
ਦਿੱਤੇ ਚਿੱਤਰ ਵਿੱਚ, AOB ਇੱਕ ਸਰਲ ਰੇਖਾ ਹੈ, ∠AOC ਦਾ ਮਾਪ ਪਤਾ ਕਰੋ ।
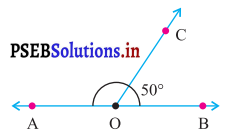
ਹੱਲ :
ਦਿੱਤੇ ਚਿੱਤਰ ਵਿੱਚ AOB ਇਕ ਸਰਲ ਰੇਖਾ ਹੈ ।
∠AOC ਦਾ ਮਾਪ ਪਤਾ ਕਰੋ ।
∴ ∠AOB = 180°
∴ ∠AOC + ∠BOC = 180°
ਜਾਂ ∠AOC + 50° = 180°
[∵ ∠BOC = 50° (ਦਿੱਤਾ ਗਿਆ)]
∴ ∠AOC = 180° – 50°
= 130°
ਪ੍ਰਸ਼ਨ 10.
ਦਿੱਤੇ ਚਿੱਤਰ ਵਿੱਚ, MON ਇੱਕ ਸਰਲ ਰੇਖਾ ਹੈ । ਪਤਾ ਕਰੋ ।
(i) ∠MOP
(ii) ∠NOP
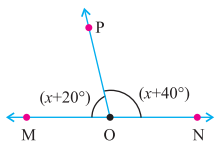
ਹੱਲ :
ਕਿਉਂਕਿ MON ਇਕ ਸਰਲ ਰੇਖਾ ਹੈ ।
∴ ∠MON = 180°
∴ ∠MOP + ∠NOP = 180°
[∵∠MOP = x + 20°
∠NOP = x + 40°]
ਜਾਂ 2x + 60° = 180°
ਜਾਂ 2x = 180° – 60°
ਜਾਂ 2x = 120°
ਜਾਂ x = \(\frac{120^{\circ}}{2}\) = 60°
(i) ∠MOP = x + 20° = 60° + 20° = 80°
(ii) ∠NOP = x + 40° = 60° + 40°
= 100° ਉੱਤਰ
![]()
11. ਤੇ ਚਿੱਤਰਾਂ ਵਿੱਚ x, y ਅਤੇ z ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਪ੍ਰਸ਼ਨ (i).
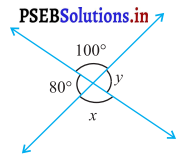
ਉੱਤਰ:
ਪਹਿਲੇ ਚਿੱਤਰ ਵਿੱਚ
x = 100° (ਸਿਖਰ ਸਨਮੁੱਖ ਕੋਣ)
y = 80° ਸਿਖਰ ਸਨਮੁੱਖ ਕੋਣ)
ਪ੍ਰਸ਼ਨ (ii).
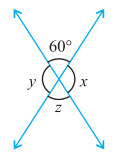
ਉੱਤਰ:
ਦੂਜੇ ਚਿੱਤਰ ਵਿੱਚ
∠ = 60° (ਸਿਖਰ ਸਨਮੁੱਖ ਕੋਣ)
∠y + 60°= 180° (ਰੇਖੀ ਜੋੜਾ)
ਜਾਂ y = 180° – 60° = 120°
x = y (ਸਿਖਰ ਸਨਮੁੱਖ ਕੋਣ)
= 120°
![]()
12. ਦਿੱਤੇ ਚਿੱਤਰਾਂ ਵਿੱਚ x, y, z ਅਤੇ p ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਪ੍ਰਸ਼ਨ (i).
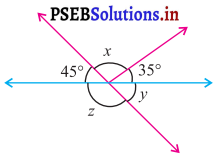
ਉੱਤਰ:
ਪਹਿਲੇ ਚਿੱਤਰ ਵਿੱਚ
45° + x + 35°= 180° (ਰੇਖੀ ਜੋੜਾ)
ਜਾਂ x + 80° = 180°
ਜਾਂ x = 180° – 80°
ਜਾਂ x = 100°
y = 45° (ਸਿਖਰ ਸਨਮੁੱਖ ਕੋਣ)
ਇਸੇ ਤਰ੍ਹਾਂ 45° + ∠ = 180° (ਰੇਖਾ ਜੋੜਾ)
∴ ∠ = 180° – 450
= 135°
ਇਸ ਲਈ = 100°, y = 45°, ∠ = 135°
ਪ੍ਰਸ਼ਨ (ii).
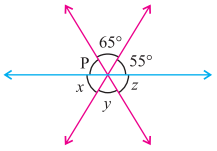
ਉੱਤਰ:
ਚਿੱਤਰ (ii) ਵਿੱਚ
p + 65° + 55° = 180° (ਰੇਖੀ ਜੋੜਾ)
p + 120° = 180°
∴ p = 60°
x = 55° (ਸਿਖਰ ਸਨਮੁੱਖ ਕੋਣ)
∠ = P
y = 60° (ਸਿਖਰ ਸਨਮੁੱਖ ਕੋਣ)
ਇਸ ਲਈ x = 55°, y = 65°, ∠ = 60°,
p = 60°
![]()
13. ਬਹੁਵਿਕਲਪੀ ਪ੍ਰਸ਼ਨ :
ਪ੍ਰਸ਼ਨ (i)
ਜੇਕਰ ਦੋ ਕੋਣ ਪੂਰਕ ਹਨ ਤਾਂ ਉਹਨਾਂ ਦਾ …………. ਹੁੰਦਾ ਹੈ ।
(a) 180°
(b) 90°
(c) 360°
(d) ਇਹਨਾਂ ਵਿਚੋਂ ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ:
(b) 90°
ਪ੍ਰਸ਼ਨ (ii).
ਦੋ ਕੋਣਾਂ ਨੂੰ ………… ਕੋਣ ਕਹਿੰਦੇ ਹਨ, ਜੇਕਰ ਉਹਨਾਂ ਦਾ ਜੋੜ 180° ਹੋਵੇ ।
(a) ਸੰਪੂਰਕ
(b) ਪੂਰਕ
(c) ਸਮਕੋਣ
(d) ਇਹਨਾਂ ਵਿਚੋਂ ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ:
(a) ਸੰਪੂਰਕ
![]()
ਪ੍ਰਸ਼ਨ (iii).
ਜੇਕਰ ਦੋ ਲਾਗਵੇਂ ਕੋਣ ਸੰਪੂਰਕ ਹਨ ਤਾਂ ਉਹ ………….. ਬਣਾਉਂਦੇ ਹਨ ।
(a) ਸਮਕੋਣ
b) ਸਿਖਰ ਸਨਮੁੱਖ ਕੋਣ
(c) ਰੇਖੀ ਜੋੜਾ
(d) ਸੰਗਤ ਕੋਣ ।
ਉੱਤਰ:
(c) ਰੇਖੀ ਜੋੜਾ
ਪ੍ਰਸ਼ਨ (iv).
ਜੇਕਰ ਦੋ ਰੇਖਾਵਾਂ ਇੱਕ ਬਿੰਦੂ ‘ ਤੇ ਕੱਟਦੀਆਂ ਹਨ ਤਾਂ ਸਿਖਰ ਸਨਮੁੱਖ ਕੋਣ ਹਮੇਸ਼ਾ ……… ਹੁੰਦੇ ਹਨ ।
(a) ਬਰਾਬਰ
(b) ਸਿਫਰ
(c) 90°
(d) ਇਹਨਾਂ ਵਿਚੋਂ ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ:
(a) ਬਰਾਬਰ
