Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 6 Triangles Ex 6.3 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 6 Triangles Ex 6.3
1. Find the length of the unknown side in each of following figures
Question (i).
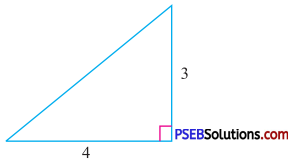
Answer:
Take a = 3 cm, b = 4 cm and unknown side = c
By Pythagoras Theorem
c2 = a2 + b2
c2 = (3)2 + (4)2
c2 = 9 + 16
c2 = 25
∴ c = \(\sqrt{25}\)
c = 5
Thus, the length of unknown side = 5 cm.
Question (ii).
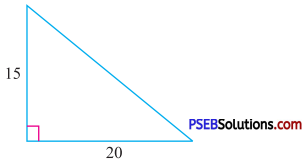
Answer:
Take a = 15 cm, b = 20 cm
By Pythagoras Theorem
c2 = a2 + b2
∴ c2 = (15)2 + (20)2
c2 = 225 + 400
c2 = 625
∴ c = \(\sqrt{625}\)
c = 25
Thus, the length of unknown side = 5 cm
![]()
2. Which of the following can be the sides of a right triangle ?
(i) 4 cm, 5 cm, 7 cm
(ii) 1.5 cm, 2 cm, 2.5 cm
(iii) 2 cm, 2 cm, 5 cm
In the case of right angled triangles, identify the right angles.
Solutions:
(i) Let in ΔABC, the longest side is AB = 7 cm
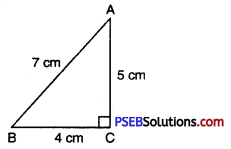
(BC)2 + (AC)2
= (4)2 + (5)2
= 16 + 25 = 41
(BC)2 + (AC)2 = 41
Also AB2 = (7)2 = 49
Since AB2 ≠ (BC)2 + (AC)2
∴ The triangles with the given sides is not a right triangle.
(ii) Let in ΔABC, the longest side is AB = 2.5 cm
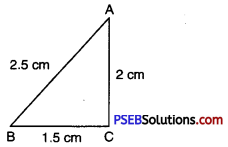
(AB)2 = (2.5)2 = 6.25 ….(1)
(BC)2 + (AC)2
= (1.5)2 + (2)2
= 2.25 + 4
= 6.25
∴ (BC)2 + (AC)2 = 6.25 ….(2)
From (1) and (2)
(AB)2 = (BC)2 + (AC)2
Therefore, the given triangle is a right triangle.
The angle opposite to the longest side is right angle.
(iii) Let in ΔABC, the longest side is AB = 5 cm
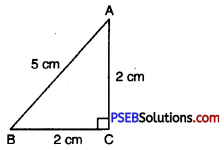
(AB)2 = (5)2
(AB)2 = 25 ….(1)
(BC)2 + (AC)2 = (2)2 + (2)2
(BC)2 + (AC)2 = 4 + 4
(BC)2 + (AC)2 = 8 …..(2)
From (1) and (2)
(AB)2 ≠ (BC)2 + (AC)2
Therefore the triangle whose sides are 5 cm, 2 cm and 2 cm is not a right triangle.
![]()
3. Find the area and the perimeter of the rectangle whose length is 15 cm and the length of one diagonal is 17 cm.
Solution:
Let ABCD be a rectangle with length AB = 15 cm and diagonal AC = 17 cm.
In ΔABC, ∠B = 90° (Each angle of a rectangle)
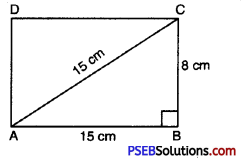
By Pythagoras Theorem,
(AC)2 = (AB)2 + (BC)2
(17)2 = (15)2 + (BC)2
289 = 225 + (BC)2
(BC)2 = 289 – 225 = 64
BC = 8 cm
Area of rectangle ABCD
= AB × BC
= 15 cm × 8 cm
= 120 cm2
Perimeter of rectangle ABCD = 2(AB + BC)
= 2(15 cm + 8 cm)
= 2(23 cm) = 46 cm2
4. A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance, find the distance of the foot of the ladder from the wall.

Solution:
Let AB be the ladder and BC be the distance of the foot of the ladder from the wall then AB = 15 m and AC = 12 m
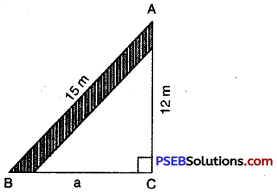
By Pythagoras Theorem,
AB2 = BC2 + AC2
(15)2 = BC2 + (12)2
225 = BC2 + 144
BC2 = 225 – 144
BC2 = 81
BC =9
Hence the distance of the foot of the ladder from the wall is 9 m.
![]()
5. The side of a rhombus is 5 cm. If the length of one of the diagonals of the rhombus is 8 cm, then find the length of the other diagonal.
Solution:
Let ABCD be a rhombus with side AB = 5 cm and diagonal AC = 8 cm
Let diagonal AC and BD bisect each other at O.
Then OA = OC = \(\frac {8}{2}\) cm = 4 cm
The diagonals of a rhombus bisect each other at right angle
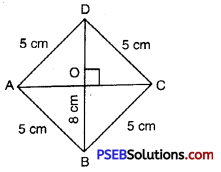
∴ In right angled ΔAOB,
AO = 4 cm, AB = 5 cm
By Pythagoras Theorem,
OA2 + OB2 = AB2
(4)2 + OB2 = (5)2
16 + OB2 = 25
OB2 = 25 – 16 = 9
OB = 3 cm
Diagonal BD = 2 × OB = 2 × 3cm = 6cm
Therefore other diagonal of rhombus = 6 cm.
6. A right triangle is isosceles. If the square of the hypotenuse is 50 m, what is length of each of its sides ?
Solution:
Let ΔABC is a right isosceles triangle in which (AC)2 = 50 m and AB = AC
∴ By Pythagoras Theorem
AB2 + BC2 = AC2
∴ AB2 + AB2 = AC2
2AB2 = 50
AB2 = 25
AB = 5
Therefore length of each equal side = 5m.
7. ΔABC is a triangle right angled at C if AC = 8 cm and BC = 6 cm, find AB.
Solution:
In right angled triangle ABC right angle at C
AC = 8 cm and BC = 6 cm
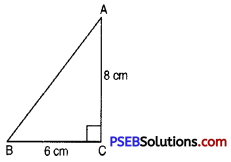
By Pythagoras Theorem
AB2 = AC2 + BC2
AB2 = (8)2 + (6)2
AB2 = 100
AB = 10 cm.
![]()
8. State whether the following triplets are Pythagorean or not.
Question (i).
(5, 7, 12)
Solution:
Let a = 5, b = 1, c = 12
∴ c2 = (12)2 = 144
a2 + b2 = (5)2 + (7)2
= 25 + 49 = 74
∴ a2 + b2 ≠ c2
∴ (5, 7, 12) is not a pythagorean triplet.
Question (ii).
(3, 4, 5)
Solution:
Let a = 3, b = 4, c = 5
∴ a2 + b2 = (3)2 + (4)2
= 9 + 16 = 25
c2 = (5)2 = 25
∴ c2 = a2 + b2
∴ (3, 4, 5) is a pythagorean triplet
Question (iii).
(8, 9, 10)
Solution:
Let a = 8, b = 9, c = 10
∴ a2 + b2 = (8)2 + (9)2
= 64 + 81 = 145
c2 = (10)2 = 100
c2 ≠ a2 + b2
Therefore (8, 9, 10) is not a pythagorean triplet.
Question (iv).
(5, 12, 13)
Solution:
Let a = 5, b = 12, c = 13
∴ a2 + b2 = (5)2 + (12)2
= 25 + 144 = 169
c2 = (13)2 = 169
a2 + b2 ≠ c2
Therefore (5, 12, 13) is a pythagorean triplet.
![]()
9. Multiple Choice Questions :
Question (i).
In a ΔABC, if ∠A = 40° and ∠B = 55° then ∠C is
(a) 75°
(b) 80°
(c) 95°
(d) 85°
Answer:
(d) 85°
Question (ii).
If the angles of a triangle are 35°, 35° and 110°, then it is
(a) an isosceles triangle
(b) an equilateral triangle
(c) a scalene triangle
(d) right angled triangle
Answer:
(a) an isosceles triangle
Question (iii).
A triangle can have two
(a) right angles
(b) obtuse angles
(c) acute angles
(d) straight angles
Answer:
(c) acute angles
Question (iv).
A triangle whose angles measure 35°, 55° and 90° is
(a) acute angled
(b) right angled
(c) obtuse angled
(d) isosceles
Answer:
(b) right angled
![]()
Question (v).
A triangle is not possible whose angles measure
(a) 40°, 65°, 75°
(b) 50°, 56°, 74°
(c) 72°, 63°, 45°
(d) 67°, 42°, 81°
Answer:
(d) 67°, 42°, 81°
Question (vi).
A triangle is not possible with sides of lengths (in cm)
(a) 6, 4, 10
(b) 5, 3, 7
(c) 7, 8, 9
(d) 3.6, 5.4, 8
Answer:
(a) 6, 4, 10
Question (vii).
In a right angled triangle, the length of two legs are 6 cm and 8 cm. The length of the hypotenuse is
(a) 14 cm
(b) 10 cm
(c) 11 cm
(d) 12 cm
Answer:
(b) 10 cm
