PSEB 8th Class Maths Solutions Chapter 12 ਘਾਤ ਅੰਕ ਅਤੇ ਘਾਤ Ex 12.1

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 12 ਘਾਤ ਅੰਕ ਅਤੇ ਘਾਤ Ex 12.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 12 ਘਾਤ ਅੰਕ ਅਤੇ ਘਾਤ Exercise 12.1

1. ਮੁੱਲ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
3^-2
ਹੱਲ:
3^-2
⇒ 3^-2 = \(\frac{1}{3^{2}}\) = \(\frac{1}{3×3}\) = \(\frac{1}{9}\)

ਪ੍ਰਸ਼ਨ (ii).
(-4)^-2
ਹੱਲ:
(-4)^-2
⇒ (-4)^-2 = \(\frac{1}{(-4)^{2}}\) = \(\frac{1}{(-4)×(-4)}\) = \(\frac{1}{16}\)

ਪ੍ਰਸ਼ਨ (iii).
(\(\frac{1}{2}\))^-5
ਹੱਲ:
(\(\frac{1}{2}\))^-5
⇒ (\(\frac{1}{2}\))^-5 = \(\frac{(1)^{-5}}{(2)^{-5}}\)
= \(\frac{1}{(1)^{5}}\) × \(\frac{(2)^{5}}{1}\) = \(\frac{2^{5}}{1}\) = 2²
= 2 × 2 × 2 × 2 × 2
= 32

2. ਸਰਲ ਕਰੋ ਅਤੇ ਉੱਤਰ ਨੂੰ ਧਨਾਤਮਕ ਘਾਤ ਅੰਕਾਂ ਤੇ ਰੂਪ ਵਿਚ ਦਰਸਾਓ ।

ਪ੍ਰਸ਼ਨ (i).
(-4)⁵ ÷ (-4)⁸
ਹੱਲ:
(-4)⁵ ÷ (-4)⁸
[∵ a^m ÷ aⁿ = a^m-n]
⇒ (-4)⁵ ÷ (-4)⁸ = (-4)^5-8
= (-4)^-3
= \(\frac{1}{(-4)^{3}}\)

ਪ੍ਰਸ਼ਨ (ii).
(\(\frac{1}{2^{3}}\))²
ਹੱਲ:
(\(\frac{1}{2^{3}}\))²
⇒ (\(\frac{1}{2^{3}}\))² = \(\frac{1^{2}}{\left(2^{3}\right)^{2}}\) = \(\frac{1}{2^{6}}\) [∵(a^m)ⁿ = a^mn]

ਪ੍ਰਸ਼ਨ (iii).
(-3)⁴ × (\(\frac{5}{3}\))⁴
ਹੱਲ:
(-3)⁴ × (\(\frac{5}{3}\))⁴
⇒ (-3)⁴ × (\(\frac{5}{3}\))⁴ = (-3) × (-3) × (-3) × (-3) × \(\frac{(5)^{4}}{(3)^{4}}\)
= 81 × \(\frac{5^{4}}{3 \times 3 \times 3 \times 3}\)
= 5⁴

ਪ੍ਰਸ਼ਨ (iv).
(3^-7 ÷ 3^-10) × 3^-5
ਹੱਲ:
(3^-7 ÷ 3^-10) × 3^-5
⇒ (3^-7 ÷ 3^-10) × 3^-5
= (3^-7-(-10)) × 3^-5 [a^m ÷ aⁿ = a^m-n]
= 3^-7+10 × 3^-5
= 3³ × 3^-5 [a^m × aⁿ = a^m+n]
= 3^3+(-5) = 3^3-5 = 3^-2 = \(\frac{1}{3^{2}}\)

ਪ੍ਰਸ਼ਨ (v).
2^-3 × (-7)^-3
ਹੱਲ:
2^-3 × (-7)^-3 = [2 × (-7)]^-3] = [-14]^-3.
= \(\frac{1}{[-14]^{3}}\)

3. ਮੁੱਲ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
(3⁰ + 4^-1) × 2²
ਹੱਲ:
(3⁰ + 4^-1) × 2²
∴ (3⁰ + 4^-1) × 2² = (1 +\(\frac{1}{4}\)) × 4
= (\(\frac{4+1}{4}\)) × 4 = 5

ਪ੍ਰਸ਼ਨ (ii).
(2^-1 × 4^-1) ÷ 2^-2
ਹੱਲ:
(2^-1 × 4^-1) ÷ 2^-2
∴ (2^-1 × 4^-1) ÷ 2^-2 = (\(\frac{1}{2}\) × \(\frac{1}{2}\)) ÷ (\(\left(\frac{1}{2^{2}}\right)\))
= \(\frac{1}{8}\) ÷ \(\frac{1}{4}\)
= \(\frac{1}{8}\) × \(\frac{1}{4}\) = \(\frac{1}{2}\)

ਪ੍ਰਸ਼ਨ (iii).
\(\left(\frac{1}{2}\right)^{-2}\) + \(\left(\frac{1}{3}\right)^{-2}\) + \(\left(\frac{1}{4}\right)^{-2}\)
ਹੱਲ:
\(\left(\frac{1}{2}\right)^{-2}\) + \(\left(\frac{1}{3}\right)^{-2}\) + \(\left(\frac{1}{4}\right)^{-2}\)
∴ \(\left(\frac{1}{2}\right)^{-2}\) + \(\left(\frac{1}{3}\right)^{-2}\) + \(\left(\frac{1}{4}\right)^{-2}\)
= \(\frac{1^{-2}}{2^{-2}}\) + \(\frac{1^{-2}}{3^{-2}}\) + \(\frac{1^{-2}}{4^{-2}}\)
= 2² + 3² + 4²
= 4 + 9 + 16
= 29.

ਪ੍ਰਸ਼ਨ (iv).
(3^-1 + 4^-1 + 5^-1)⁰
ਹੱਲ:
(3^-1 + 4^-1 + 5^-1)⁰
∴ (3^-1 + 4^-1 + 5^-1)⁰ = (\(\frac{1}{3}\) + \(\frac{1}{4}\) + \(\frac{1}{5}\))⁰
= (\(\frac{20+15+12}{60}\))⁰
= (\(\frac{47}{60}\))⁰ = 1

ਪ੍ਰਸ਼ਨ (v).
\(\left\{\left(\frac{-2}{3}\right)^{-2}\right\}^{2}\)
ਹੱਲ:

4. ਮੁੱਲ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
\(\frac{8^{-1} \times 5^{3}}{2^{-4}}\)
ਹੱਲ:
ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੈ : \(\frac{8^{-1} \times 5^{3}}{2^{-4}}\)
= \(\frac{1}{8}\) × 5 × 5 × 5 × 2⁴
= \(\frac{125 \times 2 \times 2 \times 2 \times 2}{8}\)
= 250

ਪ੍ਰਸ਼ਨ (ii).
(5^-1 × 2^-1) × 6^-1
ਹੱਲ:
(5^-1 × 2^-1) × 6^-1 = (\(\frac{1}{5}\) × \(\frac{1}{5}\)) × \(\frac{1}{6}\)
= (\(\frac{1}{10}\)) × \(\frac{1}{6}\) = \(\frac{1}{60}\)

ਪ੍ਰਸ਼ਨ 5.
m ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ਜਿਸਦੇ ਲਈ : 5^m ÷ 5^-3 = 5⁵
ਹੱਲ:
ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੈ .
5^m ÷ 5^-3 = 5⁵
⇒ 5^m-(-3) = 5⁵
[∵ a^m ÷ aⁿ = a^m-n]
⇒ 5^m+3 = 5⁵
⇒ m + 3 = 5
⇒ m = 5 – 3
⇒ m = 2.

6. ਮੁੱਲ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
\(\left\{\left(\frac{1}{3}\right)^{-1}-\left(\frac{1}{4}\right)^{-1}\right\}^{-1}\)
ਹੱਲ:
ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੈ :
\(\left\{\left(\frac{1}{3}\right)^{-1}-\left(\frac{1}{4}\right)^{-1}\right\}^{-1}\) = (3 – 4)^-1
= (-1)^-1 = \(\frac{1}{-1}\) = -1

ਪ੍ਰਸ਼ਨ (ii).
\(\left(\frac{5}{8}\right)^{-7}\) × \(\left(\frac{8}{5}\right)^{-4}\)
ਹੱਲ:
\(\left(\frac{5}{8}\right)^{-7}\) × \(\left(\frac{8}{5}\right)^{-4}\)
= \(\left(\frac{8}{5}\right)^{7}\) × \(\left(\frac{5}{8}\right)^{4}\)
= \(\frac{8^{7}}{5^{7}}\) × \(\frac{5^{4}}{8^{4}}\)
= 8^7-4 × 5^9-7
= 8³ × 5^-3
= 8³ × \(\frac{1}{5^{3}}\)
= (\(\frac{8}{5}\))³
= \(\frac{512}{125}\)

7. ਸਰਲ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
\(\frac{25 \times t^{-4}}{5^{-3} \times 10 \times t^{-8}}\) (t ≠ 0)
ਹੱਲ:
ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੈ : \(\frac{25 \times t^{-4}}{5^{-3} \times 10 \times t^{-8}}\)

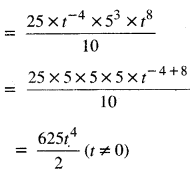
ਪ੍ਰਸ਼ਨ (ii).
\(\frac{3^{-5} \times 10^{-5} \times 125}{5^{-7} \times 6^{-5}}\)
ਹੱਲ:
ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੈ :
\(\frac{3^{-5} \times 10^{-5} \times 125}{5^{-7} \times 6^{-5}}\) = \(\frac{3^{-5} \times(2 \times 5)^{-5} \times 125}{5^{-7} \times(2 \times 3)^{-5}}\)
= \(\frac{3^{-5} \times 2^{-5} \times 5^{-5} \times 125}{5^{-7} \times 2^{-5} \times 3^{-5}}\)
= 3^-5+5 × 2^-5+5 × 5^-5+7 × 125
= 3⁰ × 2⁰ × 5² × 125
= 1 × 1 × 25 × 125
= 3125.