PSEB 9th Class Maths MCQ Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल MCQ Questions with Answers.

PSEB Solutions for Class 9 Maths Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल MCQ Questions

बहुविकल्पीय प्रश्न

दिये गए चार विकल्पों में से सही उत्तर का चयन करें।

प्रश्न 1.
दी गई आकृति में ABCD एक समांतर चतुर्भुज है। लंब AE की लंबाई क्या है ?

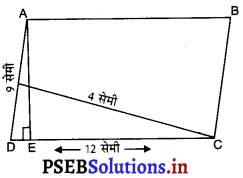
(A) 3 सेमी०
(B) 6 सेमी०
(C) 9 सेमी०
(D) 2 सेमी०।
उत्तर –
(A) 3 सेमी०

प्रश्न 2.
E, F, G और H समांतर चतुर्भुज ABCD की भुजाओं के मध्य बिंदु है।
तब क्षे० (EFGH) = ………. :

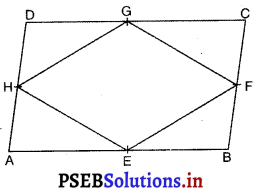
(A) \(\frac {1}{3}\) से (ABCD)
(B) क्षे० (ABCD)
(C) \(\frac {1}{2}\)क्षे० (ABCD)
(D) \(\frac {1}{4}\)क्षे० (ABCD).
उत्तर –
(C) \(\frac {1}{2}\)क्षे० (ABCD)

प्रश्न 3.
दी गई आकृति में ABCD एक समांतर चतुर्भुज है। ABE एक त्रिभुज है। यदि AB || CE हो और क्षे० (ABCD) = 60 सेमी०² हो तो ΔABE का क्षेत्रफल क्या है ?

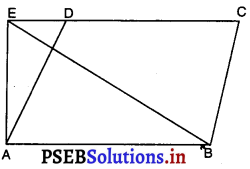
(A) 60 सेमी²
(B) 30 सेमी०²
(C) 120 सेमी०²
(D) 50 सेमी०² ।
उत्तर –
(B) 30 सेमी०²

प्रश्न 4.
ΔABC की माध्यिका AD पर बिंदु E है। यदि क्षे० (ΔABE) = 10 सेमी०² तब क्षे० (ΔACE) है :

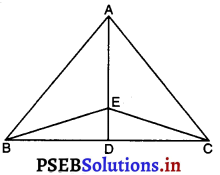
(A) 20 सेमी०²
(B) 5 सेमी०²
(C) 30 सेमी०²
(D) 10 सेमी०²
उत्तर –
(D) 10 सेमी०²

प्रश्न 5.
समलंब चतुर्भुज ABCD में AB || DC है। यदि क्षे० (AOD) = 15 सेमी०² तब क्षे० (BOC) है :
(A) 30 सेमी०²
(B) 15 सेमी०²
(C) 10 सेमी०²
(D) 7.5 सेमी.² ।

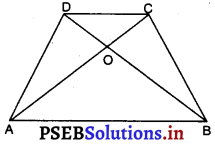
उत्तर –
(B) 15 सेमी०²

प्रश्न 6.
एक त्रिभुज की माध्यिका उसे विभाजित करती है,
(A) बराबर क्षेत्रफल वाले त्रिभुजों में
(B) सर्वांगसम त्रिभुजों में
(C) समकोण त्रिभुजों में
(D) समद्विबाहु त्रिभुजों में
उत्तर –
(A) बराबर क्षेत्रफल वाले त्रिभुजों में

प्रश्न 7.
निम्नलिखित आकृतियों में से किसमें आप एक ही आधार पर और एक ही समांतर रेखाओं के बीच, बने दो बहुभुज प्राप्त होते हैं :

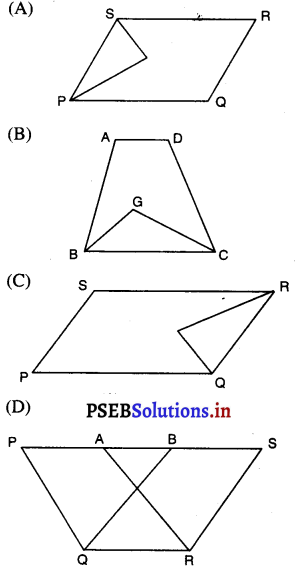
उत्तर –

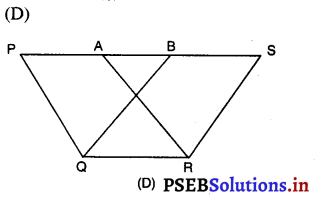
प्रश्न 8.
8cm और 6 cm भुजाओं वाले एक आयत की आसन्न भुजाओं के मध्य-बिन्दुओं को मिलाने से बनी आकृति है :
(A) 24 cm² क्षेत्रफल का एक आयात
(B) 25 cm² क्षेत्रफल का एक वर्ग
(C) 24 cm² क्षेत्रफल का एक समलंब
(D) 24 cm² क्षेत्रफल का एक समचतुर्भुज
उत्तर –
(D) 24 cm² क्षेत्रफल का एक समचतुर्भुज

प्रश्न 9.
आकृति में, समांतर चतुर्भुज ABCD का क्षेत्रफल हैं :
(A) AB × BM
(B) BC × BN
(C) DC × DL
(D) AD × DL

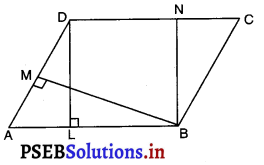
उत्तर –
(C) DC × DL

प्रश्न 10.
आकृति में, यदि समांतर चतुर्भुज ABCD और आयत AREM समान क्षेत्रफल के हैं, तो :
(A) ABCD का परिमाप = ABEM का परिमाप
(B) ABCD का परिमाप < AREM का परिमाप
(C) ABCD का परिमाप > ABEM का परिमाप
(D) ABCD का परिमाप = \(\frac {1}{2}\)(ABEM का परिमाप)

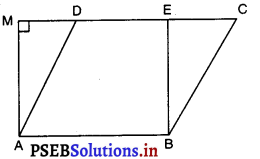
उत्तर –
(C) ABCD का परिमाप > ABEM का परिमाप

प्रश्न 11.
एक त्रिभुज की भुजाओं के मध्य बिंदु किसी भी एक शीर्ष को चौथा बिंदु लेकर एक समांतर चतुर्भुज बनाते हैं, जिसका क्षेत्रफल बराबर है :
(A) \(\frac {1}{2}\)ar (ABC)
(B) \(\frac {1}{3}\)ar (ABC)
(C) \(\frac {1}{4}\)ar (ABC)
(D) ar (ABC)
उत्तर –
(A) \(\frac {1}{2}\)ar (ABC)

प्रश्न 12.
दो समांतर चतुर्भुज बराबर आधारों पर और एक ही समांतर रेखाओं के बीच स्थित हैं। उनके क्षेत्रफलों का अनुपात है।
(A) 1 : 2
(B) 1 : 1
(C) 2 : 1
(D) 3 : 1.
उत्तर –
(B) 1 : 1

प्रश्न 13.
ABCD एक चतुर्भुज है जिसका विकर्ण AC उसे बराबर क्षेत्रफल वाले दो भागों में विभाजित करता है। तब, ABCD
(A) एक आयत है
(B) सदैव एक समचतुर्भुज है
(C) एक समांतर चतुर्भुज है।
(D) (A), (B) या (C) में से कोई भी होना आवश्यक नहीं।
उत्तर –
(D) (A), (B) या (C) में से कोई भी होना आवश्यक नहीं।

प्रश्न 14.
एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार पर और एक ही समांतर रेखाओं के बीच स्थित हैं, तो त्रिभुज के क्षेत्रफल का समांतर चतुर्भुज के क्षेत्रफल से अनुपात है।
(A) 1 : 3
(B) 1 : 2
(C) 3 : 1
(D) 1 : 4
उत्तर –
(B) 1 : 2

प्रश्न 15.
ABCD एक समलंब है जिसकी समांतर भुजाएँ AB = a cm और DC = bcm है। E और F असमांतर भुजाओं के मध्य-बिंदु हैं। ar (ABFE) और ar (EFCD) का अनुपात है।
(A) ab
(B) (3a + b) : (a + 3b)
(C) (a + 3b) : (3a + 3b)
(D) (2a + b) : (3a + b)

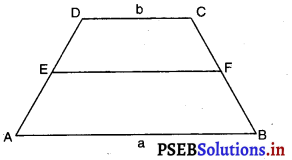
उत्तर –
(B) (3a + b) : (a + 3b)