Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 1 संख्या पद्धति Ex 1.3 Textbook Exercise Questions and Answers
PSEB Solutions for Class 9 Maths Chapter 1 संख्या पद्धति Ex 1.3
प्रश्न 1.
निम्नलिखित भिन्नों को दशमलव रूप में लिखिए और बताइए कि प्रत्येक का दशमलव प्रसार किस प्रकार का है :
(i) \(\frac{36}{100}\)
(ii) \(\frac{1}{11}\)
(iii) 4 \(\frac{1}{8}\)
(iv) \(\frac{3}{13}\)
(v) \(\frac{2}{11}\)
(vi) \(\frac{329}{400}\)
हल:
(i) \(\frac{36}{100}\) = 0.36 सांत दशमलव
(ii) \(\frac{1}{11}\)

शेष : 1, 1, 1, 1……………..
भाजक : 11
हम लिखते हैं \(\frac{1}{11}\) = 0.09090909……..
= \(0 . \overline{09}\) अनवसानी पुनरावर्ती
![]()
(iii) 4 \(\frac{1}{8}\) = \(\frac{33}{8}\)

शेष : 1, 2, 4, 0
भाजक : 8
हम लिखते हैं 4 \(\frac{1}{8}\) = \(\frac{33}{8}\) = 4.125 सांत दशमलव
(iv) \(\frac{3}{13}\)

शेष : 4, 1, 9, 12, 3, 4, 1, 9, 12, 3….
भाजक : 13
हम लिखते हैं :
\(\frac{3}{13}\) = 0.230769230769 = \(0 . \overline{230769}\) अनवसानी पुनरावर्ती

(v) \(\frac{2}{11}\)

शेष : 9, 2, 9, 2 ………..
भाजक : 0.1818 …………..
हम लिखते हैं :
\(\frac{2}{11}\) = 0.1818 … 11
= \(0 . \overline{18}\) अनवसानी पुनरावर्ती
(vi) \(\frac{329}{400}\)
= \(\frac{329}{100 \times 4}\)
= \(\frac{82.25}{100}\)
= 0.8225 सांत


प्रश्न 2.
आप जानते हैं कि \(\frac{1}{7}\) = 0.142857 है। वास्तव में, लंबा भाग दिए बिना क्या आप यह बता सकते हैं कि \(\frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7}\) के दशमलव प्रसार क्या हैं ? यदि हाँ, तो कैसे ?
हल :
हाँ, उपरोक्त सभी का प्रसार आवर्ती दशमलव है जो कि 1, 4, 2, 8, 5, 7. का प्रस्तार है।
उदाहरण के लिए, यहाँ \(\frac{1}{7}\) है।

\(\frac{1}{7}\) = 0.142857
\(\frac{2}{7}\) को ज्ञात करने के लिए, पता लगाइए कब शेष 2 आता है, और उससे संबंधित भागफल (यहाँ पर 2 है) तब वहाँ से आरंभ होने वाला नया भागफल लिखिए। (उपरोक्त आकृति में पुनरावृत्ति अंकों 1, 4, 2, 8, 5, 7 के ऊपर दंड लगाया गया है।
अतः \(\frac{2}{7}\) = 0.285714.
![]()
प्रश्न 3.
निम्नलिखित को \(\frac{p}{q}\) के रूप में व्यक्त कीजिए, जहाँ p और q पूर्णांक हैं तथा q # 0 है :
(i) \(0 . \overline{6}\)
(ii) \(0.4 \overline{7}\)
(iii) \(0 . \overline{001}\)
हल :
(i) क्योंकि हम यह नहीं जानते कि \(0 . \overline{6}\) क्या है, अतः आइए इसे हम ‘x’मान लें।
x = 0.6666…………(1)
दोनों ओर 10 से गुणा करने पर, हमें प्राप्त होता है :
10x = 10 × .6666 ………………..
⇒ 10x = 6.6666 ……………(2)
(1) को (2) में से घटाने पर, हमें प्राप्त होता है :
10x – x = (6.6666………) – (.6666………)
⇒ 9x = 6
⇒ x = \(\frac{6}{9}\)
⇒ x = \(\frac{2}{3}\) ………….. (1)

(ii) मान लीजिए x = 0.47
x = 0.4777 ……………(1)
दोनों ओर 10 से गुणा करने पर, हमें प्राप्त होता है :
10x = 4.7777………….(2)
(1) को (2) में से घटाने पर, हमें प्राप्त होता है :
10x – x = (4.7777……..) – (0.4777………..)
⇒ 9x = 4.3
⇒ x = \(\frac{4.3}{9}\)
x = \(\frac{43}{90}\)
(iii) मान लीजिए x = \(0 . \overline{001}\)
x = 0.001001001 ………….. (1)
दोनों ओर 1000 से गुणा करने पर, हमें प्राप्त होता है :
1000x = 1.001001 ……………(2)
(1) को (2) में से घटाने पर, हमें प्राप्त होता है :
1000x – x = (1.001001………) – (0.001001……..)
⇒ 999x = 1
⇒ x = \(\frac{1}{999}\)
प्रश्न 4.
0.99999 ……………….. को \(\frac{p}{q}\) के रूप में व्यक्त कीजिए। क्या आप अपने उत्तर से आश्चर्यचकित हैं ? अपने अध्यापक और कक्षा के सहयोगियों के साथ उत्तर की सार्थकता पर चर्चा कीजिए।
हल :
मान लीजिए x = 0.99999 …………………..(1)
दोनों ओर 10 से गुणा करने पर, हमें प्राप्त होता है
10x = 9.9999 ………………. (2)
(1) को (2) घटाने पर हमें प्राप्त होता है :
10x – x = (9.9999………) – (0.9999…….)
⇒ 9x = 9
⇒ x = \(\frac{9}{9}\)
⇒ x = 1
हाँ, अपने उत्तर से हम आश्चर्यचकित हैं।
परंतु उत्तर सार्थक होता है जब हम देखते हैं कि 0.9999………… सदा चलता रहता है।
इस प्रकार 1 और 0.9999……… के बीच में कोई रिक्तता नहीं है। अतः वे समान हैं।
![]()
प्रश्न 5.
\(\frac{1}{17}\) के दशमलव प्रसार में अंकों के पुनरावृत्ति खंड में अंकों की अधिकतम संख्या क्या हो सकती है ? अपने उत्तर की जाँच करने के लिए विभाजन-क्रिया कीजिए।
हल :
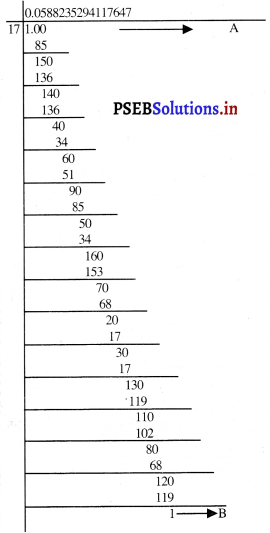
चरण B का शेष चरण A के शेष के समान हैं।
∴ \(\frac{1}{17}\) = 0.0588235294117647……………
= 0.588235294117647 अनवसानी आवर्ती दशमलव
![]()
प्रश्न 6.
\(\frac{p}{q}\) (q ≠ 0), के रूप की परिमेय संख्याओं के अनेक उदाहरण लीजिए, जहाँ p और q पूर्णांक हैं, जिनका 1 के अतिरिक्त अन्य कोई उभयनिष्ठ गुणनखंड नहीं है और जिसका सांत दशमलव निरूपण (प्रसार) है। क्या आप यह अनुमान लगा सकते हैं कि q को कौन-सा गुण अवश्य संतुष्ट करना चाहिए ?
हल :
परिमेय संख्या \(\frac{p}{q}\) (q ≠ 0) को सांत दशमलव रूप में निरूपित करने के लिए यह आवश्यक है कि हर q ऐसा लिया जाए कि 4 के अभाज्य गुणनखंड में केवल 2 के घात, या 5 के घात या दोनों हों।
उदाहरण के लिए
(i) \(\frac{7}{16}\) (q ≠ 0) एक सांत दशमलव है,
क्योंकि 16 = 24
(ii) \(\frac{11}{25}\) एक सांत दशमलव है, क्योंकि
25 = 52
प्रश्न 7.
ऐसी तीन संख्याएँ लिखिए जिनके दशमलव प्रसार अनवसानी अनावर्ती हों।
हल :
जैसा कि हम जानते हैं कि अपरिमेय संख्याओं का दशमलव प्रसार अनवसानी अनावर्ती होता है। इसलिए,
√3 = 1.73205080756…………
\(\frac{1}{\sqrt{5}}\) = 0.44721359549
√10 = 3.16227766016
विद्यार्थियों के स्वयं के उत्तर भी हो सकते हैं। उदाहरण
के लिए :
0.01001000100001………………..
0.202002000200002……………
0.003000300003………………
![]()
प्रश्न 8.
परिमेय संख्याओं \(\frac{5}{7}\) और \(\frac{9}{11}\) के बीच की तीन अलग-अलग अपरिमेय संख्याएँ ज्ञात कीजिए।
हल:
\(\frac{5}{7}\) का दशमलव निरूपण इस प्रकार है :

चरण B का शेष, चरण A के शेष के समान है।
∴ \(\frac{5}{7}=0 . \overline{714285}\)
अब \(\frac{9}{11}\) का दशमलव निरूपण इस प्रकार है :
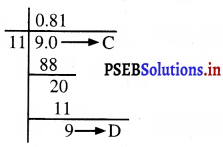
चरण D का शेष, चरण C के शेष के समान है।
∴ \(\frac{9}{11}\) = 0.81
अब हम परिमेय संख्याओं , और – के बीच अपरिमित अनेक अपरिमेय संख्याएँ ज्ञात कर सकते हैं।
इनमें से कोई तीन हैं :
0.75075007500075000075…., 0.767076700767000…और 0.80800800080000……
![]()
प्रश्न 9.
बताइए कि निम्नलिखित संख्याओं में कौनकौन संख्याएँ परिमेय और कौन-कौन संख्याएँ अपरिमेय
(i) \(\sqrt{23}\)
(ii) \(\sqrt{225}\)
(iii) 0.3796
(iv) 7.478478….
(v) 1.101001000100001……
हल :
(i) \(\sqrt{23}\) अपरिमेय संख्या है। क्योंकि 23 एक अभाज्य संख्या है और अभाज्य संख्या एक पूर्ण वर्ग संख्या नहीं है।
(ii) \(\sqrt{225}\) एक परिमेय संख्या है क्योंकि \(\sqrt{225}=\sqrt{15 \times 15}\) = 15.
(iii) 0.3796 एक परिमेय संख्या है क्योंकि यह सांत दशमलव है।
(iv) 7.478478…………. एक परिमेय संख्या है क्योंकि दशमलव प्रसार अनवसानी आवर्ती हैं।
(v) 1.101001000100001………… एक अपरिमेय संख्या है, क्योंकि दशमलव प्रसार अनवसानी अनावर्ती है।
