Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 10 Circles Ex 10.5 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 10 Circles Ex 10.5
Question 1.
In the given figure, A, B and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AGB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.
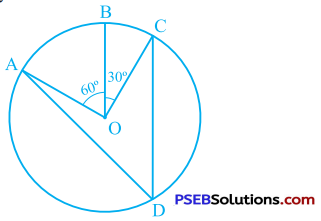
Answer:
∠AOC = ∠AOB + ∠BOC (Adjacent angles)
∴ ∠AQC = 60° + 30°
∴ ∠AOC = 90°
Now, 2 ∠ADC = ∠AOC (Theorem 10.8)
∴ ∠ADC = \(\frac{1}{2}\) ∠AOC
∴ ∠ADC = \(\frac{1}{2}\) × 90°
∴ ∠ADC = 45°
![]()
Question 2.
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Answer:
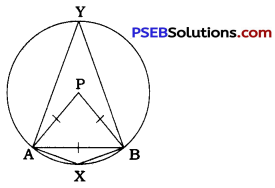
In the circle with centre O, chord AB is equal to radius PA.
∴ In ∆ PAB, PA = PB = AB
∆ PAB is an equilateral triangle.
∴ ∠ APB = 60°
Now, 2∠AYB = ∠APB (Theorem 10.8)
∴ ∠AYB = \(\frac{1}{2}\) ∠APB
= \(\frac{1}{2}\) × 60° = 30°
Quadrilateral AXBY is a cyclic quadrilateral.
∴ ∠X + ∠Y = 180° (Theorem 10.11)
∴ ∠X + 30°= 180°
∴ ∠X = 150°
Thus, the angle subtended by the chord at point X on the minor arc is 150° and the angle subtended by the chord at point Y on the major arc is 30°.
![]()
Question 3.
In the given figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
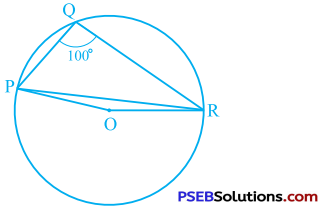
Answer:
Here, reflex angle ∠POR = 2 × ∠PQR (Theorem 10.8)
∴ Reflex angle ∠POR = 2 × 100° = 200°
Now, ∠POR + Reflex angle ∠POR = 360°
∴ ∠POR + 200° = 360°
∴∠POR = 160°
In ∆ OPR. OP = OR (Radii)
∴ ∠OPR = ∠ORP
In ∆ OPR, ∠OPR + ∠ORP + ∠POR = 180°
∴ ∠OPR + ∠OPR + 160° = 180°
∴ 2∠OPR = 20°
∴ ∠OPR = 10°
![]()
Question 4.
In the given figure, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
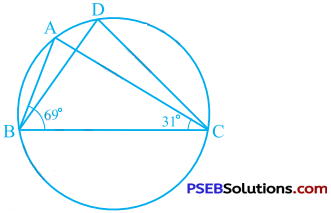
Answer:
In ∆ ABC, ∠ABC + ∠ACB + ∠BAC = 180°
∴ 69° + 31° + ∠BAC = 180°
∴ 100° + ∠BAC = 180°
∴ ∠BAC = 80°
Now, ∠BDC = ∠BAC (Theorem 10.9)
∴ ∠BDC = 80°
Question 5.
In the given figure, A, B, C and D are four s points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
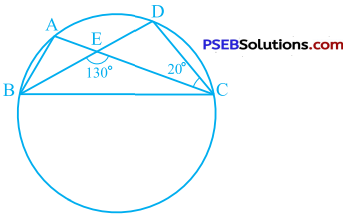
Answer:
In ∆ CDE, ∠BEC is an exterior angle.
∴ ∠BEC = ∠ECD + ∠EDC
∴ 130° = 20° + ∠BDC
∴ ∠BDC = 110°
Now, ∠BAC = ∠BDC (Theorem 10.9)
∴ ∠BAC = 110°
![]()
Question 6.
ABCD is a cyclic quadrilateral Whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
Answer:
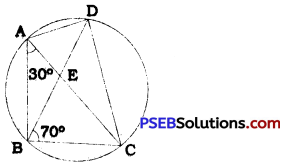
∠DAC = ∠DBC (Theorem 10.9)
∴ ∠DAC = 70°
∠BAD = ∠BAC + ∠DAC (Adjacent angles)
∴ ∠BAD = 30° + 70°
∴ ∠BAD = 100°
In cyclic quadrilateral ABCD,
∠ BAD + ∠BCD = 180° (Theorem 10.11)
∴ 100° + ∠ BCD = 180°
∴ ∠BCD = 80°
In ∆ ABC, if AB = BC, then ∠ BAC = ∠ BCA
∴ 30° = ∠BCA
∴ ∠BCA = 30°
∠BCD = ∠BCA + ∠ACD (Adjacent angles)
∴ 80° = 30° + ∠ACD
∴ ∠ACD = 50°
∴ ∠ECD = 50°
![]()
Question 7.
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Answer:
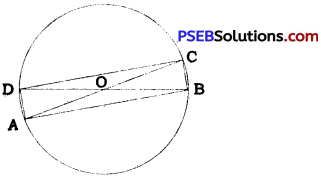
The vertices of cyclic quadrilateral ABCD lie on a circle with centre O and AC and BD are diameters of the circle.
As AC is a diameter, ∠ABC = ∠ADC = 90° (Angle in a semicircle)
As BD is a diameter, ∠BCD = ∠BAD = 90° (Angle in a semicircle)
Thus, all the four angles, ∠BAD, ∠ABC, ∠BCD and ∠ADC of quadrilateral ABCD are right angles.
Hence, quadrilateral ABCD is a rectangle.
Question 8.
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Answer:

In trapezium ABCD, AB || CD and AD = BC.
Draw AM ⊥ CD and BN ⊥ CD, where M and N are points on CD.
In ∆ AMD and ∆ BNC,
∠AMD = ∠BNC (Right angles)
Hypotenuse AD = Hypotenuse BC (Given)
AM = BN (Distance between parallel lines)
∴ By RHS rule, ∆ AMD ≅ ∆ BNC
∴ ∠ADM = ∠BCN
∴ ∠ADC = ∠BCD
Now, AB || CD and AD is their transversal.
∴ ∠BAD + ∠ADC = 180° (Interior angles on the same side of transversal)
∴ ∠ BAD + ∠BCD = 180°
Thus, in quadrilateral ABCD, ∠A + ∠C = 180°.
Hence, ABCD is a cyclic quadrilateral.
![]()
Question 9.
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that ∠ACP = ∠QCD.
Answer:
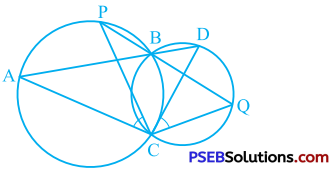
∠ACP and ∠ABP are angles in the same segment.
∴ ∠ACP = ∠ABP (Theorem 10.9) …………… (1)
∠QCD and ∠QBD are angles in the same segment.
∴ ∠QCD = ∠QBD (Theorem 10.9) …………….. (2)
Now, ∠ABP and ∠QBD are vertically opposite angles.
∴ ∠ABP = ∠QBD ………………… (3)
From (1), (2) and (3),
∠ACP = ∠QCD
![]()
Question 10.
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
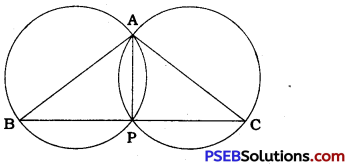
Answer:
Circles are drawn taking sides AB and AC of ∆ ABC as diameters. These circles intersect each other at points A and P.
Draw common chord AP.
Since AB is a diameter, ∠APB is an angle in a semicircle.
∴ ∠APB = 90°
Since, AC is a diameter, ∠APC is an angle in a semicircle.
∴ ∠APC = 90°
Then, ∠APB + ∠APC = 90° + 90° = 180°
∠APB and ∠APC are adjacent angles with common arm AP and their sum is 180°.
∴ ∠APB and ∠APC form a linear pair.
Hence, the point of intersection of the circles with two sides of a triangle as diameters lies on the third side of the triangle.
![]()
Question 11.
ABC and ADC are two right triangles with common hypotenuse AC., Prove that ∠CAD = ∠CBD.
Answer:
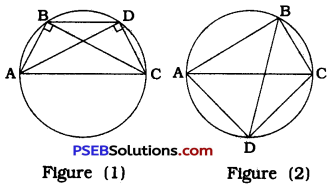
In figure (1), line segment AC subtends equal angles at two points B and D lying on the same side of AC. Hence, by theorem 10.10, all the four points lie on the same circle.
Now, ∠CAD and ∠CBD are angles in the same segment.
∴ ∠CAD = ∠CBD (Theorem 10.9)
In figure (2), in quadrilateral ABCD,
∠B = ∠D = 90°.
∴ ∠B + ∠D = 180°
Hence, ABCD is a cyclic quadrilateral.
Again, ∠CAD and ∠CBD are angles in the same segment.
∴ ∠CAD = ∠CBD (Theorem 10.9)
![]()
Question 12.
Prove that a cyclic parallelogram is a rectangle.
Answer:
Suppose ABCD is a cyclic parallelogram.
ABCD is a cyclic quadrilateral! .
∴ ∠A + ∠C = 180°
and ∠ B + ∠ D = 180° …….. (1)
ABCD is a parallelogram.
∴ ∠A = ∠C and ∠B = ∠D ……….. (2)
From (1) and (2),
∠A = ∠B = ∠C = ∠D = 90°
Thus, all the angles of quadrilateral ABCD are right angles.
Hence, ABCD is a rectangle.
Thus, a cyclic parallelogram is a rectangle.
