Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 10 Circles Ex 10.6 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 10 Circles Ex 10.6
Question 1.
Prove that the line segment joining the centres of two intersecting circles subtends equal angles at the two points of intersection.
Answer:
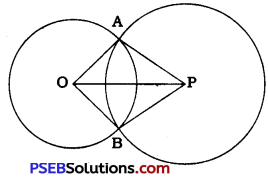
Circles with centres O and P intersect each other at points A and B.
In ∆ OAP and ∆ OBR
OA = OB (Radii of circle with centre O)
PA = PB (Radii of circle with centre P)
OP = OP (Common)
∴ By SSS rule, ∆ OAP = ∆ OBP
∴ ∠OAP = ∠OBP (CPCT)
Thus, OP subtends equal angles at A and B. Hence, the line segment joining the centres of two intersecting circles subtends equal angles at the two points of intersection.
![]()
Question 2.
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
Answer:
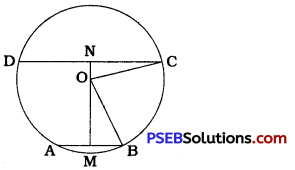
Draw the perpendicular bisector of AB to intersect AB at M and draw the perpendicular bisector of CD to intersect CD at N.
Both these perpendicular bisectors pass through centre O and since AB || CD; M, O and N are collinear points.
Now, MB = \(\frac{1}{2}\)AB = \(\frac{5}{2}\) = 2.5 cm,
CN = \(\frac{1}{2}\)CD = \(\frac{11}{2}\) = 5.5 cm and MN = 6 cm.
Let ON = x cm s
∴ OM = MN – ON = (6 – x) cm
Suppose the radius of the circle is r cm.
∴ OB = OC = r cm
In ∆ OMB, ∠M = 90°
∴OB2 = OM2 + MB2
∴ r2 = (6 – x)2 + (2.5)2
∴ r2 = 36 – 12x + x2 + 6.25 ………….. (1)
In ∆ ONC, ∠N = 90°
∴ OC2 = ON2 + CN2
∴ r2 = (x)2 + (5.5)2
∴ r2 = x2 + 30.25 ………………. (2)
From (1) and (2),
36 – 12x + x2 + 6.25 = x2 + 30.25
∴ – 12x = 30.25 – 6.25 – 36
∴- 12x = – 12
∴x = 1
Now, r2 = x2 + 30.25
∴ r2 = (1)2 + 30.25
∴ r2 = 31.25
∴ r = √31.25 (Approximately 5.6)
Thus, the radius of the circle is √31.25 (approximately 5.6) cm.
Note: If the calculations are carried out in simple fractions, then MB = \(\frac{5}{2}\) cm, CN = \(\frac{11}{2}\) cm and radius is \(\frac{5 \sqrt{5}}{2}\) (approximately 5.6) cm.
![]()
Question 3.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chords is at distance 4 cm from the cehtre, what is the distance of the other chord from the centre?
Answer:
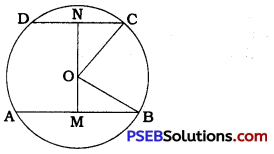
In a circle with centre O, chord AB is parallel to chord CD, AB = 8 cm and CD = 6 cm.
Draw OM ⊥ AB, ON ⊥ CD, radius OB and radius OC.
Then, MB = \(\frac{1}{2}\)AB = \(\frac{1}{2}\) × 8 = 4 cm,
NC = \(\frac{1}{2}\)CD = \(\frac{1}{2}\) × 6 = 3cm and ON = 4cm.
In ∆ ONC, ∠N = 90°
∴ OC2 = ON2 + NC2 = 42 + 32 = 16 + 9 = 25
∴ OC = 5 cm
∴ OB = 5 cm (OB = OC = Radius)
In ∆ OMB, ∠M = 90°
∴ OB2 = OM2 + MB2
∴ 52 = OM2 + 42
∴ 25 = OM2 + 16
∴ OM2 = 9
∴ OM = 3 cm
Thus, the distance of the other chord from the centre is 3 cm.
![]()
Question 4.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Answer:
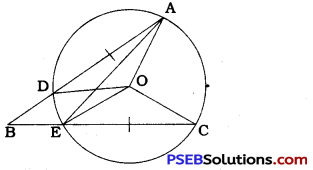
In ∆ ABE, ∠AEC is an exterior angle.
∴ ∠AEC = ∠ABE + ∠BAE
∴ ∠ABE = ∠AEC – ∠BAE
∴ ∠ABC = ∠AEC – ∠DAE ……………. (1)
Now, ∠AEC = \(\frac{1}{2}\) ∠AOC (Theorem 10.8)
and ∠ DAE = \(\frac{1}{2}\) ∠DOE (Theorem 10.8)
Substituting above values in (1),
∠ABC = \(\frac{1}{2}\) ∠AOC – \(\frac{1}{2}\)∠DOE
∴ ∠ABC = \(\frac{1}{2}\) (∠AOC – ∠DOE)
Here, ∠AOC is the angle subtended by chord AC at the centre and ∠DOE is the angle subtended by chord DE at the centre.
Thus, ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Note: There is no need for chords AD and CE to be equal.
![]()
Question 5.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
Answer:
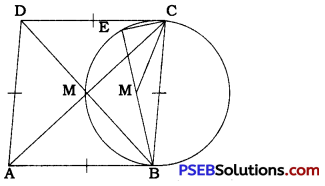
ABCD is a rhombus and its diagonals intersect at M.
∴ ∠BMC is a right angle.
A circle is drawn with diameter BC.
There are three possibilities for point M:
(1) M lies in the interior of the circle,
(2) M lies in the exterior of the circle.
(3) M lies on the circle.
According to (1), if M lies in the interior of the circle, then BM produced will intersect the circle at E. Then, ∠BEC is an angle in a semicircle and hence a right angle, i.e.,
∠MEC = 90°.
In ∆ MEC, ∠ BMC is an exterior angle.
∴ ∠ BMC > ∠ MEC, i.e., ∠ BMC > 90°. In this situation, ∠ BMC is an obtuse angle which contradicts that ∠ BMC = 90°.
Similarly, according to (2), if M lies in the exterior of the circle, then ∠BMC is an acute angle which contradicts that ∠BMC 90°. Thus, possibilities (1) and (2) cannot be true.
Hence, only possibility (3) is true, i.e., M lies on the circle.
Thus, the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
![]()
Question 6.
ABCD is a parallelogram. The circle through A, B and C intersects CD (produced if necessary at) E. Prove that AE = AD.
Answer:
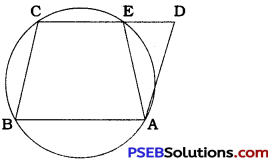
Here, the circle through A, B and C intersects CD at E.
∴ Quadrilateral ABCE is cyclic.
ABCD is a parallelogram.
∴ ∠ABC = ∠ADC
∴ ∠ABC = ∠ADE
In cyclic quadrilateral ABCE,
∠ABC + ∠AEC = 180°
∴ ∠ADE + ∠AEC = 180° ……………… (1)
Moreover, ∠AEC and ∠AED form a linear pair.
∴ ∠AED + ∠AEC = 180° ………………. (2)
From (1) and (2),
∠ADE + ∠AEC = ∠AED + ∠AEC
∴ ∠ ADE = ∠ AED
Thus, in ∆ AED, ∠ADE = ∠AED.
∴ AE = AD (Sides opposite to equal angles)
Note: If the circle intersect CD produced, l then also the result can be proved in similar way.
![]()
Question 7.
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters, (ii) ABCD is a rectangle.
Answer:
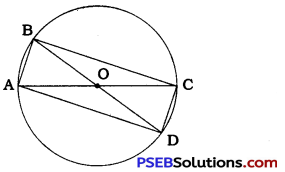
Chords AC and BD of a circle bisect each other at point O.
Hence, the diagonals of quadrilateral ABCD bisect each other.
∴ Quadrilateral ABCD Is a parallelogram.
∴ ∠BAC = ∠ACD (Alternate angles formed by transversal AC of AB || CD)
Moreover, ∠ACD = ∠ABD (Angles in same segment)
∴ ∠BAC = ∠ABD
∴ ∠BAO = ∠ABO
∴ In A OAB, OA = OB.
But, OA = OC and OB = OD
∴ OA = OB = OC = OD
∴ OA + OC = OB + OD
∴ AC = BD
Thus, the diagonals of parallelogram ABCD are equal.
∴ ABCD is a rectangle.
∴ ∠ABC = 90°
Hence, ∠ABC is an angle in a semicircle and AC is a diameter.
Similarly, ∠BAD = 90°.
Hence, ∠BAD is an angle in a semicircle and BD is a diameter.
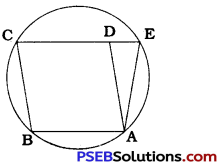
Question 8.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90° – \(\frac{1}{2}\)A, 90° – \(\frac{1}{2}\)B and 90° – \(\frac{1}{2}\)C.
Answer:
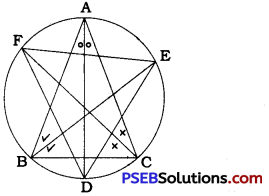
The bisectors of ∠A, ∠B and ∠ C of ∆ ABC intersect the circumcircle of ∆ ABC at D, E and F respectively. .
∠FDE = ∠FDA + ∠EDA (Adjacent angles)
= ∠ FCA + ∠ EBA (Angles in same segment)
= \(\frac{1}{2}\)∠C + \(\frac{1}{2}\)∠B (Bisector of angles in ∆ ABC)
= \(\frac{1}{2}\)(∠ B + ∠ C)
= \(\frac{1}{2}\)(180° – ∠A) [∠A + ∠B + ∠C = 180°)
= 90° – \(\frac{1}{2}\) ∠A
Thus, ∠FDE = 90° – \(\frac{1}{2}\) ∠A.
Similarly, ∠ DEF = 90° – \(\frac{1}{2}\) ∠B and
∠ EFD = 90° – \(\frac{1}{2}\) ∠C.
![]()
Question 9.
Two congruent circles intersect each Other at points A and B. Through A any line segment PAQ is drawn so that P 9 lie-on. , the two circles. Prove that BP = BQ.
Answer:
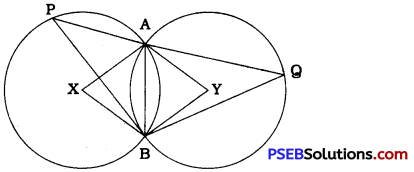
Two congruent circles with centres X and Y intersect at A and B.
Hence, AB is their common chord.
In congruent circles, equal chords subtend equal angles at the centres.
∴ ∠AXB = ∠AYB
In the circle with centre X, ∠AXB = 2∠APB and in the circle with centre Y, ∠AYB = 2∠AQB.
∴ 2∠ APB = 2∠ AQB
∴ ∠APB = ∠AQB
∴ ∠QPB = ∠PQB
Thus, in ∆ BPQ, ∠QPB = ∠PQB
∴ QB = PB (Sides opposite to equal angles)
Hence, BP = BQ.
![]()
Question 10.
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Answer:
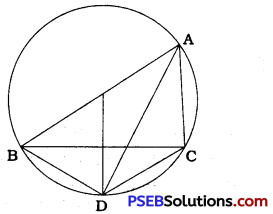
In ∆ ABC, the bisector of ∠A intersects the circumcircle of ∆ ABC at D.
∴∠BAD = ∠CAD
Aso, ∠BAD = ∠BCD and ∠CAD = ∠CBD (Angles in same segment)
∴ ∠BCD = ∠CBD
Thus, in ∆ BCD, ∠BCD = ∠CBD
∴BD = CD (Sides opposite to equal angles)
Thus, point D is equidistant from B and C.
Hence, D is a point on the perpendicular bisector of BC.
Thus, the bisector of ∠ A and the perpendicular bisector of side BC intersect at D and D is a point on the circumcircle of ∆ ABC.
Thus, in ∆ ABC, if the angle bisector of ∠A and the perpendicular bisector of side BC intersect, they intersect on the circumcircle of ∆ ABC.
Note: In ∆ ABC, if AB = AC, then the bisector of ∠A and the perpendicular bisector of side BC will coincide , and would not intersect in a single point.
