PSEB 9th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.2

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.2

जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}\) लीजिए।

प्रश्न 1.
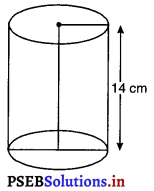
ऊँचाई 14 cm वाले एक लंब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 88 cm² है। बेलन के आधार का व्यास ज्ञात कीजिए।
हल :
मान लीजिए लंब वृत्तीय बेलन के आधार की त्रिज्या = r cm
बेलन की ऊँचाई = h = 14 cm
बेलन का वक्र पृष्ठीय क्षेत्रफल = 88 cm²
⇒ 2πrh = 88
⇒ 2× \(\frac{22}{7}\) × r × 14 = 88

⇒ r = 88 × \(\frac{7}{22}\) × \(\frac{1}{14}\) × \(\frac{1}{2}\)
⇒ r = 1 cm
बेलन के आधार का व्यास = 2r
= 2 × 1
= 2 cm

प्रश्न 2.
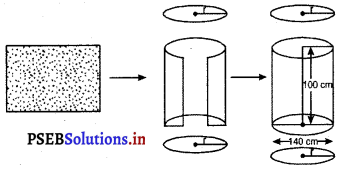
धातु की चादर से 1 m ऊँची और 140 cm व्यास के आधार वाली एक बंद बेलनाकार टंकी बनाई जानी है। इस कार्य के लिए कितने वर्ग मीटर चादर की आवश्यकता होगी ?

हल :
मान लीजिए बेलनाकार टंकी के आधार की त्रिज्या = r cm
∴ व्यास = 2r = 140 cm
⇒ r = \(\frac{140}{2}\) cm
⇒ r = 70 cm
⇒ r = \(\frac{70}{100}\)
⇒ r = 0.7 m
बेलन की ऊँचाई = h = 1m
बेलन का कुल पृष्ठीय क्षेत्रफल = 2πr (r + h)
= 2 × \(\frac{22}{7}\) × 0.7(0.7+1)
= 2 × 22 × 0.1 × 1.7
= 7.48 m²
अतः, बंद बेलनकारार टंकी बनाने के लिए 7.48 m² चादर की आवश्यकता है।

प्रश्न 3.
धातु का एक पाइप 77 cm लंबा है। इसके एक अनुप्रस्थकाट का आंतरिक व्यास 4 cm है और बाहरी व्यास 4.4 cm है ( देखिए आकृति)।
(i) आंतरिक वक्र पृष्ठीय क्षेत्रफल
(ii) बाहरी वक्र पृष्ठीय क्षेत्रफल
(iii) कुल पृष्ठीय क्षेत्रफल

हल :

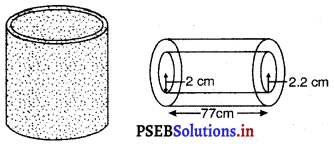
पाइप की लंबाई = 77 cm
(i) अनुप्रस्थ काट का आंतरिक व्यास = 4 cm
∴ अनुप्रस्थ काट की आंतरिक त्रिज्या r = \(\frac{4}{2}\)
= 2 cm
क्योंकि पाइप बेलनाकार है,
∴ आंतरिक वक्र पृष्ठीय क्षेत्रफल = 2πrh
[∵ पइप की लंबाई = ऊँचाई]
= 2 × \(\frac{22}{7}\) × 2 × 77
= 2 × 22 × 2 × 11
= 968 cm²

(ii) पाइप की लंबाई = 77 cm
पाइप का बाहरी व्यास = 4.4 cm
पाइप की बाहरी त्रिज्या R = \(\frac{4.4}{2}\) = 2.2 cm
∴ बेलन का बाहरी वक्र पृष्ठीय क्षेत्रफल
= 2πrh
= 2 × \(\frac{22}{7}\) × 2.2 × 77
= \(\frac{44}{7}\) × \(\frac{22}{10}\) × 77
= 44 × \(\frac{22}{10}\) × 11
= 1064.8 cm²

(iii) अब पाइप के दोनों अंत सिरों में प्रत्येक सिरे पर 2 cm और 2.2 cm त्रिज्याओं के वृत्त हैं,
∴ पाइप के दोनों सिरों का क्षेत्रफल = 2
(बाहरी वृत्त का क्षेत्रफल – आंतरिक वृत्त का क्षेत्रफल)
= 2 (πR² – πr²)
= 2π(R² – r²)
= 2 × 2 [(2.2)² – (2)²]
= \(\frac{44}{7}\) [4.84 – 4]
= \(\frac{44}{7}\) × 0.84
= 5.28 cm²
∴ पाइप का कुल पृष्ठीय क्षेत्रफल = आंतरिक वक्र पृष्टीय क्षेत्रफल + बाहरी वक्र पृष्ठीय क्षेत्रफल + दो वृत्तीय सिरों का क्षेत्रफल
= 968 cm² + 1064.8 cm² + 5.28 cm²
= 2038.08 cm²

प्रश्न 4.
एक रोलर (roller) का व्यास 84 cm है और लंबाई 120 cm है। एक खेल के मैदान को एक बार समतल करने के लिए 500 चक्कर लगाने पड़ते हैं। खेल के मैदान का m² में क्षेत्रफल ज्ञात कीजिए।
हल :
रोलर का व्यास = 84 cm

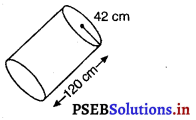
रोलर की त्रिज्या r = \(\frac{84}{2}\) = 42 cm
रोलर की लंबाई l = 120 cm
∵ रोलर बेलन के आकार का है
∴ रोलर का वक्र पृष्ठीय क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल
= 2π rh (l = h)
= 2 × \(\frac{22}{7}\)42 × 120
= 31680 cm²
\(\frac{31680}{100 \times 100} \mathrm{~m}^2\) = 3.1680 m²
अब रोलर द्वारा एक चक्कर में समतल किया गया क्षेत्रफल = 3.1680 m²
∴ रोलर द्वारा 500 चक्करों में समतल किया गया क्षेत्रफल = 500 × 3.1680
= 1584.0000
= 1584 m²
खेल के मैदान का क्षेत्रफल = रोलर द्वारा 500 चक्करों में समतल किया गया क्षेत्रफल
= 1584 m²

प्रश्न 5.
किसी बेलनाकार स्तंभ का व्यास 50 cm है और ऊँचाई 3.5 cm है। 12.50 रुपए प्रति m² की दर से इस स्तंभ के वक्र पृष्ठ पर पेंट कराने का व्यय ज्ञात कीजिए।
हल :
स्तंभ का व्यास = 50 cm
∴ स्तंभ की त्रिज्या = \(\frac{50}{2}\) = 25 cm = \(\frac{25}{100}\)
= \(\frac{1}{4}\) m
स्तंभ की ऊँचाई = 3.5 m
स्तंभ का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 × \(\frac{22}{7}\) × \(\frac{1}{4}\) × 3.5
= 2 × \(\frac{22}{7}\) × \(\frac{1}{4}\) × \(\frac{35}{10}\) = \(\frac{11}{2}\) m²
1 m² पेंट कराने का व्यय = 12.50 रु

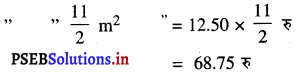
प्रश्न 6.
एक लंब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 4.4 m² है। यदि बेलन के आधार की त्रिज्या 0.7 m है, तो उसकी ऊँचाई ज्ञात कीजिए।
हल :
बेलन का वक्र पृष्ठीय क्षेत्रफल = 4.4 m²
बेलन की त्रिज्या r = 0.7 m
मान लीजिए बेलन की ऊँचाई = h
∴ 2πrh = 4.4
या, 2 × \(\frac{22}{7}\) × 0.7 × h = 4.4
या, 44 × 0.1 × h = 4.4
या, 44 × \(\frac{1}{210}\) × h = \(\frac{44}{10}\)
या, h = \(\frac{44}{10} \times \frac{10}{1} \times \frac{1}{44}\) = 1 m

प्रश्न 7.
किसी वृत्ताकार कुएँ का आंतरिक व्यास 3.5 m है और यह 10 m गहरा है। ज्ञात कीजिए:
(i) आंतरिक वक्र पृष्ठीय क्षेत्रफल
(ii) 40 रुपए प्रति m² की दर से इसके वक्र पृष्ठ पर प्लास्टर कराने का व्यय।
हल :
वृत्ताकार कुएँ का आंतरिक व्यास = 3.5 m
वृत्ताकार कुएँ की त्रिज्या = \(\frac{3.5}{2}\) = 1.75 m
कुएँ की गहराई = 10 m
कुएँ का आकार बेलनाकार है।
भाग (i) के लिए, ∴ कुएँ की आंतरिक वक्र पृष्ठीय
= 2πrh [यहाँ गहराई = कुएँ की ऊँचाई]

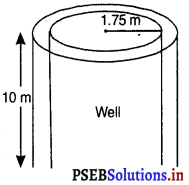
= 2× \(\frac{22}{7}\) × 1.75 × 10 m²
= 2 × \(\frac{22}{7}\) × \(\frac{175}{100}\) × 10 m²
= 110 m²
भाग (ii), के लिए 1m² पर प्लास्टर कराने का व्यय = 40 रु०
100 m² पर प्लस्टर कराने का व्यय
40 × 110 रु० = 4400 रु०

प्रश्न 8.
गरम पानी द्वारा गरम रखने वाले एक संयंत्र में 28 m लंबाई और 5 cm व्यास वाला एक बेलनाकार पाइप है। इस संयत्र में गर्मी देने वाला कुल कितना पृष्ठ है ?
हल :
मान लीजिए बेलनकार पाइप की लंबाई (अर्थात् ऊँचाई) = h
∴ h = 28 m
और बेलनाकार पाइप की त्रिज्या = r ,
∴ 2r = 5 cm
⇒ r = \(\frac{5}{2}\) cm
गर्मी देने वाला बेलनाकार
∴ पाइप का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 × \(\frac{22}{7}\) × \(\frac{5}{2}\) × 2800
= 44000 cm²
= \(\frac{44000}{10000}\) m²
[∵ 1 cm = \(\frac{1}{100}\) m
∴ 1 cm² = \(\frac{1}{10000}\) m²]
= 4.4 m²

प्रश्न 9.
ज्ञात कीजिए :
(i) एक बेलनाकार पेट्रोल की बंद टंकी का पाव या वक्र पृष्ठीय क्षेत्रफल, जिसका व्यास 4.2 m है और ऊँचाई 4.5 m है।
(ii) इस टंकी को बनाने में कुल कितना इस्पात (steel) लगा होगा, यदि कुल इस्पात का \(\frac{1}{2}\) भाग बनाने में नष्ट हो गया है ?
हल :
(i) मान लीजिए बेलनाकार पेट्रोल की टंकी की त्रिज्या = r
∴ व्यास; 2r = 4.2 m
⇒ r = 2.1 m
टंकी की ऊँचाई, h = 4.5 m
पेट्रोल की टंकी का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 × \(\frac{22}{7}\) × 2.1 × 1.45 m²
= 59.4 m²

(ii) मान लीजिए टंकी बनाने में प्रयुक्त हुआ इस्पात का वास्तविक क्षेत्रफल x m² है।
क्योंकि कुल इस्पात का \(\frac{1}{12}\) भाग बनाने में नष्ट हुआ, टंकी को बनाने में लगे इस्पात का क्षेत्रफल
= x – \(\frac{1}{12}\)x
= \(\frac{11}{12}\)x
\(\frac{11}{12}\)x = 59.4 m²
⇒ x = 59.4 × \(\frac{12}{11}\)
⇒ x = 64.8 m²
अतः, टंकी को बनाने में लगा स्टील 64.8 m² है।

प्रश्न 10.
आकृति में, आप एक लैंपशेड का फ्रेम देख रहे हैं। इसे एक सजावटी कपड़े से ढका जाना है। इस फ्रेम के आधार का व्यास 20 cm है और ऊँचाई 30 cm है। फ्रेम के ऊपर और नीचे मोड़ने के लिए दोनों ओर 2.5 cm अतिरिक्त कपड़ा भी छोड़ा जाना है। ज्ञात कीजिए कि लैंपशेड को ढकने के लिए कुल कितने कपड़े की आवश्यकता होगी।

हल :

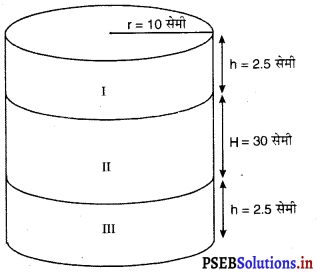
फ्रेम की ऊँचाई, H = 30 सेमी
ऊपर और नीचे मोड़ने वाले प्रत्येक कपड़े की ऊँचाई
h = 2.5 सेमी
मान लीजिए प्रत्येक भाग की त्रिज्या = r
व्यास, 2r = 20 cm
⇒ r = \(\frac{20}{2}\) cm
लैंपशेड ढकने के लिए आवश्यक कंपड़ा = बेलन I के वक्र पृष्ठ का क्षे० + बेलन II के वक्र पृष्ठ का क्षे० + बेलन III के वक्र पृष्ठ का क्षे०
= 2πrh + 2πrH + 2πrh
= 2πr (h + H + h)
= 2πr (H + 2h)
= 2 × \(\frac{22}{7}\) × 10 (30 + 2 × 2.5) सेमी²
= \(\frac{440}{7}\) × 35
= 440 × 5
= 2200 सेमी²

प्रश्न 11.
किसी विदयालय के विदयार्थियों से एक आधार वाले बेलनाकार कलमदानों को गत्ते से बनाने और सजाने की प्रतियोगिता में भाग लेने के लिए कहा गया। प्रत्येक कलमदान को 3 cm त्रिज्या और 10.5 cm ऊँचाई का होना था। विद्यालय को इसके लिए प्रतिभागियों को गत्ता देना था। यदि इसमें 35 प्रतिभागी थे, तो विद्यालय को कितना गत्ता खरीदना पड़ा होगा ?
हल :
मान लीजिए बेलनकार कलमदान की त्रिज्या = r
∴ r = 3 cm
और बेलनाकार कलमदान की ऊँचाई = h एक कलमदान के लिए वांछित गत्ता
∴ h = 10.5 cm
कलमदान का वक्र पृष्ठीय क्षेत्रफल + वृत्ताकार आधार का क्षेत्रफल
= 2πrh + πr²
= πr (2h + r)
= \(\frac{22}{7}\) × 3 (2 × 10.5 + 3)
= \(\frac{22}{7}\) × 3 (21 + 3)
= \(\frac{22}{7}\) × 3 × 24
= 226.28 cm²
अब, एक कलमदान बनाने के के लिए वांछित गत्ता = 226.28 cm²
∴ 35 कलमदान बनाने के लिए वांछित गत्ता
= (226.28 × 35) cm²
= 7919.8 cm²
= 7620 cm² (लगभग)