Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.3 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.3
जब तक अन्यथा न कहा जाए π = \(\frac{22}{7}\) लीजिए।
प्रश्न 1.
एक शंकु के आधार पर व्यास 10.5 cm है और इसकी तिर्यक ऊँचाई 10 cm है। इसका वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :
मान लीजिए कि वृत्ताकार आधार की त्रिज्या = r cm
∴ व्यास ; 2r = 10.5 cm
⇒ r = \(\frac{10.5}{2}\)
⇒ r = \(\frac{105}{20}\)
⇒ r = \(\frac{21}{4}\)
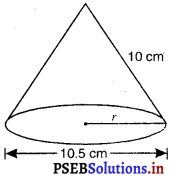
शंकु की तिर्यक ऊँचाई = l = 10 cm
इसलिए, शंकु का वक्र पृष्ठीय क्षेत्रफल = πrl
= \(\frac{22}{7}\) × \(\frac{21}{4}\) × 10
= 165 cm2
प्रश्न 2.
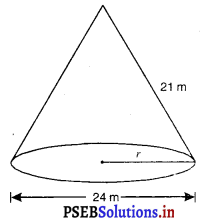
एक शंकु का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए, जिसकी तिर्यक ऊँचाई 21 m है और आधार का व्यास 24 m है।
हल :
शंकु की तिर्यक ऊँचाई l = 21 m
शंकु का व्यास = 24 m
शंकु की त्रिज्या, r = \(\frac{24}{2}\) = 12 m
शंकु का कुल पृष्ठीय क्षेत्रफल = πrl + πr2
= πr (l + r)
= \(\frac{22}{7}\) × 12 (21 + 12) m2
= \(\frac{264}{7}\) × 33 = 1244.57 m2
![]()
प्रश्न 3.
एक शंकु का वक्र पृष्ठीय क्षेत्रफल 380 cm2 है और इसकी तिर्यक ऊँचाई 14 cm है। ज्ञात कीजिए :
(i) आधार की त्रिज्या
(ii) शंकु का कुल पृष्ठीय क्षेत्रफल
हल :
(i) मान लीजिए शंकु के वृत्तीकार आधार की त्रिज्या = r
तिर्यक ऊँचाई ; l = 14 cm
शंकु का वक्र पृष्ठीय क्षेत्रफल = 308 cm2 (दिया है)
⇒ πrl = 308
⇒ \(\frac{22}{7}\) × r × 14 = 308
⇒ r = 308 × \(\frac{7}{22}\) × \(\frac{1}{14}\)
⇒ r = 7 cm
(ii) शंकु का कुल पृष्ठीय क्षेत्रफल = शंकु का वक्र पृष्ठीय क्षेत्रफल + शंकु के वृत्तीय आधार का क्षेत्रफल
= 308 + πr2
= 308 + \(\frac{22}{7}\) × 72
= 308 + 22 × 7
= 308 + 154
= 462 cm2
प्रश्न 4.
शंकु के आकार का एक तंबू 10 m ऊँचा है उसके आधार की त्रिज्या 24 m है। ज्ञात कीजिए:
(i) तंबू की तिर्यक ऊँचाई
(ii) तंबू में लगे केनवास (canvas) की लागत, यदि 1 m2 केनवास की लागत 70 रुपए है।
हल :
शंक्वाकार तंबू की ऊँचाई h = 10 m
शंक्वाकार तंबू की त्रिज्या ; r = 24 m
(i) तंबू की तिर्यक ऊँचाई ; l = \(\sqrt{r^2+h^2}\)
= \(\sqrt{(24)^2+(10)^2}\)
= \(\sqrt{576+100}\)
= \(\sqrt{676}\)
= 26 m
भाग (ii) के लिए, तंबू को बनाने में लगा केनवास = तंबू का वक्र पृष्ठीय क्षेत्रफल
= πrl
= \(\frac{22}{7}\) × 24 × 26 = \(\frac{13728}{7}\) m2
\(\frac{13728}{7}\) m2 केनवास का मूल्य
= 70 × \(\frac{13728}{7}\) रु
= 137280 रु
![]()
प्रश्न 5.
8 m ऊँचाई और आधार की त्रिज्या 6 m वाले एक शंकु के आकार का तंबू बनाने में 3 m चौड़े तिरपाल की कितनी लंबाई लगेगी? यह मान कर चलिए कि इसकी सिलाई और कटाई में 20 cm तिरपाल अतिरिक्त लगेगा। (π = 3.14 का प्रयोग कीजिए)
हल :
तंबू की ऊँचाई ; h = 8 m
तंबू की त्रिज्या ; r = 6 m
तंबू की तिर्यक ऊँचाई ; l = \(\sqrt{r^2+h^2}\)
= \(\sqrt{(6)^2+(8)^2}\)
= \(\sqrt{36+64}\)
= \(\sqrt{100}\)
= 10 m
तिरपाल का क्षेत्रफल = तंबू का वृक्र पृष्ठीय क्षेत्रफल
= πrl = 3.14 × 6 × 10 = 188.4 m2
तिरपाल की चौड़ाई = 3 m
मान लीजिए तिरपाल की लंबाई = L
तिरपाल का क्षेत्रफल = लंबाई × चौड़ाई
= L × 3 = 3L
3L = 188.4 [∵ क्षेत्रफल = 188.4 m2]
L = \(\frac{188.4}{3}\) = 62.8 m
सिलाई और कटाई में लगी तिरपाल की अतिरिक्त लंबाई 20 cm है।
अर्थात् 0.2 m [∵ 1 cm = \(\frac{1}{100}\) m]
इसलिए तंबू बनाने में लगी तिरपाल की कुल लंबाई (62.8 + 0.2) m = 63 m
प्रश्न 6.
शंकु के आधार की एक गुंबज की तिर्यक ऊँचाई और आधार व्यास क्रमशः 25 m और 14 m हैं। इसकी वक्र पृष्ठ पर 210 रुपए प्रति 100 m2 की दर से सफेदी कराने का व्यय ज्ञात कीजिए।
हल :
शंक्वाकार गुंबज की तिर्यक ऊँचाई l = 25 m
शंक्वाकार गुंबज के आधार का व्यास = 14 m
शंक्वाकार गुंबज की त्रिज्या r = \(\frac{14}{2}\) = 7m
गुंबज का वक्र पृष्ठीय क्षेत्रफल = πrl
= \(\frac{22}{7}\) × 7 × 25 = 550 m2
100 m2 पर सफेदी कराने का व्यय = 210 रु
1 m2 पर सफेदी कराने का व्यय = \(\frac{210}{100}\) रु
550 m2 पर सफेदी कराने का व्यय = \(\frac{210}{100}\) × 550 रु
= 1155 रु
![]()
प्रश्न 7.
एक जोकर की टोपी एक शंकु के आकार की है, जिसके आधार की त्रिज्या 7 cm और ऊँचाई 24 cm है। इसी प्रकार की 10 टोपियाँ बनाने के लिए आवश्यक गत्ते का क्षेत्रफल ज्ञात कीजिए।
हल :
टोपी के आधार की त्रिज्या r = 7 cm
टोपी की ऊँचाई ; h = 24 cm
टोपी शंकु के आकार की है।
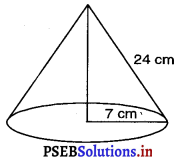
तिर्यक ऊँचाई ; l = \(\sqrt{r^2+h^2}\)
= \(\sqrt{(7)^2+(24)^2}\)
= \(\sqrt{49+576}\) = \(\sqrt{625}\) = 25 cm
एक टोपी बनाने में लगे गत्ते का क्षेत्रफल = शंकु का वक्र पृष्ठीय क्षेत्रफल
= πrl
= \(\frac{22}{7}\) × 7 × 25 = 550 cm2
∴ 10 टोपियाँ बनाने में लगे गत्ते का क्षेत्रफल = 10 × 550 = 5500 cm2
प्रश्न 8.
किसी बस स्टाप को पुराने गत्ते से बने 50 खोखले शंकुओं द्वारा सड़क से अलग किया हुआ है। प्रत्येक शंकु के आधार का व्यास 40 cm है और ऊँचाई 1 m है। यदि इन शंकुओं की बाहरी पृष्ठों को पेंट करवाना है और पेट की दर 12 रुपए प्रति m2 है, तो इनको पेंट कराने में कितनी लागत आएगी ?
(π = 3.14, और \(\sqrt{1.04}\) = 1.02 का प्रयोग कीजिए)
हल :
मान लीजिए वृत्तीकार आधार की त्रिज्या = r
∴ व्यास ; 2r = 40
⇒ r = \(\frac{40}{2}\)
⇒ r = 20 m
⇒ r = \(\frac{20}{100}\) m
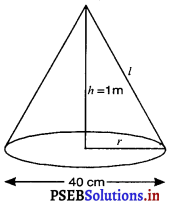
शंकु की ऊँचाई, h = 1 m
तिर्यक ऊँचाई, l = \(\sqrt{r^2+h^2}\)
= \(\sqrt{(0.2)^2+(1)^2}\)
l = \(\sqrt{0.04+1}\)
l = \(\sqrt{1.04}\)
शंकु का वक्र पृष्ठीय क्षेत्रफल = πrl
= 3.14 × 0.2 × \(\sqrt{1.04}\)
= 3.14 × 0.2 × 1.02
= 0.64056 m2
1m2 शंकु को पेंट कराने की लागत = 12 रु
0.64056 m2 शंकु को पेंट कराने की लागत = (12 × 0.64056) रु
= 7.68672 रु
एक शंकू को पेंट कराने की लागत = 7.68672 रु
ऐसे 50 शंकु को पेंट कराने की लागत = 50 × 7.68672 रु
= 384.34 रु (लगभग)
